15.2: Vibration-Rotation Transitions
- Page ID
- 60587
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When the initial and final electronic states are identical, but the respective vibrational and rotational states are not, one is dealing with transitions between vibration-rotation states of the molecule. These transitions are studied in infrared (IR) spectroscopy using light of energy in the 30 cm\(^{-1} \text{ (far IR) to 5000 cm}^{-1}\) range. The electric dipole matrix element analysis still begins with the electronic dipole moment integral \(\langle \psi_{ei} | \mu | \psi_{ei} \rangle = \mu (\textbf{R}),\) but the integration over internal vibrational coordinates no longer produces the vibrationally averaged dipole moment. Instead one forms the vibrational transition dipole integral:
\[ \langle \chi_{vf} | \mu (\textbf{R} ) | \chi_{vi} \rangle = \mu_{f,i} \nonumber \]
between the initial \( \chi_i \text{ and final } \chi_f \) vibrational states.
The Dipole Moment Derivatives
Expressing \(\mu ( \textbf{R} )\) in a power series expansion about the equilibrium bond length position (denoted \(\textbf{R}_e\) collectively and \(R_{a,e}\) individually):
\[ \mu ( \textbf{R} ) = \mu( \textbf{R}_e ) + \sum\limits_a \dfrac{\partial \mu}{\partial R_a}(R_a - R_{a,e}) + ..., \nonumber \]
substituting into the \( \langle\chi_{vf} | \mu ( \textbf{R} ) | \chi_{vi} \rangle \) integral, and using the fact that \(\chi_i \text{ and } \chi_f\) are orthogonal (because they are eigenfunctions of vibrational motion on the same electronic surface and hence of the same vibrational Hamiltonian), one obtains:
\[ \langle \chi_{vf} | \mu ( \textbf{R} ) | \chi_{vi} \rangle = \mu ( \textbf{R}_e ) \langle \chi_{vf} | \chi_{vi} \rangle + \sum\limits_a \dfrac{\partial \mu}{\partial \textbf{R}_a} \langle \chi_{vf} | (R_a - R_{a,e}) | \chi_{vi} \rangle + ... \nonumber \]
\[ = \sum\limits_a \left( \dfrac{\partial \mu}{\partial \textbf{R}_a}\right) \langle\chi_{vf} | (\textbf{R}_a - \textbf{R}_{a,e}) | \chi_{vi} \rangle + ... . \nonumber \]
This result can be interpreted as follows:
- Each independent vibrational mode of the molecule contributes to the \( \mu_{f,i} \) vector an amount equal to \( \left( \dfrac{\partial \mu}{\partial \textbf{R}_a} \right) \langle \chi_{vf} | (\textbf{R}_a - \textbf{R}_{a,e}) | \chi_{vi} \rangle + ... . \)
- Each such contribution contains one part \( \left( \dfrac{\partial \mu}{\partial \textbf{R}_a} \right) \) that depends on how the molecule's dipole moment function varies with vibration along that particular mode (labeled a),
- and a second part \( \langle\chi_{vf} | ( \textbf{R}_a - \textbf{R}_{a,e} ) | \chi_{vi} \rangle \) that depends on the character of the initial and final vibrational wavefunctions.
If the vibration does not produce a modulation of the dipole moment (e.g., as with the symmetric stretch vibration of the \(CO_2\) molecule), its infrared intensity vanishes because \( \left( \dfrac{\partial \mu}{\partial \textbf{R}_a} \right) = 0. \) One says that such transitions are infrared "inactive".
Selection Rules on v in the Harmonic Approximation
If the vibrational functions are described within the harmonic oscillator approximation, it can be shown that the \( \langle\chi_{vf} | ( \textbf{R}_a - \textbf{R}_{a,e} ) | \chi_{vi}\rangle \) integrals vanish unless vf = vi +1 , vi -1 (and that these integrals are proportional to \(\sqrt{(vi +1)} \text{ and } \sqrt{(vi)}\) in the respective cases). Even when \(\chi_{vf} \text{ and } \chi_{vi}\) are rather non-harmonic, it turns out that such \(\Delta v = \pm 1\) transitions have the largest \( \langle\chi_{vf} | (\textbf{R}_a - \textbf{R}_{a,e}) | \chi_{vi} \rangle \) integrals and therefore the highest infrared intensities. For these reasons, transitions that correspond to \(\Delta v = \pm 1\) are called "fundamental"; those with \(\Delta v = \pm 2\) are called "first overtone" transitions.
In summary then, vibrations for which the molecule's dipole moment is modulated as the vibration occurs (i.e., for which \(\left( \frac{\partial \mu}{\partial \textbf{R}_a}\right)\) is non-zero) and for which \(\Delta v = \pm 1\) tend to have large infrared intensities; overtones of such vibrations tend to have smaller intensities, and those for which \( \left( \frac{\partial \mu}{\partial \textbf{R}_a} \right) = 0 \) have no intensity.
Rotational Selection Rules
The result of all of the vibrational modes' contributions to
\[ \sum\limits_a \left( \frac{\partial \mu}{\partial \textbf{R}_a} \right) \langle \chi_{vf} | (\textbf{R}_a - \textbf{R}_{a,e}) | \chi_{vi} \rangle \nonumber \]
is a vector \(\mu_{trans}\) that is termed the vibrational "transition dipole" moment. This is a vector with components along, in principle, all three of the internal axes of the molecule. For each particular vibrational transition (i.e., each particular \(\chi_i \text{ and } \chi_f\) ) its orientation in space depends only on the orientation of the molecule; it is thus said to be locked to the molecule's coordinate frame. As such, its orientation relative to the lab-fixed coordinates (which is needed to effect a derivation of rotational selection rules as was done earlier in this Chapter) can be described much as was done above for the vibrationally averaged dipole moment that arises in purely rotational transitions. There are, however, important differences in detail. In particular,
- For a linear molecule \(\mu_{trans}\) can have components either along (e.g., when stretching vibrations are excited; these cases are denoted \(\sigma\)-cases) or perpendicular to (e.g., when bending vibrations are excited; they are denoted \(\pi\) cases) the molecule's axis.
- For symmetric top species, \(\mu_{trans}\) need not lie along the molecule's symmetry axis; it can have components either along or perpendicular to this axis.
- For spherical tops, \(\mu_{trans}\) will vanish whenever the vibration does not induce a dipole moment in the molecule. Vibrations such as the totally symmetric \(a_1\) C-H stretching motion in CH\(_4\) do not induce a dipole moment, and are thus infrared inactive; non-totally-symmetric vibrations can also be inactive if they induce no dipole moment.
As a result of the above considerations, the angular integrals
\[ \langle \phi_{ir} | \mu_{trans} | \phi_{fr} \rangle = \int \text{D}_{\text{L, M, K}}(\theta ,\phi , \chi) \mu_{trans} \textbf{D}^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
that determine the rotational selection rules appropriate to vibrational transitions produce similar, but not identical, results as in the purely rotational transition case.
The derivation of these selection rules proceeds as before, with the following additional considerations. The transition dipole moment's \( \mu_{trans}\) components along the labfixed axes must be related to its molecule-fixed coordinates (that are determined by the nature of the vibrational transition as discussed above). This transformation, as given in Zare's text, reads as follows:
\[ (\mu_{trans})_m = \sum\limits_k \textbf{D}^{\text{*}}_{\text{l, m, k}}(\theta , \phi , \chi )(\mu_{trans})_k \nonumber \]
where \((\mu_{trans})_m \) with m = 1, 0, -1 refer to the components along the lab-fixed (X, Y, Z) axes and \((\mu_{trans})_k\) with k = 1, 0, -1 refer to the components along the molecule- fixed (a, b, c) axes.
This relationship, when used, for example, in the symmetric or spherical top E1 integral:
\[ \langle \phi_{ir} | \mu_{trans} | \phi_{fr} \rangle = \int \text{D}_{\text{L,M,K}}(\theta , \phi , \chi )\mu_{trans} \textbf{D}^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
gives rise to products of 3-j symbols of the form:
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{K' k -K}} \right). \nonumber \]
The product of these 3-j symbols is nonvanishing only under certain conditions that provide the rotational selection rules applicable to vibrational lines of symmetric and spherical top molecules.
Both 3-j symbols will vanish unless
L = L' +1, L', or L'-1.
In the special case in which L = L' =0 (and hence with M = M' =0 = K = K', which means that m = 0 = k), these 3-j symbols again vanish. Therefore, transitions with
L = L' =0
are again forbidden. As usual, the fact that the lab-fixed quantum number m can range over m = 1, 0, -1, requires that
M = M' + 1, M', M'-1.
The selection rules for \(\Delta \textbf{K}\) depend on the nature of the vibrational transition, in particular, on the component of \(\mu_{trans}\) along the molecule-fixed axes. For the second 3-j symbol to not vanish, one must have
K = K' + k,
where k = 0, 1, and -1 refer to these molecule-fixed components of the transition dipole. Depending on the nature of the transition, various k values contribute.
Symmetric Tops
In a symmetric top molecule such as \(NH_3\), if the transition dipole lies along the molecule's symmetry axis, only k = 0 contributes. Such vibrations preserve the molecule's symmetry relative to this symmetry axis (e.g. the totally symmetric N-H stretching mode in \(NH_3\)). The additional selection rule \(\Delta K = 0\) is thus obtained. Moreover, for K = K' = 0, all transitions with \(\Delta L = 0\) vanish because the second 3-j symbol vanishes. In summary, one has:
\( \Delta K = 0; \Delta M = \pm 1, 0; \Delta L = \pm 1,0\) (but L = L' = 0 is forbidden and all \(\Delta L = 0\) are forbidden for K = K' = 0)
for symmetric tops with vibrations whose transition dipole lies along the symmetry axis.
If the transition dipole lies perpendicular to the symmetry axis, only k = ±1 contribute. In this case, one finds
\( \Delta K = \pm 1; \Delta M = \pm 1, 0; \Delta L = \pm 1, 0 \) (neither L = L' = 0 nor K = K' = 0 can occur for such transitions, so there are no additional constraints).
Linear Molecules
When the above analysis is applied to a diatomic species such as HCl, only k = 0 is present since the only vibration present in such a molecule is the bond stretching vibration, which has \(\sigma\) symmetry. Moreover, the rotational functions are spherical harmonics (which can be viewed as \(\textbf{D}^{\text{*}}_{\text{L',M',K'}}(\theta , \phi ,\chi )\) functions with K' = 0), so the K and K' quantum numbers are identically zero. As a result, the product of 3-j symbols
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' n -M}} \right) \left( \dfrac{\text{L' 1 L}}{K' k -K} \right) \nonumber \]
reduces to
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 0}} \right) \nonumber \]
which will vanish unless
\[ \text{ L = L' + 1, L' - 1, } \nonumber \]
but not L = L' (since parity then causes the second 3-j symbol to vanish), and
\[ \text{ M = M' + 1, M', M' - 1. } \nonumber \]
The L = L' +1 transitions are termed R-branch absorptions and those obeying L = L' -1 are called P-branch transitions. Hence, the selection rules
\[ \Delta M = \pm 1, 0; \Delta L = \pm 1 \nonumber \]
are identical to those for purely rotational transitions.
When applied to linear polyatomic molecules, these same selection rules result if the vibration is of \(\sigma\) symmetry (i.e., has k = 0). If, on the other hand, the transition is of \(\pi\) symmetry (i.e., has k = ±1), so the transition dipole lies perpendicular to the molecule's axis, one obtains:
\[ \Delta M = \pm 1,0; \Delta L = \pm 1,0. \nonumber \]
These selection rules are derived by realizing that in addition to k = ±1, one has: (i) a linear-molecule rotational wavefunction that in the v = 0 vibrational level is described in terms of a rotation matrix \(\text{D}_{\text{L',M',0}} (\theta , \phi ,\chi )\) with no angular momentum along the molecular axis, K' = 0 ; (ii) a v = 1 molecule whose rotational wavefunction must be given by a rotation matrix \(\text{D}_{\text{L,M,1}} (\theta ,\phi , \chi )\) with one unit of angular momentum about the molecule's axis, K = 1. In the latter case, the angular momentum is produced by the degenerate \(\pi\) vibration itself. As a result, the selection rules above derive from the following product of 3-j symbols:
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 1 -1}} \right). \nonumber \]
Because \(\Delta L = 0\) transitions are allowed for \(\pi \text{ vibrations, one says that } \pi\) vibrations possess Q- branches in addition to their R- and P- branches (with \(\Delta L = 1 \text{ and } -1,\) respectively).
In the figure shown below, the v = 0 \(\rightarrow\) v = 1 (fundamental) vibrational absorption spectrum of HCl is shown. Here the peaks at lower energy (to the right of the figure) belong to P-branch transitions and occur at energies given approximately by:
\[ E = \hbar \omega_{\text{stretch}} + \left( \dfrac{h^2}{8\pi^2I} \right)((L - 1)L - L(L + 1)) = \hbar \omega_{\text{stretch}} -2\left( \dfrac{h^2}{8\pi^2 I} \right)L. \nonumber \]
The R-branch transitions occur at higher energies given approximately by:
\[ E = \hbar \omega_{\text{stretch}} + \left( \dfrac{h^2}{8\pi^2I} \right)((L+1)(L+2) - L(L + 1)) = \hbar \omega_{\text{stretch}} + 2\left( \dfrac{h^2}{8\pi^2I} \right)(L + 1). \nonumber \]
The absorption that is "missing" from the figure below lying slightly below 2900 cm-\(^{-1}\) is the Q-branch transition for which L = L'; it is absent because the selection rules forbid it.
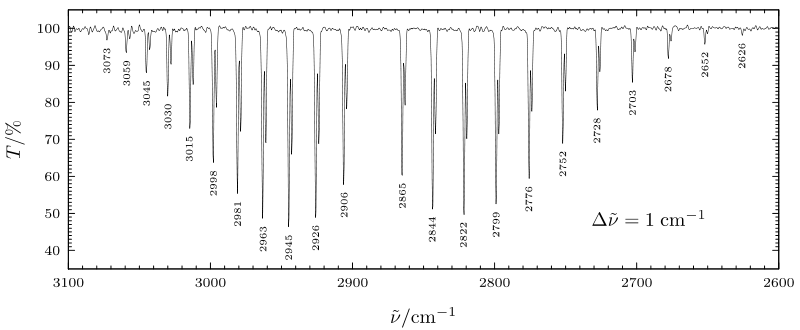
It should be noted that the spacings between the experimentally observed peaks in HCl are not constant as would be expected based on the above P- and R- branch formulas. This is because the moment of inertia appropriate for the v = 1 vibrational level is different than that of the v = 0 level. These effects of vibration-rotation coupling can be modeled by allowing the v = 0 and v = 1 levels to have rotational energies written as
\[ E = \hbar \omega_{\text{stretch}} \left( v + \dfrac{1}{2} \right) + \left( \dfrac{h^2}{8\pi^2I_v} \right) (L(L + 1)) \nonumber \]
where v and L are the vibrational and rotational quantum numbers. The P- and R- branch transition energies that pertain to these energy levels can then be written as:
\[ E_P = \hbar \omega_{\text{stretch}} - \left[ \left( \dfrac{h^2}{8\pi^2I_1} \right) + \left( \dfrac{h^2}{8\pi^2I_0}\right) \right] L + \left[ \left( \dfrac{h^2}{8\pi^2I_1} \right) - \left( \dfrac{h^2}{8\pi^2I_0} \right) \right] L^2 \nonumber \]
\[ E_R = \hbar\omega_{\text{stretch}} + 2\left( \dfrac{h^2}{8\pi^2I_1} \right) + 3\left[ \left( \dfrac{h^2}{8\pi^2I_1}\right) - \left( \dfrac{h^2}{8\pi^2I_0} \right) \right]L + \left[ \left( \dfrac{h^2}{8\pi^2I_1}\right) - \left( \dfrac{h^2}{8\pi^2I_0}\right) \right]L^2. \nonumber \]
Clearly, these formulas reduce to those shown earlier in the I1 = I0 limit.
If the vibrationally averaged bond length is longer in the v = 1 state than in the v = 0 state, which is to be expected, \(I_1\) will be larger than \(I_0\), and therefore \( \left[ \left( \dfrac{h^2}{8\pi^2I_1} \right) - \left( \dfrac{h^2}{8\pi^2I_0} \right) \right] \) will be negative. In this case, the spacing between neighboring P-branch lines will increase as shown above for HCl. In contrast, the fact that \( \left[ \left( \dfrac{h^2}{8\pi^2I_1} \right) - \left( \dfrac{h^2}{8\pi^2I_0} \right) \right] \) is negative causes the spacing between neighboring R- branch lines to decrease, again as shown for HCl.


