12.1: Concepts of Configuration and State Energies
- Page ID
- 63348
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Plots of CSF Energies Give Configuration Correlation Diagrams
The energy of a particular electronic state of an atom or molecule has been expressed in terms of Hamiltonian matrix elements, using the Slater-Condon rules, over the various spin-and spatially adapted determinants or CSFs which enter into the state wavefunction.
\[ E = \sum\limits_{I,J} \langle \Phi_I | H | \Phi_J \rangle C_IC_J. \nonumber \]
The diagonal matrix elements of H in the CSF basis multiplied by the appropriate CI amplitudes \(\langle \Phi_I | H | \Phi_I \rangle C_I C_I\) represent the energy of the \(I^{th}\) CSF weighted by the strength ( \(C_I^2\) ) of that CSF in the wavefunction. The off-diagonal elements represent the effects of mixing among the CSFs; mixing is strongest whenever two or more CSFs have nearly the same energy ( i.e., \(< \Phi_I | H | \Phi_I > \neq < \Phi_J | H | \Phi_J >\) ) and there is strong coupling ( i.e., \(< \Phi_I | H | \Phi_J >\) is large ). Whenever the CSFs are widely separated in energy, each wavefunction is dominated by a single CSF.
CSFs Interact and Couple to Produce States and State Correlation Diagrams
Just as orbital energies connected according to their symmetries and plotted as functions of geometry constitute an orbital correlation diagram, plots of the diagonal CSF energies, connected according to symmetry, constitute a configuration correlation diagram (CCD). If, near regions where energies of CSFs of the same symmetry cross (according to the direct product rule of group theory discussed in Appendix E, only CSFs of the same symmetry mix because only they have non-vanishing \(< \Phi_I | H | \Phi_J >\) matrix elements), CI mixing is allowed to couple the CSFs to give rise to "avoided crossings", then the CCD is converted into a so-called state correlation diagram ( SCD ).
CSFs that Differ by Two Spin-Orbitals Interact Less Strongly than CSFs that Differ by One Spin-Orbital
The strengths of the couplings between pairs of CSFs whose energies cross are evaluated through the Slater-Condon rules. CSFs that differ by more than two spin-orbital occupancies do not couple; the Slater-Condon rules give vanishing Hamiltonian matrix elements for such pairs. Pairs that differ by two spin-orbitals \((e.g. |.. \phi_a... \phi_b...| vs |.. \phi_{a'}... \phi_{b'}...| )\) have interaction strengths determined by the two-electron integrals < ab | a'b' > - < ab | b'a'>. Pairs that differ by a single spin-orbital \((e.g. |.. \phi_a... ...| vs |.. \phi_{a'}... ...| )\) are coupled by the one- and two- electron parts of \(H: < a | f | b> + \sum\limits_j [< aj | bj> - < aj | jb > ].\) Usually, couplings among CSFs that differ by two spin-orbitals are much weaker than those among CSFs that differ by one spin-orbital. In the latter case, the full strength of H is brought to bear, whereas in the former, only the electron-electron coulomb potential is operative.
State Correlation Diagrams
In the SCD, the energies are connected by symmetry but the configurational nature as reflected in the \(C_I\) coefficients changes as one passes through geometries where crossings in the CCD occur. The SCD is the ultimate product of an orbital and configuration symmetry and energy analysis and gives one the most useful information about whether reactions will or will not encounter barriers on the ground and excited state surfaces.
As an example of the application of CCD's and SCD's, consider the disrotatory closing of 1,3-butadiene to produce cyclobutene. The OCD given earlier for this proposed reaction path is reproduced below.
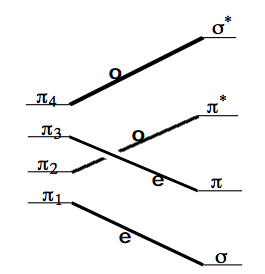
Recall that the symmetry labels e and o refer to the symmetries of the orbitals under reflection through the one \(C_v\) plane that is preserved throughout the proposed disrotatory closing. Low-energy configurations (assuming one is interested in the thermal or low-lying photochemically excited-state reactivity of this system) for the reactant molecule and their overall space and spin symmetry are as follows:
- \( \pi_1^2\pi_2^2 = 1e^21o^2, ^1Even \)
- \( \pi_1^2\pi_2^1\pi_3^1 = 1e^21o^12e^1, ^3\text{Odd and }^1\text{Odd.} \)
For the product molecule, on the other hand, the low-lying states are - \( \sigma^2\pi^2 = 1e^22e^2, ^1\text{Even} \)
- \( \sigma^2\pi^1\pi^{\text{*}1} = 1e^22e^1o^1, ^3Odd, ^1Odd. \)
Notice that although the lowest energy configuration at the reactant geometry \(\pi_1^2\pi_2^2 = 1e^21o^2\) and the lowest energy configuration at the product geometry \(\sigma^2\pi^2 = 1e^22e^2\) are both of 1Even symmetry, they are not the same configurations; they involve occupancy of different symmetry orbitals.
In constructing the CCD, one must trace the energies of all four of the above CSFs (actually there are more because the singlet and triplet excited CSFs must be treated independently) along the proposed reaction path. In doing so, one must realize that the \(1e^21o^2\) CSF has low energy on the reactant side of the CCD because it corresponds to \(\pi_1^2p_2^2\) orbital occupancy, but on the product side, it corresponds to \(\sigma^2\pi^{\text{*2}}\) orbital occupancy and is thus of very high energy. Likewise, the \(1e^22e^2\) CSF has low energy on the product side where it is \(\sigma^2\pi^2\) but high energy on the reactant side where it corresponds to \(\pi_1^2\pi_3^2.\) The low-lying singly excited CSFs are \(1e^22e^11o^1\) at both reactant and product geometries; in the former case, they correspond to \(\pi_1^2\pi_2^1\pi_3^1\) occupancy and at the latter to \(\sigma^2\pi^1\pi^{*1}\) occupancy. Plotting the energies of these CSFs along the disrotatory reaction path results in the CCD shown below.
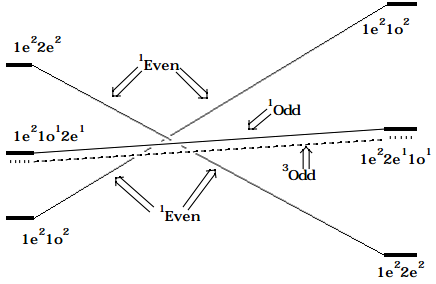
Figure 12.1.2: Insert caption here!
If the two \(^1\)Even CSFs which cross are allowed to interact (the Slater-Condon rules give their interaction strength in terms of the exchange integral \(< |1e^21o^2 | H |1e^22e^2 | > = < 1o1o | 2e2e > = K_{1o,2e}\) ) to produce states which are combinations of the two 1Even CSFs, the following SCD results:
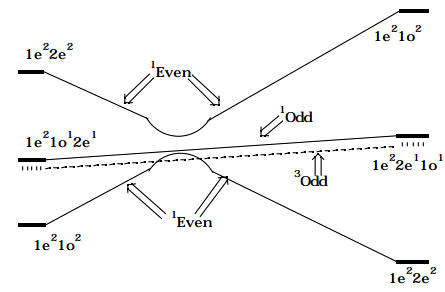
Figure 12.1.3: Insert caption here!
This SCD predicts that the thermal (i.e., on the ground electronic surface) disrotatory rearrangement of 1,3-butadiene to produce cyclobutene will experience a symmety-imposed barrier which arises because of the avoided crossing of the two 1Even configurations; this avoidance occurs because the orbital occupancy pattern (i.e., the configuration) which is best for the ground state of the reactant is not identical to that of the product molecule. The SCD also predicts that there should be no symmetry-imposed barrier for the singlet or triplet excited-state rearrangement, although the reaction leading from excited 1,3-butadiene to excited cyclobutene may be endothermic on the grounds of bond strengths alone.
It is also possible to infer from the SCD that excitation of the lowest singlet \(\pi\pi^{\text{*}}\) state of 1,3-butadiene would involve a low quantum yield for producing cyclobutene and would, in fact, produce ground-state butadiene. As the reaction proceeds along the singlet \(\pi\pi^{\text{*}}\) surface this \(^1\)Odd state intersects the ground \(^1\)1Even surface on the reactant side of the diagram; internal conversion ( i.e., quenching from the \(^1\)Odd to the \(^1\)Even surfaces induced by using a vibration of odd symmetry to "digest" the excess energy (much like vibronic borrowing in spectroscopy) can lead to production of ground-state reactant molecules. Some fraction of such events will lead to the system remaining on the \(^1\)Odd surface until, further along the reaction path, the \(^1\)Odd surface again intersects the \(^1\)Even surface on the product side at which time quenching to produce ground-state products can occur. Although, in principle, it is possible for some fraction of the events to follow the \(^1\)Odd surface beyond this second intersection and to thus lead to \(^1\)Odd product molecules that might fluoresce, quenching is known to be rapid in most polyatomic molecules; as a result, reactions which are chemiluminescent are rare. An appropriate introduction to the use of OCD's, CCD's, and SCD's as well as the radiationless processes that can occur in thermal and photochemical reactions is given in the text Energetic Principles of Chemical Reactions , J. Simons, Jones and Bartlett, Boston (1983).


