20.7: Thermodynamics Provides Insight into the Conversion of Heat into Work
- Page ID
- 13721
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Heat and work are both forms of transferring energy, and under the right circumstance, one form may be transformed into the other. However, the second law of thermodynamics puts a limitation on this. To go from work to heat is called dissipation and there is no limitation on this at all. In fact it was through dissipation (by friction) that we discovered that heat and work were both forms of energy. There is, however, a limitation on converting heat to work.
The Carnot Cycle
Let's consider a circular, reversible path of an ideal gas on a PV diagram:
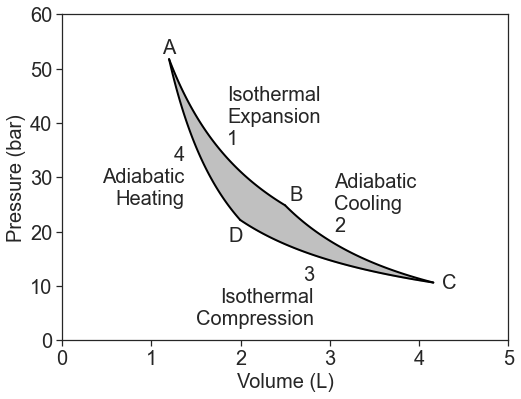
This cycle forms the 4-stage Carnot cycle heat engine. A heat engine converts heat energy into work. The cycle consists of:
- Isothermal expansion at the hot temperature, \(T_h\): \[\Delta U_1=w_1+q_h=0 \nonumber \]
- Adiabatic cooling from \(T_h\) to \(T_c\): \[\Delta U_2=w_2 \nonumber \]
- Isothermal compression at the cold temperature, \(T_c\): \[\Delta U_3=w_3+q_c=0 \nonumber \]
- Adiabatic heating from \(T_c\) to \(T_h\): \[\Delta U_4=w_4 \nonumber \]
The total four-step process produces work because \(w_{hot} > w_{cold}\). The work is the integral under the upper isotherm minus the one under the lower curve, i.e.the surface area in between.
Sadi Carnot was a French engineer at the beginning of the 19th century. He considered a cyclic process involving a cylinder filled with gas. This cycle the Carnot cycle contributed greatly to the development of thermodynamics and the improvement of the steam engine. Carnot demonstrated that the cold temperature on the right is as important as the heat source on the left in defining the possible efficiency of a heat engine
Efficiency
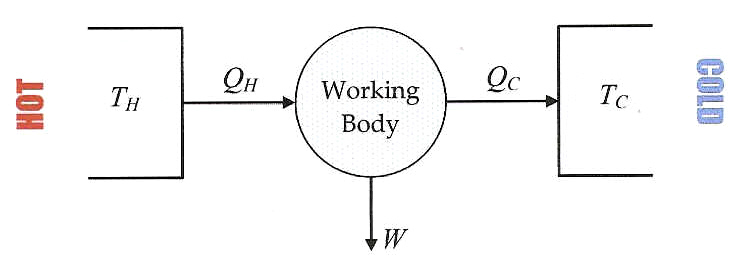
Of course we spend good money on the fuel to start the cycle by heating things up. So how much work do we get for the heat we put in? In other words, we want to know how efficient our heat engine is. The efficiency, \(\eta\) of a heat engine is:
\[\eta=\frac{|w_\text{cycle}|}{q_h}=\frac{q_h+q_c}{q_h}=1+\frac{q_c}{q_h} \nonumber \]
To get the work of the cycle, we can make use of internal energy as a state function. As the path is circular the circular integrals for \(U\) is zero:
\[\begin{align*} \oint{dU} &= \Delta U_{\text{cycle}} \\[4pt] &=\sum{\Delta U_i} \\[4pt] &=w_1+q_h+w_2+w_3+q_c+w_4 \\[4pt] &=0 \end{align*} \]
Rearranging:
\[\begin{align*} q_h + q_c &=-w_1-w_2-w_3-w_4 \\[4pt] &=-w_\text{cycle} \end{align*} \]
An ideal engine would take \(q_h\rightarrow q_c\) with 100% efficiency. The work of the cycle will be equivalent to the heat transfer. For ideal gases:
- \(w_1=-RT_h\ln{\left(\frac{V_B}{V_A}\right)}=-q_h\)
- \(dU=\delta w=\bar{C}_VdT\rightarrow w_2={\bar{C}}_V\left(T_c-T_h\right)\)
- \(w_3=-RT_c\ln{\left(\frac{V_D}{V_C}\right)}=-q_c\)
- \(w_4={\bar{C}}_V\left(T_h-T_c\right)\)
Finding an expression for \(w_\text{cycle}\):
\[\begin{split} w_\text{cycle} &= -RT_h\ln{\left(\frac{V_B}{V_A}\right)}+{\bar{C}}_V\left(T_c-T_h\right)-RT_c\ln{\left(\frac{V_D}{V_C}\right)}+{\bar{C}}_V\left(T_h-T_c\right) \\ &= -RT_h\ln{\left(\frac{V_B}{V_A}\right)}-RT_c\ln{\left(\frac{V_D}{V_C}\right)}= -R(T_h-T_c)\ln{\left(\frac{V_B}{V_A}\right)} \end{split} \nonumber \]
We have an expression for work, so we can evaluate the efficiency, \(\eta\). The efficiency of the Carnot engine is:
\[\eta=\frac{|w_\text{cycle}|}{q_h}=\frac{R\left(T_h-T_c\right)\ln{\left(\frac{V_B}{V_A}\right)}}{RT_h\ln{\left(\frac{V_B}{V_A}\right)}}=\frac{T_h-T_c}{T_h}=1-\frac{T_c}{T_h} \nonumber \]
Paths (2) and (4) are adiabats, so we can also use entropy, \(S\), to get the same solution:
\[\oint{dS}= \frac{q_h}{T_h}+\frac{q_c}{T_c}=0 \nonumber \]
Therefore:
\[ \dfrac{q_c}{q_h} = -\dfrac{T_c}{T_h} \nonumber \]
And we get that:
\[η= 1+ \dfrac{q_c}{q_h} = 1-\dfrac{T_c}{T_h} \label{eff} \]
As you see we can only get full efficiency if \(T_{cold}\) is 0 K, which is never (i.e., we always waste energy). Another implication is that if \(T_c = T_h\) then no work can be obtained, no matter how much energy is available in the from of heat. Or in other words, if one dissipates work into heat isothermally, none of it can be retrieved. Equation \(\ref{eff}\) is not very forgiving at all. Just imaging that you have a heat source of say 400 K (a superheated pool of water, e.g. a geyser) and you are dumping in the river at room temperature 300 K. The best efficiency you'll ever get is:
\[η= 1-\dfrac{300}{400}= 24\% \nonumber \]
Sadly, you'd be dumping three quarters of your energy as heat in the river (and that is best case scenario as there are always more losses, e.g. due to friction). The arrow saying \(Q_C\) in Figure 20.7.3 should then be three times as fat as the one that says \(w\).
Heat pumps
So getting our work from heat is hard and always less than 100% successful. The other way around should be easy. After all, we can dissipate work into heat freely even under isothermal conditions!
What happens if we let the heat engine run backwards? Consider reversing all the flows in the above diagram. Obviously we must put in work to make the cycle run in reverse. The heat will now flow from cold to hot, say from your cold garden into your nice and warm apartment. The amount of heat you get in your humble abode will be the sum of all the work (say 100 Joules) you dissipate plus the heat you pumped out of the garden (say 300 Joules). Thus if you are willing to pay for the energy you dissipate (100 Joules), you may well end up with a total of 400 Joules of heat in your apartment! Obviously if it is heat you after this is a better deal than just dissipating the work in your apartment (by burning some oil). Then you'd only get 100 J for your precious buck.
Dissipating it as electrical heating is even worse because you would
- first burn (a lot more!) oil to generate heat
- use this heat to produce electrical work at great expense because a lot of the heats gets dumped at the low temperature side (the river or so)
- dissipate the work again in your apartment (without using it to pump any heat out of the garden)
Refrigerators are also heat pumps. They heat the kitchen by pumping heat from its innards to the kitchen. If I keep the door open, however, all it does is dissipate precious electrical work, because the pumped heat will flow back into its innards and spoil the milk.
Stirling Engine
Let's consider another type of heat engine, the Stirling engine. The Stirling engine uses a circular reversible path in an ideal PV diagram:

The path consists of four steps:
- Isothermal expansion at the hot temperature \(T_h\): \[q_1=q_h =-w \nonumber \] and we get work out (i.e., negative work): \[w_h =-RT_h \ln \left( \dfrac{V_B}{V_A} \right) \nonumber \]
- Isochoric heating from \(T_c\) to \(T_h\) (with constant \(C_V\)): \[q_2= \dfrac{C_V}{ΔT} \label{q2} \]
- Isothermal compression at the cold temperature \(T_c\): \[q_3=q_c =-w \nonumber \] and we must put work in (i.e., positive work): \[w_c =-RT_c \ln \left( \dfrac{V_D}{V_C}\right)=RT_c \ln \left( \dfrac{V_B}{V_A} \right) \nonumber \]
- Isochoric cooling from \(T_h\) to \(T_c\) (with constant \(C_V\)): \[q_4= -\dfrac{C_V}{ΔT} \label{q4} \]
Notice that this gray area vanishes if \(T_{h}= T_{c}\). Obviously how cold the cold side is of great importance! The amount of work is also equal to the difference in the heat picked up at high temperature \(q_h\) and dumped at low temperature \(q_{c}\). The isochoric heats cancel. The problem is that \(q_{c}\) is only zero if the cold temperature is 0 K. That means that we can never get all the heat we pick up at high temperatures to come out as work.

