5.1: A Harmonic Oscillator Obeys Hooke's Law
- Page ID
- 13413
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The motion of two atoms in a diatomic molecule can be separated into translational, vibrational, and rotational motions. Both rotation and vibrational motions are internal motions that do not change the center of mass for the molecule (Figure 5.1.1 ), which is described by translational motion. Quantum translational motions can be modeled with the particle in a box model discussed previously and rotation and vibration can be modeled via the rigid rotor and harmonic oscillator models, respectively.
Before delving into the quantum mechanical harmonic oscillator, we will introduce the classical harmonic oscillator (i.e., involving classical mechanics) to build an intuition that we will extend to the quantum world. A classical description of the vibration of a diatomic molecule is needed because the quantum mechanical description begins with replacing the classical energy with the Hamiltonian operator in the Schrödinger equation. It also is interesting to compare and contrast the classical description with the quantum mechanical picture.
The Classical Harmonic Oscillator
Simple harmonic oscillators about a potential energy minimum can be thought of as a ball rolling frictionlessly in a curved dish or a pendulum swinging frictionlessly back and forth (Figure 5.1.2 ). The restoring forces are precisely the same in either horizontal direction.
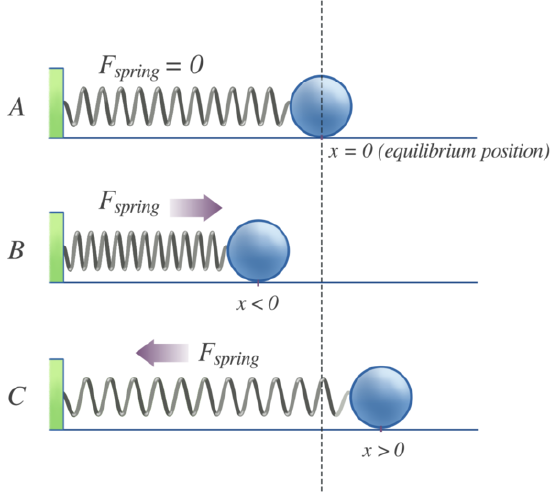
If we consider the bond to behave like a mass on a spring (Figure 5.1.2 ), then this restoring force (\(F\)) is proportional to the displacement (\(x\)) from the equilibrium length (\(x_o\)) - this is Hooke's Law:
\[ F = - kx \label {5.1.2} \]
where \(k\) is the force constant. Hooke's Law says that the force is proportional to, but in opposite direction to, the displacement (\(x\)). The force constant reflects the stiffness of the spring. The idea incorporated into the application of Hooke's Law to a diatomic molecule is that when the atoms move away from their equilibrium positions, a restoring force is produced that increases proportionally with the displacement from equilibrium. The potential energy for such a system increases quadratically with the displacement.
\[ V (x) = \dfrac {1}{2} k x^2 \label {5.1.3} \]
Hooke's Law or the harmonic (i.e. quadratic) potential given by Equation \(\ref{5.1.3}\) is an excellent approximation for the vibrational oscillations of molecules. The magnitude of the force constant \(k\) depends upon the nature of the chemical bond in molecular systems just as it depends on the nature of the spring in mechanical systems. The larger the force constant, the stiffer the spring or the stiffer the bond. Since it is the electron distribution between the two positively charged nuclei that holds them together, a double bond with more electrons has a larger force constant than a single bond, and the nuclei are held together more tightly.
A stiff bond with a large force constant is not necessarily a strong bond with a large dissociation energy. A harmonic oscillator has no dissociation energy since it CANNOT be broken - there is always a restoring force to keep the molecule together. This is one of many deficiencies in using the harmonic oscillator model to describe molecular vibrations.
You may have questioned the applicability of the harmonic oscillator model involving one moving mass bound to a fix wall via a spring like in Figure 5.1.2 for the vibration of a diatomic molecule with two moving masses like in Figure 5.1.1 . It turned out the two are mathematically the same with internal vibration motion described by a single reduced particle with a reduced mass \(μ\).
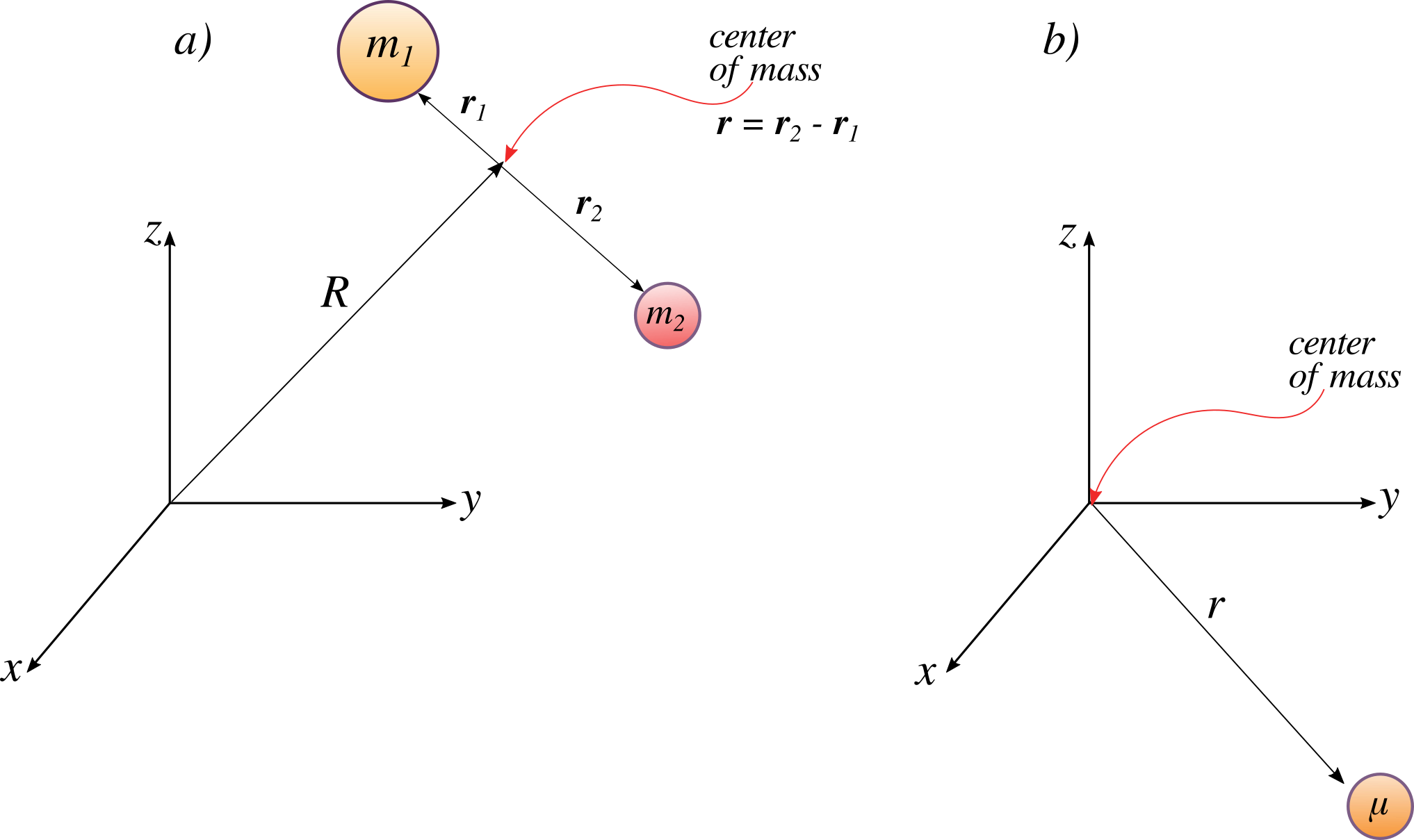
For a diatomic molecule, Figure 5.1.3 , the vector \(\vec{r}\) corresponds to the internuclear axis. The magnitude or length of \(r\) is the bond length, and the orientation of \(r\) in space gives the orientation of the internuclear axis in space. Changes in the orientation correspond to rotation of the molecule, and changes in the length correspond to vibration. The change in the bond length from the equilibrium bond length is the vibrational coordinate for a diatomic molecule.
- Show that minus the first derivative of the harmonic potential energy function in Equation \(\ref{5.1.3}\) with respect to \(x\) is the Hooke's Law force in Equation \ref{5.1.2}.
- Show that the second derivative is the force constant, \(k\).
- At what value of \(x\) is the potential energy a minimum; at what value of \(x\) is the force zero?
- Sketch graphs to compare the potential energy and the force for a system with a large force constant to one with a small force constant.
Solution a
Hooke's Law for a spring entails that the force applied on a spring \(F\) is equal to the force constant, \(-k\) times the distance compressed or stretched, \(x\) (Equation \ref{5.1.2}). The derivative of \(V(x) = 0.5 k x^2\) is
\[V'(x) = (2)\left(\dfrac{1}{2}\right)kx = kx. \nonumber \]
The negative of this is \(-V'(x) = -kx\) which is exactly equal to Hooke's Law.
Solution b
The second derivative
\[V"(x) = \dfrac{d}{dx} kx = k \nonumber \]
Thus, the second derivative of this equation for potential energy is equal to the force constant, \(k\).
Solution c
To find the minimum potential energy, it is easiest to set the first derivative equal to zero and solve for x. When \(V'(x) = kx = 0\) then x must be equal to zero. Thus, the minimum potential energy is when x=0. Plugging this into Hooke's Law, \(F(0) = -k(0) = 0\) so this is also the value for x when the force is zero.
Solution d
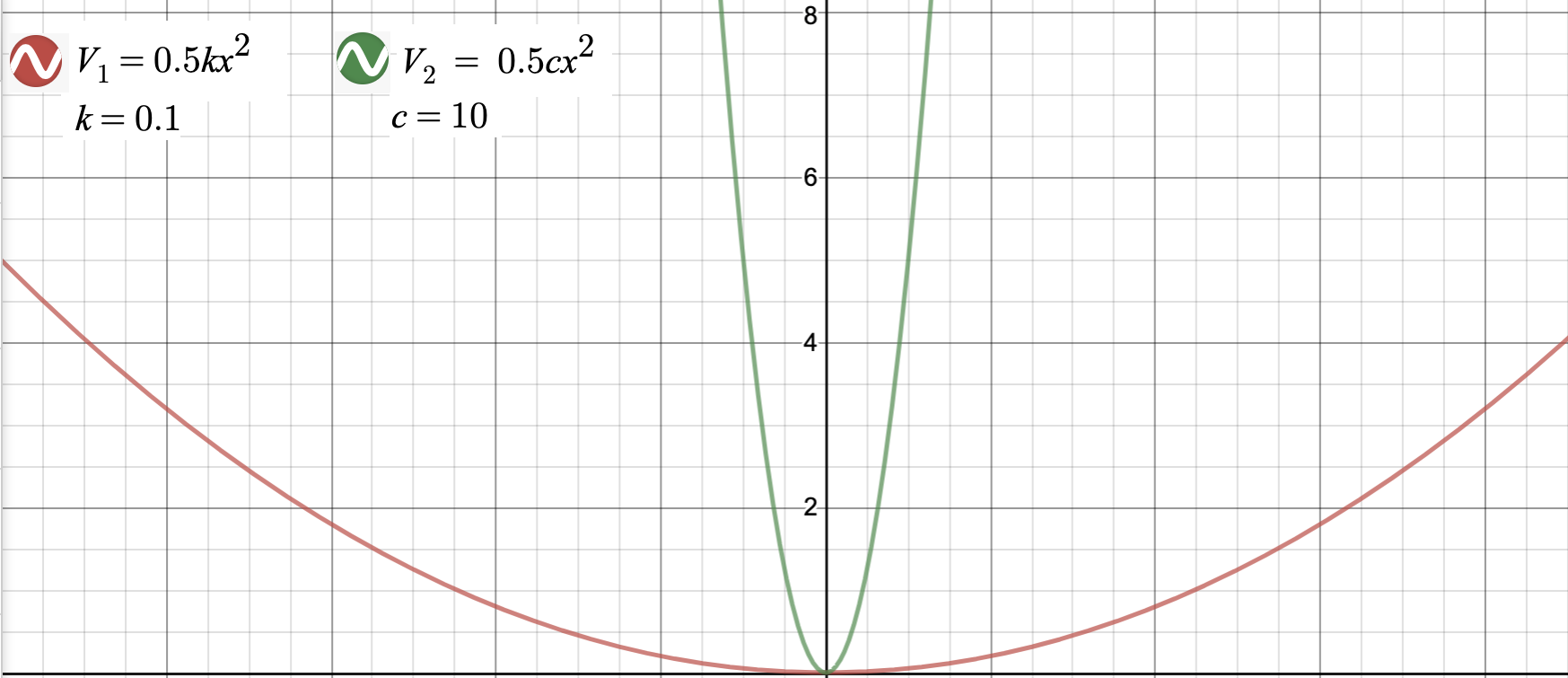
The force constant has a drastic effect on both the potential energy and the force. A system with a large force constant requires minimal change in \(x\) to have a drastic change in potential energy or force, whereas a system with a small force constant is the exact opposite phenomenon.
Solving the Harmonic Oscillator Model
The classical equation of motion for a one-dimensional simple harmonic oscillator with a particle of mass \(m\) attached to a spring having spring constant \(k\) is
\[ m \dfrac{d^2x(t)}{dt^2} = -kx(t) \label{5.1.4a} \]
which can be rewritten in the standardform:
\[ \dfrac{d^2x(t)}{dt^2} + \dfrac{k}{m}x(t) = 0 \label{5.1.4b} \]
Equation \(\ref{5.1.4a}\) is a linear second-order differential equation that can be solved by the standard method of factoring and integrating. The resulting solution to Equation \(\ref{5.1.4a}\) is
\[ x(t) = x_o \sin (\omega t + \phi) \label{5.1.5} \]
with
\[\omega = \sqrt{\dfrac{k}{m}} \label{5.1.6} \]
and the momentum \(\) has time dependence
\[\begin{align*} p &= mv \\[4pt] &=mx_o \omega \cos (\omega t + \phi) \label{5.1.7} \end{align*} \]
Figure 5.1.4 show the displacement of the bond from its equilibrium length as a function of time. Such motion is called harmonic.
Substitute the following functions into Equation \(\ref{5.1.4b}\) to demonstrate that they are both possible solutions to the classical equation of motion.
- \(x(t) = x_0 e^{i \omega t} \)
- \(x(t) = x_0 e^{-i \omega t}\)
where
\[ \omega = \sqrt {\dfrac {k}{m}} \nonumber \]
Note that the Greek symbol \(\omega\) for frequency represents the angular frequency \(2π\nu\).
Solution a
This requires simply placing the given function \(x(t) = x_0 e^{i \omega t} \) into Equation \(\ref{5.1.4b}\).
\[ \begin{align*} \frac{d^2 x(t) }{dt^2} + \frac{k}{m} x(t) &= 0 \\[4pt] \frac{d^2 }{dt^2} \left( x_o e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0\\[4pt] x_o \frac{d^2 }{dt^2} \left( e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 \left( e^{i \omega t} \right)+ \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 e^{i \omega t} + \frac{k}{m}x_o e^{i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 + \frac{k}{m}x_o &= 0 \\[4pt] -x_o \frac{k}{m}+ \frac{k}{m}x_o = 0 \; \textrm{ with } \; \omega &= \sqrt{\frac{k}{m}} \end{align*} \nonumber \]
Solution b
This requires simply placing the given function \(x(t) = x_0 e^{-i \omega t}\) into Equation \(\ref{5.1.4b}\).
\[ \begin{align*} \frac{d^2 x(t) }{dt^2} + \frac{k}{m} x(t) &= 0 \\[4pt] \frac{d^2 }{dt^2} \left( x_o e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t}& = 0 \\[4pt] x_o \frac{d^2 }{dt^2} \left( e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 \left( e^{-i \omega t} \right)+ \frac{k}{m}x_o e^{-i \omega t} &= 0 \\[4pt] x_o i^2 \omega^2 e^{-i \omega t} + \frac{k}{m}x_o e^{-i \omega t}& = 0\\[4pt] x_o i^2 \omega^2 + \frac{k}{m}x_o &= 0 \\[4pt] -x_o \frac{k}{m}+ \frac{k}{m}x_o = 0 \; \textrm{ with } \; \omega &= \sqrt{\frac{k}{m}} \end{align*} \nonumber \]
Show that sine and cosine functions also are solutions to Equation \(\ref{5.1.4b}\).
- Answer
-
Using Equation \(\ref{5.1.4b}\)
\[\frac{d^2x(t)}{dt^2} +\frac{k}{m}x(t)=0 \nonumber \]
with \(\omega =\sqrt{\frac{k}{m}}\).
For
\[\begin{align*} x(t)=x_{o} \sin(\omega t+\phi) \end{align*} \nonumber \]
Take the second derivative of \(x(t)\)
\[\begin{align*} \frac{d^2x(t)}{dt} &=-\omega^2x_{o}\sin(\omega t+\phi) \\[4pt] &= \omega^2 x_{o}\sin(\omega t+\phi) \\[4pt] &=-\frac{k}{m}x_{o} \sin \left(\sqrt{\frac{k}{m}}t+\phi \right) \end{align*} \nonumber \]
Plug in \(x(t)\) and the second derivative of \(x(t)\) into Equation \(\ref{5.1.4b}\)
\[\begin{align*} -\frac{k}{m}x_{o}\sin \left(\sqrt{ \frac{k}{m}} t + \phi \right) + \frac{k}{m} x_{o} \sin \left(\sqrt{\frac{k}{m}} t + \phi \right) =0 \end{align*} \nonumber \]
Hence, the sine equation is a solution to Equation \(\ref{5.1.4b}\)
We do the same for the cosine function
\[x(t)=x_{o}\cos(\omega t + \phi) \nonumber \]
Take the second derivative of \(x(t)\)
\[ \begin{align*} \frac{d^2x(t)}{dt} &=-\omega^2x_{o}\cos(\omega t + \phi) \\[4pt] &= -\omega^2x_{o}\cos( \omega t +\phi) \\[4pt] &=-\frac{k}{m} x_{o} \cos\left( \sqrt{\frac{k}{m}} t + \phi \right ) \end{align*} \nonumber \]
Plug in \(x(t)\) and the second derivative of \(x(t)\) into Equation \(\ref{5.1.4b}\)
\[\begin{align*} -\frac{k}{m}x_{o} \cos\left( \sqrt{\frac{k}{m}} t + \phi \right) + \frac{k}{m}x_{o} \cos\left( \sqrt{\frac{k}{m}}t + \phi \right)=0 \end{align*} \nonumber \]
The cosine equation is also a solution to Equation \(\ref{5.1.4b}\).
Identify what happens to the frequency of the motion as the force constant increases in one case and as the mass increases in another case. If the force constant is increased 9-fold and the mass is increased by 4-fold, by what factor does the frequency change?
- Answer
-
This is a simple application of Equation \ref{5.1.6}. As the force constant increases, the frequency of the motion increases, while as the mass increases, the frequency of the motion decreases. If the force constant increased 9-fold and the mass increased 4-fold,
\[ω=\sqrt{\dfrac{9k}{4m}}= \dfrac{3}{2} \left(\dfrac{k}{m}\right) \nonumber \]
The entire frequency of motion would increase by a factor of 3/2.
Harmonic Oscillator Energies
The energy of the vibration is the sum of the kinetic energy and the potential energy. The momentum associated with the harmonic oscillator is
\[p = m \dfrac {dx}{dt} \label {5.1.8} \]
so combining Equations \ref{5.1.8} and \ref{5.1.3}, the total energy can be written as
\[ \begin{align} E &= T + V \\[4pt] &= \dfrac {p^2}{2 m} + \dfrac {k}{2} x^2 \label {5.1.9} \end{align} \]
The total energy of the harmonic oscillator is equal to the maximum potential energy stored in the spring when \(x = \pm A\), called the turning points (Figure 5.1.5 ). The total energy (Equation \(\ref{5.1.9}\)) is continuously being shifted between potential energy stored in the spring and kinetic energy of the mass.
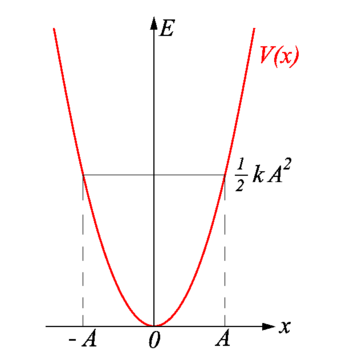
The motion of a classical oscillator is confined to the region where its kinetic energy is nonnegative, which is what the energy relation Equation \ref{5.1.9} says. Physically, it means that a classical oscillator can never be found beyond its turning points, and its energy depends only on how far the turning points are from its equilibrium position. The energy of a classical oscillator changes in a continuous way. The lowest energy that a classical oscillator may have is zero, which corresponds to a situation where an object is at rest at its equilibrium position. The zero-energy state of a classical oscillator simply means no oscillations and no motion at all (a classical particle sitting at the bottom of the potential well in Figure 5.1.5 ). When an object oscillates, no matter how big or small its energy may be, it spends the longest time near the turning points, because this is where it slows down and reverses its direction of motion. Therefore, the probability of finding a classical oscillator between the turning points is highest near the turning points and lowest at the equilibrium position. (Note that this is not a statement of preference of the object to go to lower energy. It is a statement about how quickly the object moves through various regions.)
- What happens to the frequency of the oscillation as the vibration is excited with more and more energy?
- What happens to the maximum amplitude of the vibration as it is excited with more and more energy?
Solution
a. Frequency
The energy of the harmonic oscillator can be written as
\[E_{v}=h v\left(v+\dfrac{1}{2}\right) \nonumber \]
and the frequency of oscillation is \(\omega=\sqrt{\frac{k}{m}}\). Notice that the frequency depends only on the stiffness (\(k\)) and reduced mass (\(\mu\)) of the oscillator and not on the energy. Hence, increasing the energy of the vibrations does not affects its frequency.
b. Amplitude
The kinetic and potential terms for energy of the harmonic oscillator can be written as
\[\begin{align*} E &=K+V \\[4pt] &=\frac{1}{2} m \omega^{2} A^{2} \sin ^{2} \omega t+\frac{1}{2} k A^2 \cos^2 \omega t \end{align*} \nonumber \]
with \(\omega=\sqrt{\frac{k}{m}}\) so
\[\begin{align*} E &=\frac{1}{2} k A^{2}\left(\sin ^{2} \omega t+\cos^2 \omega t\right) \\[4pt] &= \frac{1}{2} k A^2 \end{align*} \nonumber \]
The maximum amplitude of the vibration will increase as the energy increases.
If a molecular vibration is excited by collision with another molecule and is given a total energy \(E_{hit}\) as a result, what is the maximum amplitude of the oscillation? Is there any constraint on the magnitude of energy that can be introduced?
- Answer
-
The equation that defines the energy of a molecular vibration can be approximated is:
\[E_{h i t}=T+V=\frac{p^{2}}{2 m}+\frac{k}{2} x \nonumber \]
The maximum amplitude of a harmonic oscillator is equal to x when the kinetic energy term of total energy equals zero
\[E_{hit}=\frac{k}{2}x \nonumber \]
Solving for x gives the maximum amplitude:
\[x=\sqrt{\frac{2}{k} E_{h i t}} \nonumber \]
The constraint for the energy that can be introduced cannot be greater than the energy required to break the bond between atoms.
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")

