2.7: Real Gases
- Page ID
- 84445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)While the ideal gas law is sufficient for the prediction of large numbers of properties and behaviors for gases, there are a number of times that deviations from ideality are extremely important.
The van der Waals Equation
Several equations of state have been suggested to account for the deviations from ideality. One simple, but useful, expression is that proposed by Johannes Diderik van der Waals (1837 – 1923) (Johannes Diderik van der Waals - Biographical, 2014)

van der Waals’ equation introduced corrections to the pressure and volume terms of the ideal gas law in order to account for intermolecular interactions and molecular size respectively.
\[ \left ( p + \dfrac{a}{V_m^2} \right) (V_m - b) = RT \label{vdw} \]
or
\[ p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2} \label{vdw2} \]
In this expression, \(a\) and \(b\) are variables of a given substance which can be measured and tabulated. In general, molecules with large intermolecular forces will have large values of \(a\), and large molecules will have large values of b. Some van der Waals constants are given in Table \(\PageIndex{1}\).
| Gas frequency of collisions | a (atm L2 mol-2) | b (L/mol) |
|---|---|---|
| He | 0.0341 | 0.0238 |
| N2 | 1.352 | 0.0387 |
| CO2 | 3.610 | 0.0429 |
| C2H4 | 4.552 | 0.0305 |
The van der Walls model is useful because it makes it so simple to interpret the parameters in terms of molecular size and intermolecular forces. But it does have limitations as well (as is the case of every scientific model!) Some other useful two-parameter and three-parameter (or more) equations of state include the Redlich-Kwong, Dieterici, and Clausius models (Table \(\PageIndex{2}\)). These have the advantage that they allow for temperature dependence on some of the parameters, which as will be seen later, is necessary to model certain behaviors of real gases.
| Model | Equation of State |
|---|---|
| Ideal | \(p = \dfrac{RT}{V_m}\) |
| van der Waals (van der Waals J. D., 1867) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{V_m^2}\) |
| Redlich-Kwong (Redlich & Kwong, 1949) | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{\sqrt{T} V_m (V_m +b)}\) |
| Dieterici (Dieterici, 1899) | \( p =\dfrac{RT}{V_m-b} \exp \left( \dfrac{-a}{V_mRT} \right)\) |
| Clausius | \( p =\dfrac{RT}{V_m-b} - \dfrac{a}{T (V_m + c)^2}\) |
| Virial Equations | \( p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m} \dots \right) \) |
The Virial Equation
A very handy expression that allows for deviations from ideal behavior is the Virial Equation of state. This is a simple power series expansion in which the higher-order terms contain all of the deviations from the ideal gas law.
\[ p =\dfrac{RT}{V_m} \left(1+ \dfrac{B(T)}{V_m} +\dfrac{C(T)}{V_m^2} \dots \right ) \label{viral} \]
In the limit that \(B(T)\) (the Second Virial Coefficient) and \(C(T)\) are zero, the equation becomes the ideal gas law. Also, the molar volume of gases are small, the contributions from the third, fourth, etc. terms decrease in magnitude, allowing one to truncate the series at a convenient point. The second virial coefficient can be predicted from a theoretical intermolecular potential function by
\[B(T) = N_a \int _{r=0}^{\infty} \left[ 1- \exp \left(\dfrac{U(r)}{k_BT} \right) \right] 2\pi r^2 \,dr \nonumber \]
The quality of an intermolecular potential can be determined (partially) by the potential’s ability to predict the value of the second virial coefficient, \(B(T)\).
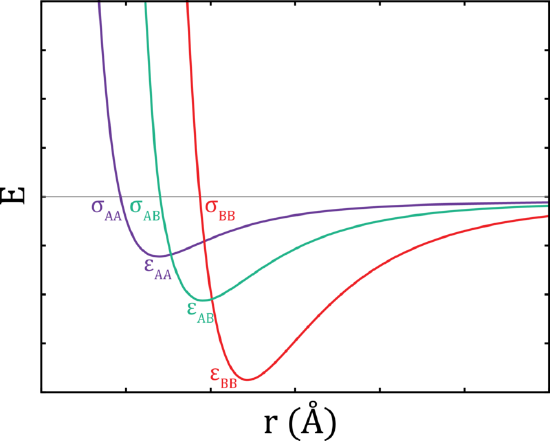
The Leonard-Jones Potential
An intermolecular potential function is used to describe the interactions between molecules. These interactions will have to include attractive forces, which will draw molecules together, and repulsive forces which will push them apart. If the molecules are hard spheres, lacking any attractive interactions, the potential function is fairly simple.
\[ U(r) ={\begin{cases} \infty &{\text{for }}r\leq \sigma\\0&{\text{for }}r>\sigma.\end{cases}} \nonumber \]
In this function, \(\sigma\) is determined by the size of the molecules. If two molecules come within a distance \(r\) of one another, they collide, bouncing off in a perfectly elastic collision. Real molecules, however, with have a range of intermolecular separations through which they will experience attractive forces (the so-called “soft wall” of the potential surface.) And then at very small separations, the repulsive forces will dominate, pushing the molecules apart (the so-called “hard wall” of the potential surface.)
A commonly used intermolecular potential, \(U(r)\), is the Leonard-Jones potential. This function has the form
\[ U(r) = 4 \epsilon \left[ \underbrace{\left(\dfrac{\sigma}{r}\right)^{12}}_{\text{repulsive term}} - \underbrace{\left(\dfrac{\sigma}{r}\right)^{6}}_{\text{attractive term}} \right] \nonumber \]
where \(\sigma\) governs the width of the potential well, and \(\epsilon\) governs the depth. The distance between molecules is given by \(r\). The repulsive interactions between molecules are contained in the first terms and the attractive interactions are found in the second term.
A commonly used method of creating a power series based on another equation is the Taylor Series Expansion. This is an expansion of a function about a useful reference point where each of the terms is generated by differentiating the original function.
For a function \(f(x)\), the Taylor series \(F(x)\) can be generated from the expression
\[F(x) = f(a) + \left.\dfrac{d}{dx} f(x) \right|_{x=a} (x-a) + \dfrac{1}{2!} \left. \dfrac{d^2}{dx^2} f(x) \right|_{x=a} (x-a)^2 + \dots \nonumber \]
This can be applied to any equation of state to derive an expression for the virial coefficients in terms of the parameters of the equation of state.
The van der Waals equation can be written in terms of molar volume (Equation \ref{vdw2}). When multiplying the right hand side by \(\frac{u}{u}\) (where \(u = 1/v\)) yields:
\[ p =\dfrac{RTu}{1-bu} - au^2 \nonumber \]
This expression can be "Talyor" expanded (to the first three terms) about \(u = 0\) (which corresponds to an infinite molar volume.) The coefficient terms that are needed for the expansion are
\[p(u=0)=0 \nonumber \]
\[ \dfrac{dp}{du} \big|_{u=0} = \left [ \dfrac{RT}{1-bu} + \dfrac{bRTu}{(1-bu)^2} - 2au \right]_{u=0} = RT \nonumber \]
\[ \dfrac{d^2p}{du^2} \big|_{u=0} = \dfrac{1}{2} \left [ \dfrac{bRT}{(1-bu)^2} + \dfrac{bRT}{(1-bu)^2} - \dfrac{2b^2RTu}{(1-bu)^3} - 2au \right]_{u=0} = RT -a \nonumber \]
\[ \dfrac{d^3p}{du^3} \big|_{u=0} = RTb^2 \nonumber \]
And the virial equation can then be expressed in terms of the van der Waals parameters as
\[ p = 0 +RT(u) + (bRT -a)(u)^2 + RTb^{2(u)^3} \nonumber \]
Substituting \(u = 1/V\) and simplifying gives the desired result:
\[ p= RT \left[ \dfrac{1}{V} + \dfrac{b-\frac{a}{RT}}{V^2} + \dfrac{b^2}{V^3} + \dots \right] \nonumber \]
And the second virial coefficient is given by
\[ B(T) = b-\dfrac{a}{RT} \nonumber \]
The Boyle Temperature
A useful way in which deviations from ideality can be expressed is by defining the compression factor (\(Z\)) given by
\[ Z = \dfrac{pV_m}{RT} \nonumber \]
where \(V_m\) is the molar volume. For an ideal gas, \(Z = 1\) under all combinations of \(P\), \(V_m\), and \(T\). However, real gases will show some deviation (although all gases approach ideal behavior at low p, high Vm, and high T.) The compression factor for nitrogen at several temperatures is shown below over a range of pressures.
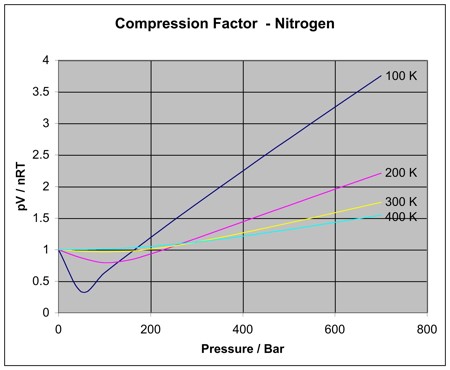
As can be seen, the gas behaves closer to ideally over a longer range of pressure at the higher temperatures. In general, there is one temperature, the Boyle temperature, at which a gas will approach ideal behavior as the pressure goes to zero asymptotically, and thus behave ideally over a broad range of lower pressures. The Boyle temperature is found by solving
\[ \lim_{p \rightarrow 0} \left( \dfrac{\partial Z}{\partial p} \right) = 0 \nonumber \]
or
\[ \lim_{1/V_m \rightarrow 0} \left( \dfrac{\partial Z}{\partial \left(\frac{1}{V_m} \right)} \right) = 0 \nonumber \]
Using the virial equation of state (Equation \ref{viral}), the Boyle temperature can be expressed in terms of the virial coefficients. Starting with the compression factor
\[Z = 1 +\dfrac{B}{V_m} + \dots \nonumber \]
and then differentiating with respect to \(1/V_m\) yields
\[\dfrac{\partial Z}{\partial \left(\frac{1}{V_m}\right)} = B \nonumber \]
So it can be concluded that at the Boyle temperature, the second virial coefficient \(B\) is equal to zero. This should make some sense given that the first virial coefficient provides most of the deviation from the ideal gas law, and so it must vanish as the gas behaves more ideally.
Critical Behavior
The isotherms (lines of constant temperature) of CO2 reveal a very large deviation from ideal behavior. At high temperatures, CO2 behaves according to Boyle’s Law. However, at lower temperatures, the gas begins to condense to form a liquid at high pressures. At one specific temperature, the critical temperature, the isotherm begins to display this critical behavior. The temperature, pressure, and molar volume (\(p_c\), \(T_c\), and \(V_c\)) at this point define the critical point. In order to solve for expressions for the critical constants, one requires three equations. The equation of state provides one relationship. The second can be generated by recognizing that the slope of the isotherm at the critical point is zero. And finally, the third expression is derived by recognizing that the isotherm passes through an inflection point at the critical point. Using the van der Waals equation as an example, these three equations can be generated as follows:
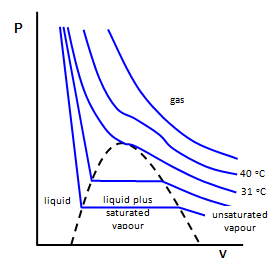
Solving these expressions for \(p_c\), \(T_c\), and \(V_c\) yields
\[p_c = \dfrac{a}{27b^2} \nonumber \]
\[T_c = \dfrac{8a}{27bR} \nonumber \]
\[V_c = 3b \nonumber \]
The critical variables can be used in this fashion to determine the values of the molecular parameters used in an equation of state (such as the van der Waals equation) for a given substance.
The Principle of Corresponding States
The principle of corresponding states was proposed by van der Waals in 1913 (van der Waals J. D., 1913). He noted that the compression factor at the critical point
\[Z_c = \dfrac{p_cV_c}{RT_c} \nonumber \]
is very nearly the same for any substance. This is consistent with what is predicted by the van der Waals equation, which predicts \(Z_c = 0.375\) irrespective of substance.
Further, it can be noted that based on reduced variables defined by
\[p_r= \dfrac{p}{p_c} \nonumber \]
\[V_r= \dfrac{V}{V_c} \nonumber \]
\[T_r= \dfrac{T}{T_c} \nonumber \]
several physical properties are found to be comparable for real substances. For example (Guggenheim, 1945), for argon, krypton, nitrogen, oxygen, carbon dioxide and methane the reduced compressibility is
\[[ \dfrac{p_cV_c}{RT_c} \approx 0.292 \nonumber \]
Also, the reduced compression factor can be plotted as a function of reduced pressure for several substances at several reduced isotherms with surprising consistency irrespective of the substance.


