2.3: The Kinetic Molecular Theory of Gases
- Page ID
- 84297
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Theoretical models attempting to describe the nature of gases date back to the earliest scientific inquiries into the nature of matter and even earlier! In about 50 BC, Lucretius, a Roman philosopher, proposed that macroscopic bodies were composed of atoms that continually collide with one another and are in constant motion, despite the observable reality that the body itself is as rest. However, Lucretius’ ideas went largely ignored as they deviated from those of Aristotle, whose views were more widely accepted at the time.
In 1738, Daniel Bernoulli (Bernoulli, 1738) published a model that contains the basic framework for the modern Kinetic Molecular theory. Rudolf Clausius furthered the model in 1857 by (among other things) introducing the concept of mean free path (Clausius, 1857). These ideas were further developed by Maxwell (Maxwell, Molecules, 1873). But, because atomic theory was not fully embraced in the early 20th century, it was not until Albert Einstein published one of his seminal works describing Brownian motion (Einstein, 1905) in which he modeled matter using a kinetic theory of molecules that the idea of an atomic (or molecular) picture really took hold in the scientific community.
In its modern form, the Kinetic Molecular Theory of gasses is based on five basic postulates.
- Gas particles obey Newton’s laws of motion and travel in straight lines unless they collide with other particles or the walls of the container.
- Gas particles are very small compared to the averages of the distances between them.
- Molecular collisions are perfectly elastic so that kinetic energy is conserved.
- Gas particles so not interact with other particles except through collisions. There are no attractive or repulsive forces between particles.
- The average kinetic energy of the particles in a sample of gas is proportional to the temperature.
Qualitatively, this model predicts the form of the ideal gas law.
- More particles means more collisions with the wall (\(p \propto n\))
- Smaller volume means more frequent collisions with the wall (\(p \propto 1/V\))
- Higher molecular speeds means more frequent collisions with the walls (\(p \propto T\))
Putting all of these together yields
\[ p \propto \dfrac{nT}{V} =k \dfrac{nT}{V} \nonumber \]
which is exactly the form of the ideal gas law! The remainder of the job is to derive a value for the constant of proportionality (\(k\)) that is consistent with experimental observation.
For simplicity, imagine a collection of gas particles in a fixed-volume container with all of the particles traveling at the same velocity. What implications would the kinetic molecular theory have on such a sample? One approach to answering this question is to derive an expression for the pressure of the gas.
The pressure is going to be determined by considering the collisions of gas molecules with the wall of the container. Each collision will impart some force. So the greater the number of collisions, the greater the pressure will be. Also, the larger force imparted per collision, the greater the pressure will be. And finally, the larger the area over which collisions are spread, the smaller the pressure will be.
\[ p \propto \dfrac{ (\text{number of collisions}) \times (\text{force imparted per collision})}{area} \nonumber \]
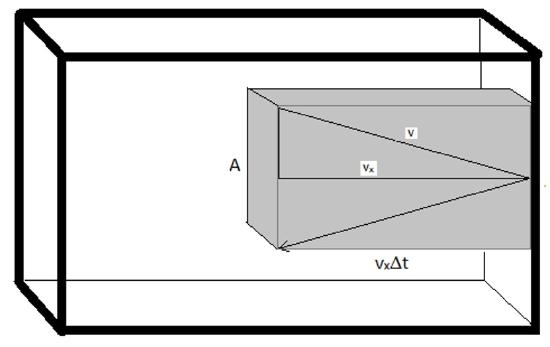
First off, the pressure that the gas exerts on the walls of the container would be due entirely to the force imparted each time a molecule collides with the interior surface of the container. This force will be scaled by the number of molecules that hit the area of the wall in a given time. For this reason, it is convenient to define a “collision volume”.
\[ V_{col}= (v_x \cdot \Delta t) \cdot A \nonumber \]
where \(v_x\) is the speed the molecules are traveling in the x direction, \(\Delta t\) is the time interval (the product of \(v_x·\Delta T\) gives the length to the collision volume box) and A is the area of the wall with which the molecules will collide. Half of the molecules within this volume will collide with the wall since half will be traveling toward it and half will be traveling away from it. The number of molecules in this collision volume will be given by the total number of molecules in the sample and the fraction of the total volume that is the collision volume. And thus, the number of molecules that will collide with the wall is given by
\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{V_{col}}{V} \nonumber \]
And thus the number of molecules colliding with the wall will be
\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{(v_x \cdot \Delta t) \cdot A}{V} \nonumber \]
The magnitude of that force imparted per collision will be determined by the time-rate of change in momentum of each particle as it hits the surface. It can be calculated by determining the total momentum change and dividing by the total time required for the event. Since each colliding molecule will change its velocity from vx to –vx, the magnitude of the momentum change is 2(mvx). Thus the force imparted per collision is given by
\[ F = \dfrac{2(mv_x)}{\Delta t} \nonumber \]
and the total force imparted is
\[\begin{align} F_{tot} &= N_{col} \dfrac{2 (mv_x)}{\Delta t} \\[4pt] &= \dfrac{1}{2} N_{tot} \left[ \dfrac{(v_x\Delta t)A}{V} \right] \left[ \dfrac{2(m v_x)}{\Delta t} \right] \\[4pt] &= N_{tot} \left(\dfrac{mv_x^2}{V} \right) A \end{align} \nonumber \]
Since the pressure is given as the total force exerted per unit area, the pressure is given by
\[p = \dfrac{F_{tot}}{A} = N_{tot} \left( \dfrac{mv_x^2}{V} \right) = \dfrac{N_{tot}m}{V} v_x^2 \nonumber \]
The question then becomes how to deal with the velocity term. Initially, it was assumed that all of the molecules had the same velocity, and so the magnitude of the velocity in the x-direction was merely a function of the trajectory. However, real samples of gases comprise molecules with an entire distribution of molecular speeds and trajectories. To deal with this distribution of values, we replace (\(v_x^2\)) with the squared average of velocity in the x direction \(\langle v_x \rangle ^2\).
\[p = \dfrac{N_{tot}m}{V} \langle v_x \rangle ^2 \label{press} \]
The distribution function for velocities in the x direction, known as the Maxwell-Boltzmann distribution, is given by:
\[f(v_x) = \underbrace{\sqrt{ \dfrac{m}{2\pi k_BT} }}_{\text{normalization term}} \underbrace{\exp \left(\dfrac{-mv_x^2}{2k_BT} \right)}_{\text{exponential term}} \nonumber \]
This function has two parts: a normalization constant and an exponential term. The normalization constant is derived by noting that
\[\int _{-\infty}^{\infty} f(v_x) dv_x =1 \label{prob} \]
The Maxwell-Boltzmann distribution has to be normalized because it is a continuous probability distribution. As such, the sum of the probabilities for all possible values of vx must be unity. And since \(v_x\) can take any value between -∞ and ∞, then Equation \ref{prob} must be true. So if the form of \(f(v_x)\) is assumed to be
\[f(v_x) = N \exp - \left(\dfrac{mv_x^2}{2k_BT} \right) \nonumber \]
The normalization constant \(N\) can be found from
\[ \int_{-\infty}^{\infty} f(v_x) dv_x = \int_{-\infty}^{\infty} N \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1 \nonumber \]
The expression can be simplified by letting \(\alpha = m/2k_BT\). It is then more simply written
\[ N \int_{-\infty}^{\infty} \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1 \nonumber \]
A table of definite integrals says that
\[ \int_{-\infty}^{\infty} e^{- a x^2} dx = \sqrt{\dfrac{\pi}{a}} \nonumber \]
So
\[ N \sqrt{\dfrac{\pi}{\alpha}} = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \nonumber \]
And thus the normalized distribution function is given by
\[ f(v_x) = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \text{exp} \left( \dfrac{m v_x^2}{2 k_BT} \right) \label{MB} \]
Calculating an average for a finite set of data is fairly easy. The average is calculated by
\[ \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i \nonumber \]
But how does one proceed when the set of data is infinite? Or how does one proceed when all one knows are the probabilities for each possible measured outcome? It turns out that that is fairly simple too!
\[ \bar{x} = \sum_{i=1}^N x_i P_i \nonumber \]
where \(P_i\) is the probability of measuring the value \(x_i\). This can also be extended to problems where the measurable properties are not discrete (like the numbers that result from rolling a pair of dice) but rather come from a continuous parent population. In this case, if the probability is of measuring a specific outcome, the average value can then be determined by
\[\bar{x} = \int x P(x) dx \nonumber \]
where \(P(x)\) is the function describing the probability distribution, and with the integration taking place across all possible values that x can take.
A value that is useful (and will be used in further developments) is the average velocity in the x direction. This can be derived using the probability distribution, as shown in the mathematical development box above. The average value of \(v_x\) is given by
\[ \langle v_x \rangle = \int _{-\infty}^{\infty} v_x (f(v_x) dx \nonumber \]
This integral will, by necessity, be zero. This must be the case as the distribution is symmetric, so that half of the molecules are traveling in the +x direction, and half in the –x direction. These motions will have to cancel. So, a more satisfying result will be given by considering the magnitude of \(v_x\), which gives the speed in the x direction. Since this cannot be negative, and given the symmetry of the distribution, the problem becomes
\[ \langle |v_x |\rangle = 2 \int _{0}^{\infty} v_x (f(v_x) dx \nonumber \]
In other words, we will consider only half of the distribution, and then double the result to account for the half we ignored.
For simplicity, we will write the distribution function as
\[ f(v_x) = N \exp(-\alpha v_x^2) \nonumber \]
where
\[ N= \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \nonumber \]
and
\[\alpha = \dfrac{m}{2k_BT}. \nonumber \]
A table of definite integrals shows
\[ \int_{0}^{\infty} x e^{- a x^2} dx = \dfrac{1}{2a} \nonumber \]
so
\[ \langle v_x \rangle = 2N \left( \dfrac{1}{2\alpha}\right) = \dfrac{N}{\alpha} \nonumber \]
Substituting our definitions for \(N\) and \(\alpha\) produces
\[ \langle v_x \rangle = \left( \dfrac{m}{2\pi k_BT} \right)^{1/2} \left( \dfrac{2 k_BT}{m} \right) = \left( \dfrac{2\pi k_BT}{ \pi m} \right)^{1/2} \nonumber \]
This expression indicates the average speed for motion of in one direction.
However, real gas samples have molecules not only with a distribution of molecular speeds and but also a random distribution of directions. Using normal vector magnitude properties (or simply using the Pythagorean Theorem), it can be seen that
\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2 \nonumber \]
Since the direction of travel is random, the velocity can have any component in x, y, or z directions with equal probability. As such, the average value of the x, y, or z components of velocity should be the same. And so
\[ \langle v \rangle^2 = 3 \langle v_x \rangle^2 \nonumber \]
Substituting this into the expression for pressure (Equation \ref{press}) yields
\[ p =\dfrac{ N_{tot}m}{3V} \langle v \rangle^2 \nonumber \]
All that remains is to determine the form of the distribution of velocity magnitudes the gas molecules can take. One of the first people to address this distribution was James Clerk Maxwell (1831-1879). In his 1860 paper (Maxwell, Illustrations of the dynamical theory of gases. Part 1. On the motions and collisions of perfectly elastic spheres, 1860), proposed a form for this distribution of speeds which proved to be consistent with observed properties of gases (such as their viscosities). He derived this expression based on a transformation of coordinate system from Cartesian coordinates (\(x\), \(y\), \(z\)) to spherical polar coordinates (\(v\), \(\theta\), \(\phi\)). In this new coordinate system, v represents the magnitude of the velocity (or the speed) and all of the directional data is carried in the angles \(\theta\) and \(\phi\). The infinitesimal volume unit becomes
\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi \nonumber \]
Applying this transformation of coordinates, and ignoring the angular part (since he was interested only in the speed) Maxwell’s distribution (Equation \ref{MB}) took the following form
\[ f(v) = N v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFullN} \]
This function has three basic parts to it: a normalization constant (\(N\)), a velocity dependence (\(v^2\)), and an exponential term that contains the kinetic energy (\(½ mv^2\)). Since the function represents the fraction of molecules with the speed \(v\), the sum of the fractions for all possible velocities must be unity. This sum can be calculated as an integral. The normalization constant ensures that
\[ \int_0^{\infty} f(v) dv = 1 \nonumber \]
Choosing the normalization constant as
\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \nonumber \]
yields the final form of the Maxwell distribution of molecular speeds.
\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFull} \]
At low velocities, the \(v^2\) term causes the function to increase with increasing \(v\), but then at larger values of \(v\), the exponential term causes it to drop back down asymptotically to zero. The distribution will spread over a larger range of speed at higher temperatures, but collapse to a smaller range of values at lower temperatures (Table 2.3.1).
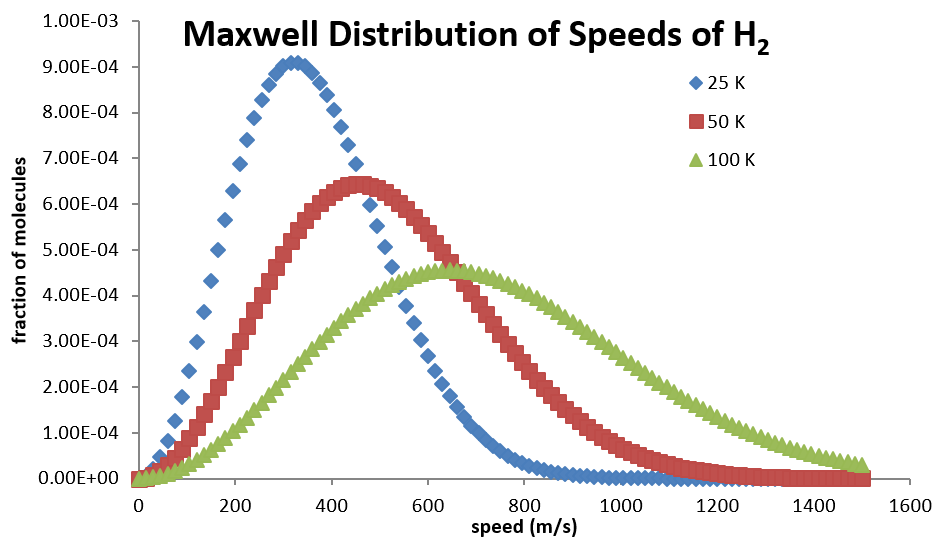
Using the Maxwell distribution as a distribution of probabilities, the average molecular speed in a sample of gas molecules can be determined.
\[ \begin{align} \langle v \rangle & = \int _{-\infty}^{\infty} v \,f(v) dv \\ & = \int _{-\infty}^{\infty} v\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^3 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align} \nonumber \]
The following can be found in a table of integrals:
\[ \int_0^{\infty} x^{2n+1} e^{-ax^2} dx = \dfrac{n!}{2a^{n+1}} \nonumber \]
So
\[\langle v \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1}{2 \left( \dfrac{m}{2 k_B T} \right) ^2 } \right] \nonumber \]
Which simplifies to
\[\langle v \rangle = \left( \dfrac{8 k_BT}{\pi m} \right) ^{1/2} \nonumber \]
Note: the value of \(\langle v \rangle \) is twice that of \(\langle v_x \rangle \) which was derived in an earlier example!
\[\langle v \rangle = 2\langle v_x \rangle \nonumber \]
What is the average value of the squared speed according to the Maxwell distribution law?
Solution
\[ \begin{align} \langle v^2 \rangle & = \int _{-\infty}^{\infty} v^2 \,f(v) dv \\ & = \int _{-\infty}^{\infty} v^2\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^4 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align} \nonumber \]
A table of integrals indicates that
\[ \int_0^{\infty} x^{2n} e^{-ax^2} dx = \dfrac{1 \cdot 3 \,cdot 5 \dots (2n-1)}{2^{n+1}a^n} \sqrt{\dfrac{\pi}{a}} \nonumber \]
Substitution (noting that \(n = 2\)) yields
\[\langle v^2 \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1 \cdot 3}{2^3 \left( \dfrac{m}{2 k_BT} \right) ^2 } \sqrt{\dfrac{\pi}{\left( \dfrac{m}{2 k_BT} \right)}} \right] \nonumber \]
which simplifies to
\[\langle v^2 \rangle = \dfrac{3 k_BT}{ m} \nonumber \]
Note: The square root of this average squared speed is called the root mean square (RMS) speed, and has the value
\[v_{rms} = \sqrt{ \langle v^2 \rangle } = \left( \dfrac{3 k_BT}{ m} \right)^{1/2} \nonumber \]
The entire distribution is also affected by molecular mass. For lighter molecules, the distribution is spread across a broader range of speeds at a given temperature, but collapses to a smaller range for heavier molecules (Table 2.3.2).
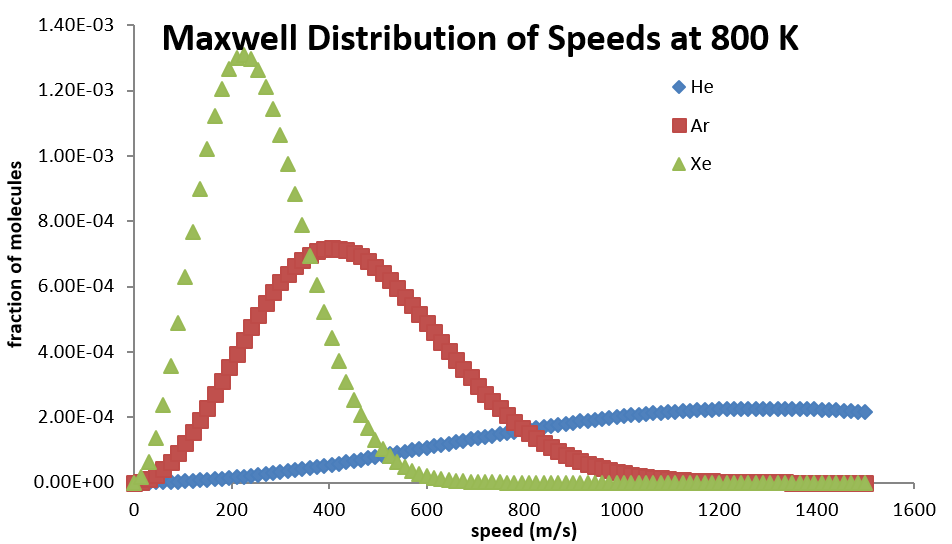
The probability distribution function can also be used to derive an expression for the most probable speed (\(v_{mp}\)), the average (\(v_{ave}\)), and the root-mean-square (\(v_{rms}\)) speeds as a function of the temperature and masses of the molecules in the sample. The most probable speed is the one with the maximum probability. That will be the speed that yields the maximum value of \(f(v)\). It is found by solving the expression
\[ \dfrac{d}{dv} f(v) = 0 \nonumber \]
for the value of \(v\) that makes it true. This will be the value that gives the maximum value of \(f(v)\) for the given temperature. Similarly, the average value can be found using the distribution in the following fashion
\[ v_{ave} = \langle v \rangle \nonumber \]
and the root-mean-square (RMS) speed by finding the square root of the average value of \(v^2\). Both demonstrated above.
\[ v_{rms} = \sqrt{ \langle v^2 \rangle} \nonumber \]


