1.5: Work and Energy
- Page ID
- 84292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Temperature, pressure and volume are important variables in the description of physical systems. They will also be important to describe how energy flows from one system to another. Generally, energy can flow in two important forms: 1) work and 2) heat. The bookkeeping needed to track the flow of energy is what the subject of Thermodynamics is all about, so these topics will be discussed at length in subsequent chapters. However, a little bit of review is in order, just to set the foundation for the discussions that are forthcoming.
Energy
Energy is an important entity in the modern world. We use energy to light our homes, drive our cars, and power our electronic devices. According to Richard Smalley, co-winner of the 1996 Nobel Prize in Chemistry, energy is one of the (if not the biggest) challenge we face moving into the 21st century (energy.senate.gov, 2004):
Energy is at the core of virtually every problem facing humanity. We cannot afford to get this wrong. … Somehow we must find the basis for energy prosperity for ourselves and the rest of humanity for the 21st century. By the middle of this century we should assume we will need to at least double world energy production from its current level, with most of this coming from some clean, sustainable, CO2-free source. For worldwide peace and prosperity it needs to be cheap.- Richard Smalley, Testimony to the Senate Committee on Energy and Natural Resources, April 26, 2004
Energy can be measured in a multitude of different units, including joules (J), kilojoules (kJ), calories (cal), kilocalories (kcal), as well as several other set of units such as kJ/mol or kcal/mol.
A calorie (cal) was once defined as the amount of energy needed to raise the temperature of 1 g of water by 1 °C. This definition suggests a convenient property of water called the specific heat:
\[C = \dfrac{1\,cal}{g\, °C} \nonumber \]
The modern definition of a calorie is 4.184 joule,
\[ 1 \,J = 1\,N \cdot m = \dfrac{1 \,kg \, m^2}{s^2} \nonumber \]
where a joule is the energy necessary to move a mass a distance of 1 m against a resisting force of 1 N.
A dietary Calorie (Cal) is equal to 1000 cal, or 1 kcal, and is often listed on the labels of food containers to indicate the energy content of the food inside.
Energy can take the form of potential energy (stored energy) and kinetic energy (realized energy) forms. Kinetic energy is the energy of motion. On the other hand, potential energy can be defined as the energy stored in a system that can be converted to kinetic energy someplace in the universe. Kinetic energy of a particle can be expressed as
\[E_{kin} = \dfrac{1}{2} mv^2 \label{transKE} \]
where \(m\) is the mass of the particle, and \(v\) is the magnitude of its velocity (or speed). Equation \ref{transKE} describes the kinetic energy associated with translation; other expressions exist for different motions (e.g., rotation or vibration).
An example of a system in which energy is converted between kinetic energy and potential energy is a Hooke’s Law oscillator. According to Hooke’s Law, the force acting on an object is proportional in magnitude to the displacement of the object from an equilibrium position, and opposite in sign.
\[ F = -kx \label{hook} \]
In this equation, \(F\) is the force, \(x\) is the displacement from equilibrium, and \(k\) is the constant of proportionality. The negative sign is necessary to insure that the force acting on the object is one that will tend to restore it to an equilibrium position (\(x = 0\)) irrespective of whether \(x\) is positive or negative.
As the object that follows Hooke’s Law moves from its equilibrium position, the kinetic energy of its motion is converted into potential energy until there is no more kinetic energy left. At this point, the change in displacement will change direction, returning the object to the equilibrium position by converting potential energy back into kinetic energy.
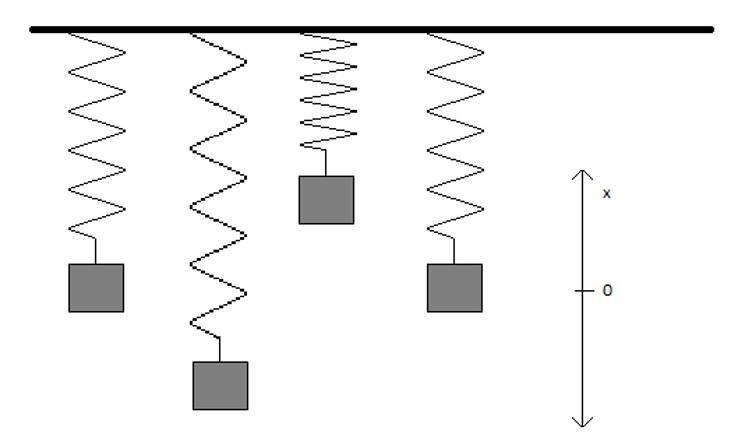
As the object is displaced in the along the x-axis (in the case shown in Figure 1.5.1, this would be accomplished by stretching or compressing the spring), the potential energy increases. The force acting on the object will also increase as the object is displaced and will be directed opposite of the direction of displacement (Equation \ref{hook}). According to Newtonian physics, the potential energy \(U(x)\) is given by the negative integral of the force with respect to position:
\[U (x) = - \int F(x) dx \label{energy} \]
Substituting Equation \ref{hook} in Equation \ref{energy} yields
\[U(x) = - \int (-k x)dx \nonumber \]
\[ = \dfrac{1}{2} kx^2 + constant \nonumber \]
With the proper choice of coordinate system and other definitions, the constant of integration can be arbitrarily made to be zero (for example, by choosing it to offset any other forces acting on the object, such as the force due to gravity.) The kinetic energy is then given by the total energy minus the potential energy (since the total energy must be constant due to the conservation of energy in the system!)
\[ E_{kin} = E_{tot} -U(x) \nonumber \]
Work
Work is defined as the amount of energy expended to move a mass against a resisting force. For a mass being moved along a surface, the amount of energy expended must be sufficient to overcome the resisting force (perhaps due to friction) and also sufficient to cause motion along the entire path.
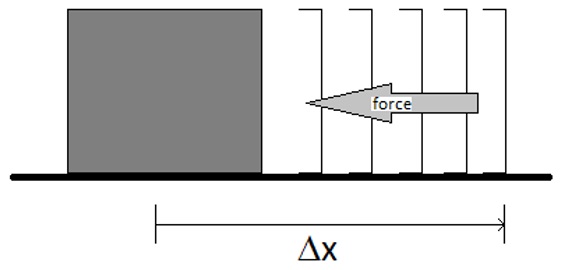
The energy expended as work in this case (if the force is independent of the position of the object being moved) is given by
\[w= - F \,\Delta x \nonumber \]
where F is the magnitude of the resisting force, and Dx is the displacement of the object. The negative sign is necessary since the force is acting in the opposite direction of the motion. A more general expression, and one that can be used if the force is not constant over the entire motion is
\[ dw = -F \,dx \nonumber \]
This expression can then be integrated, including any dependence \(F\) might have on \(x\) as needed for a given system.
Another important way that work can be defined includes that for the expansion of a gas sample against an external pressure. In this case, the displacement is defined by a change in volume for the sample:
\[dw = -p_{ext} dV \nonumber \]
This is a very convenient expression and will be used quite often when discussing the work expended in the expansion of a gas.
The conversion of potential energy into kinetic energy generally is accomplished through work which is done someplace in the universe. As such, the concepts of energy and work are inexorably intertwined. They will be central to the study of thermodynamics.
The work of a “reversible” expansion
An important case of limiting ideal behavior[1] is that of the reversible expansion. For a change to be reversible there can be no net force pushing the change in one direction or the other. In order for this to be the case, the internal pressure (that of the system) and external pressure (that of the surroundings) must be the same.
\[p_{int} = p_{ext} = p \nonumber \]
In this case, the work of expansion can be calculated by integrating the expression for dw.
\[w = \int dw = -\int p dV \nonumber \]
Making a simple substitution from the ideal gas law
\[p=\dfrac{nRT}{V} \label{IGL} \]
allows for the expression in terms of volume and temperature. If the temperature is constant (so that it can be placed before the integral) the expression becomes
\[w= - nRT \int_{V_1}^{V_2} \dfrac{dV}{V} = -nRT \ln \left( \dfrac{V_2}{V_1} \right) \label{workIG} \]
where \(V_1\) and \(V_2\) are the initial and final volumes of the expansion respectively.
Consider 1.00 mol of an ideal gas, expanding isothermally at 273 K, from an initial volume of 11.2 L to a final volume of 22.4 L. What is the final pressure of the gas? Calculate the work of the expansion if it occurs
- against a constant external pressure equal to the final pressure you have calculated.
- reversibly.
Solution
First, let’s calculate the final pressure via Equation \ref{IGL}:
\[ p = \dfrac{nRT}{V} = \dfrac{(1.00\,mole)(0.08206\, atm\,L\,mol^{-1} K^{-1})(273\,K)}{22.4\, L} = 1.00 \, atm \nonumber \]
(This may be a relationship you remember from General Chemistry – that 1 mole of an idea gas occupies 22.4 L at 0 oC!)
Okay – now for the irreversible expansion against a constant external pressure:
\[dw = -p_{ext}dV \nonumber \]
so
\[w = -p_{exp} \int _{V_1}^{V_2} dV = -p_{ext} \Delta V \nonumber \]
\[ w = -(1.00 \, atm)(22.4 \, L- 11.2\,L) =-11.2 \,atm\,L \nonumber \]
But what the heck is an atm L? It is actually a fairly simply thing to convert from units of atm L to J by using the ideal gas law constant.
\[w = -(11.2 \,atm\,L) \left( \dfrac{8.314\, \frac{J}{mol\, K}}{0.08206\, \frac{atm\, L}{mol\, K}} \right) = -1130 \,J \nonumber \]
Note that the negative sign indicated that the system is expending energy by doing work on the surroundings. (This concept will be vital in the Chapter 3!)
Now for the reversible pathway. The work done by the system can be calculated for this change using Equation \ref{workIG}:
\[w= -(1.00\, mol) (8.314 J\, mol^{-1} K^{-1}) (273 \,K) \ln \left( \dfrac{22.4\,L}{11.2\,L} \right) = -1570\,J \nonumber \]
Notes:
- First notice how the value for the gas law constant, R, was chosen in order to match the units required in the problem. (Read and recite that previous sentence to yourself a few times. The incorrect choice of the value of R is one of the most common errors made by students in physical chemistry! By learning how the units will dictate your choice of R, you will save yourself a considerable number of headaches as you learn physical chemistry!)
- Second, You may note that the magnitude of work done by the system in the reversible expansion is larger than that of the irreversible expansion. This will always be the case!
[1] There are many cases of “limiting ideal behavior” which we use to derive and/or explore the nature of chemical systems. The most obvious case, perhaps, is that of the Ideal Gas Law.


