15.4: Symmetry Operators
- Page ID
- 106899
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The symmetry of molecules is essential for understanding the structures and properties of organic and inorganic compounds. The properties of chemical compounds are often easily explained by consideration of symmetry. For example, the symmetry of a molecule determines whether the molecule has a permanent dipole moment or not. The theories that describe optical activity, infrared and ultraviolet spectroscopy, and crystal structure involve the application of symmetry considerations. Matrix algebra is the most important mathematical tool in the description of symmetry.
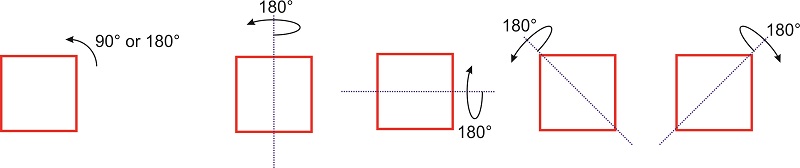
A symmetry operation, such as a rotation around a symmetry axis or a reflection through a plane, is an operation that, when performed on an object, results in a new orientation of the object that is indistinguishable from the original. For example, if we rotate a square in the plane by \(\pi/2\) or \(\pi\) the new orientation of the square is superimposable on the original one (Figure \(\PageIndex{1}\)).
If rotation by an angle \(\theta\) of a molecule (or object) about some axis results in an orientation of the molecule (or object) that is superimposable on the original, the axis is called a rotation axis. The molecule (or object) is said to have an \(n\)-fold rotational axis, where \(n\) is \(2\pi/\theta\). The axis is denoted as \(C_n\). The square of Figure \(\PageIndex{1}\) has a \(C_4\) axis perpendicular to the plane because a \(90^{\circ}\) rotation leaves the figure indistinguishable from the initial orientation. This axis is also a \(C_2\) axis because a \(180^{\circ}\) degree rotation leaves the square indistinguishable from the original square. In addition, the figure has several other \(C_2\) axis that lie on the same plane as the square:
A symmetry operation moves all the points of the object from one initial position to a final position, and that means that symmetry operators are \(3\times 3\) square matrices (or \(2\times 2\) in two dimensions). The following equation represents the action of a symmetry operator \(\hat A\) on the location of the point \((x,y,z)\) (a vector):
\[\hat A (x,y,z)=(x',y',z') \nonumber \]
The vector \((x',y',z')\) represents the location of the point after the symmetry operation. Let’s come back to the rotation axes we discussed before. A 2-fold rotation around the \(z-\)axis changes the location of a point \((x,y,z)\) to \((-x,-y,z)\) (see Figure \(\PageIndex{2}\)). By convention, rotations are always taken in the counterclockwise direction.
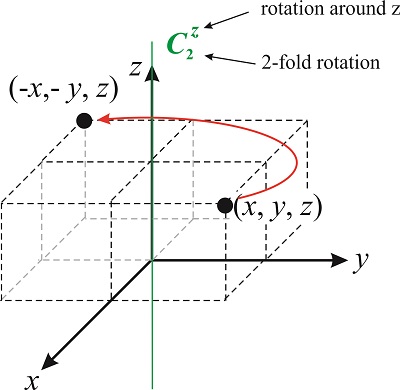
What is the matrix that represents the operator \(\hat {C^z_2}\)? The matrix transforms the vector \((x,y,z)\) into \((-x,-y,z)\), so
\[\hat {C^z_2}(x,y,z)=(-x,-y,z) \nonumber \]
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} -x \\ -y \\ z \end{pmatrix} \nonumber \]
We know the matrix is a \(3\times 3\) square matrix because it needs to multiply a 3-dimensional vector. In addition, we write the vector as a vertical column to satisfy the requirements of matrix multiplication.
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} \nonumber \]
\[a_{11}x+a_{12}y+a_{13}z=-x \nonumber \]
\[a_{21}x+a_{22}y+a_{23}z=-y \nonumber \]
\[a_{31}x+a_{32}y+a_{33}z=z \nonumber \]
and we conclude that \(a_{11}=-1\), \(a_{12}=a_{13}=0\), \(a_{22}=-1\), \(a_{21}=a_{23}=0\) and \(a_{33}=1\), \(a_{31}=a_{32}=0\):
\[\hat{C^z_2}=\begin{pmatrix} -1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
Rotations are not the only symmetry operations we can perform on a molecule. Figure \(\PageIndex{3}\) illustrates the reflection of a point through the \(xz\) plane. This operation transforms the vector \((x,y,z)\) into the vector \((x,-y,z)\). Symmetry operators involving reflections through a plane are usually denoted with the letter \(\sigma\), so the operator that reflects a point through the \(xz\) plane is \(\hat{\sigma}_{xz}\):
\[\hat{\sigma}_{xz}(x,y,z)=(x,-y,z) \nonumber \]
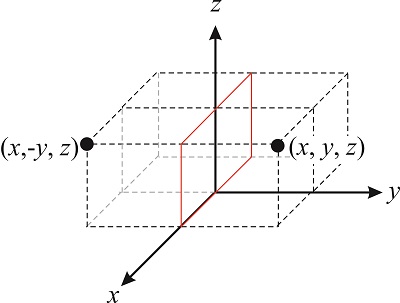
Following the same logic we used for the rotation matrix, we can write the \(\hat{\sigma}_{xz}\) operator as:
\[\hat{\sigma}_{x,z}=\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
This is true because
\[\begin{pmatrix} 1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} x \\ -y \\ z \end{pmatrix} \nonumber \]
As we said before, the symmetry properties of molecules are essential for understanding the structures and properties of organic and inorganic compounds. For example, those of you who took organic chemistry know that molecules that have an inversion center (Problem 15.3) do not have permanent dipole moments. The symmetry of molecules is also related to their abilities to absorb light. Figure \(\PageIndex{4}\) shows the three symmetry elements of the molecule of water (H\(_2\)O). This molecule has only one rotation axis, which is 2-fold, and therefore we call it a “\(C_2\) axis”. It also has two mirror planes, one that contains the two hydrogen atoms (\(\sigma_{yz}\)), and another one perpendicular to it (\(\sigma_{xz}\)). Both planes contain the C\(_2\) axis.
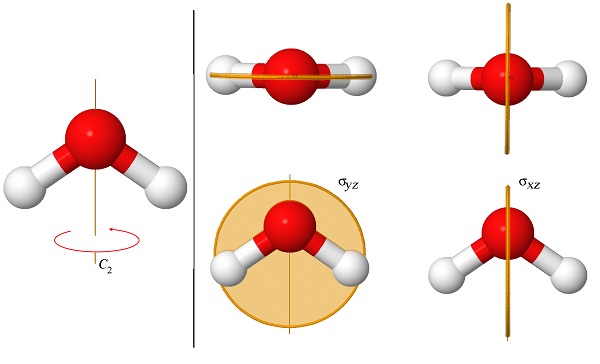
As you will learn in your inorganic chemistry course, chemists organize molecules that share the same symmetry elements under a common group. For example, the group that contains molecules with these three symmetry elements is called “the \(C_{2v}\) group”. Because the inversion operation (Problem 15.3) is not part of this group we know that all \(C_{2v}\) molecules are polar.
The molecule of methane (CH\(_4\)) has several symmetry elements, some of which we have not learned in this chapter. One that is relatively easy to identify is the C\(_3\) rotation axis (Figure \(\PageIndex{5}\)):
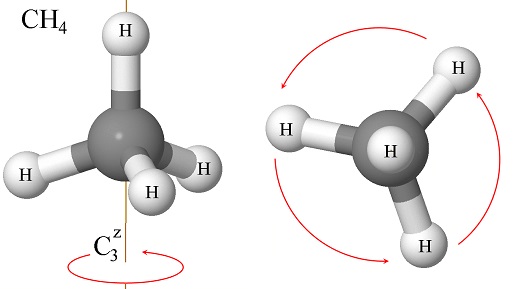
Can we write the matrix for the operator that corresponds to the 3-fold rotation? If we look at the molecule from the top, so the \(z\)-axis is perpendicular to the plane of the paper (or screen if you are reading this in a computer), we see that the rotation moves one hydrogen atom from one vertex of an equilateral triangle to the other one in a counterclockwise fashion. Therefore, we need a matrix that will move these vertices as shown in the figure:
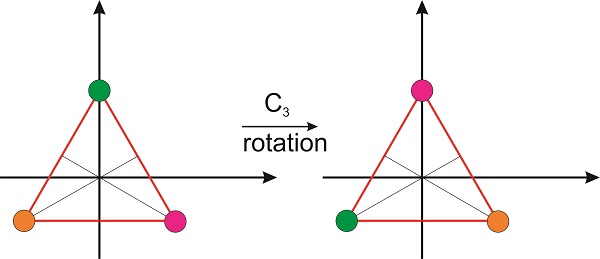
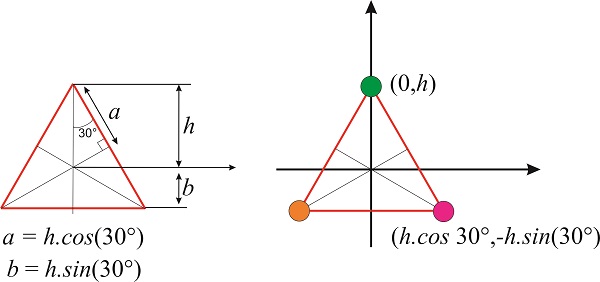
We need the coordinates of the three vertices, which can be obtained from simple geometrical arguments. If we place the green vertex at \(x=0\) and \(y=h\), then the position of the magenta vertex is \(x=h\times \cos 30^{\circ}\) and \(y=-h\times \sin 30^{\circ}\) and the position of the orange vertex is \(-x=h\times \cos 30^{\circ}\) and \(y=-h\times \sin 30^{\circ}\) (Figure \(\PageIndex{7}\)).
The matrix we are looking for needs to rotate the magenta circle until it overlaps with the green circle:
\[\hat {C}_3(h \sqrt{3}/2,-h/2,z)=(0,h,z) \nonumber \]
where we note that this rotation does not change the value of \(z\).
\[\begin{pmatrix} a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23} \\ a_{31}&a_{32}&a_{33} \end{pmatrix}\begin{pmatrix} h\sqrt{3}/2 \\ -h/2\\ z\end{pmatrix}=\begin{pmatrix} 0 \\ h \\ z \end{pmatrix} \nonumber \]
Here, we have used the fact that \(\cos30^{\circ}=\sqrt{3}/2\) and \(\sin 30^{\circ}=1/2\).
Multiplying the matrix by the vector:
\[a_{11}h\sqrt{3}/2-a_{12}h/2+a_{13}z=0 \nonumber \]
\[a_{21}h\sqrt{3}/2-a_{22}h/2+a_{23}z=h \nonumber \]
\[a_{31}h\sqrt{3}/2-a_{32}h/2+a_{33}z=z \nonumber \]
From these equations, we conclude that \(a_{13}=a_{23}=a_{31}=a_{32}=0\), \(a_{12}=\sqrt{3}a_{11}\), and \(a_{22}=\sqrt{3}a_{21}-2\). So far the matrix looks like:
\[\hat {C}_3=\begin{pmatrix} a_{11}&\sqrt{3}a_{11}&0 \\ a_{21}&\sqrt{3}a_{21}-2&0 \\ 0&0&1 \end{pmatrix} \nonumber \]
To find the remaining entries let’s apply the matrix to the vector \((0,h,z)\), which needs to rotate to \((-h \sqrt{3}/2,-h/2,z)\):
\[\begin{pmatrix} a_{11}&\sqrt{3}a_{11}&0 \\ a_{21}&\sqrt{3}a_{21}-2&0 \\ 0&0&1 \end{pmatrix}\begin{pmatrix} 0 \\ h \\ z \end{pmatrix}=\begin{pmatrix} -h \sqrt{3}/2 \\ -h/2 \\ z \end{pmatrix} \nonumber \]
From this multiplication we get
\[\sqrt{3}a_{11}h=-h\sqrt{3}/2\rightarrow a_{11}=-1/2 \nonumber \]
\[(\sqrt{3}a_{21}-2)h=-h/2\rightarrow a_{21}=\sqrt{3}/2 \nonumber \]
and therefore,
\[\hat {C}_3=\begin{pmatrix} -1/2&-\sqrt{3}/2&0 \\ \sqrt{3}/2&-1/2&0 \\ 0&0&1 \end{pmatrix} \nonumber \]


