12.4: Electronegativity and Dipole Moment
- Page ID
- 41382
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Within a group of the periodic table, bond lengths tend to increase with increasing atomic number \(Z\). Consider the Group 17 elements:
\[\begin{align*}& F_2 \;\;\;\; d=141.7 \;pm\\ & Cl_2 \;\;\;\; d=199.1 \, pm \\ & Br_2 \;\;\;\; d=228.6 \, pm\\ & I_2 \;\;\;\; d=266.9 \, pm\end{align*}\]
which corresponds to an increased valence shell size, hence increased electron-electron repulsion. An important result from experiment, which has been corroborated by theory, is that bond lengths tend not to vary much from molecule to molecule. Thus, a \(CH\) bond will have roughly the same value in methane, \(CH_4\) as it will in aspirin, \(C_9 H_8 O_4\).
Bond dissociation energies. \(\Delta E_d\) measured in \(kJ/mol\), measure the energy required to break a mole of a particular kind of bond. A similar periodic trend exists for bond dissociation energies. Consider the hydrogen halides:
\[\begin{align*} & HF \;\;\;\; \Delta E_d =565 \ kJ/mol \;\;\;\; d= 0.926 \ \, pm\\ & HCl \;\;\;\; \Delta E_d =429 \ kJ/mol \;\;\;\; d= 128.4 \ \, pm\\ & HBr \;\;\;\; \Delta E_d =363 \ kJ/mol \;\;\;\; d= 142.4 \ \, pm\\ & HI \;\;\;\; \Delta E_d =295 \ kJ/mol \;\;\;\; d= 162.0 \ \, pm \end{align*}\]
Thus, as bond lengths increase with increasing \(Z\), there is a corresponding decrease in the bond dissociation energy.
\(CC\) bonds are an exception to the the rule of constancy of bond lengths across different molecules. Because \(CC\) bonds can be single, double, or triple bonds, some differences can occur. For example, consider the \(CC\) bond in the molecules ethane \((C_2 H_6)\), ethylene \((C_2 H_4)\) and acetylene \((C_2 H_2)\):
\[\begin{align*} & C_2 H_6 \;\;\;\; (single)\;\;\;\; d=1.536 \ \stackrel{\circ}{A}\;\;\;\; \Delta E_d=345 \ kJ/mol\\ & C_2 H_4 \;\;\;\; (double)\;\;\;\; d=133.7 \, pm\;\;\;\; \Delta E_d=612 \ kJ/mol\\ & C_2 H_2 \;\;\;\; (triple)\;\;\;\; d=126.4 \, pm\;\;\;\; \Delta E_d=809 \ kJ/mol\end{align*}\]
The greater the bond order, i.e., number of shared electron pairs, the greater the dissociation energy. The same will be true for any kind of bond that can come in such different ``flavors'', e.g., \(NN\) bonds, \(OO\) bonds, \(NO\) bonds, \(CO\) bonds, etc.
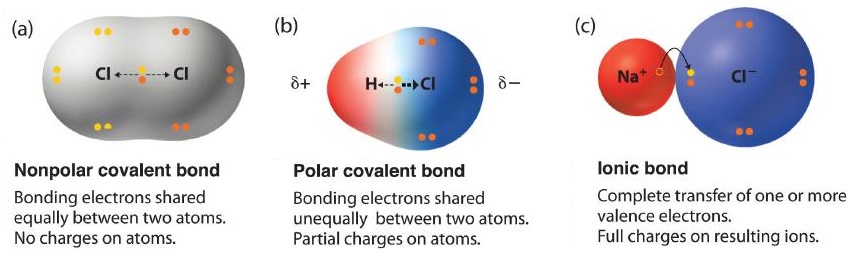
The two idealized extremes of chemical bonding:
- Ionic bonding—in which one or more electrons are transferred completely from one atom to another, and the resulting ions are held together by purely electrostatic forces—and
- Covalent bonding, in which electrons are shared equally between two atoms.
Most compounds, however, have polar covalent bonds, which means that electrons are shared unequally between the bonded atoms. Figure \(\PageIndex{1}\) compares the electron distribution in a polar covalent bond with those in an ideally covalent and an ideally ionic bond. Recall that a lowercase Greek delta (\(δ\)) is used to indicate that a bonded atom possesses a partial positive charge, indicated by \(δ^+\), or a partial negative charge, indicated by \(δ^−\), and a bond between two atoms that possess partial charges is a polar bond.
Most real chemical bonds in nature are neither truly covalent nor truly ionic. Only homonuclear bonds are truly covalent, and nearly perfect ionic bonds can form between group I and group VII elements, for example, KF. Generally, however, bonds are partially covalent and partially ionic, meaning that there is partial transfer of electrons between atoms and partial sharing of electrons. To quantify how much ionic character (and how much covalent character) a bond possesses, electronegativity differences between the atoms in the bond can be used. In 1936, Linus Pauling came up a method for estimating atomic electronegativities forms the basis of our understanding of electronegativity today.
Only homonuclear bonds are truly covalent, or as covalent as a bond can get. As discussed in Section 12.2, a quantum-mechanical treatment has shown that the two ionic structures (e.g., \(H^+H^−\) and \(H^−H^+\) for \(H_2\)) also contribute via a resonance with the covalent structure \(H−H\). However, this is often to a small extent, for example in \(H_2\), each ionic structure contributes only ~2% to the bonding of the molecule.
Pauling Electronegativity
Linus Pauling described electronegativity as “the power of an atom in a molecule to attract electrons to itself.” Basically, the electronegativity of an atom is a relative value of that atom's ability to attract election density toward itself when it bonds to another atom. The higher the electronegative of an element, the more that atom will attempt to pull electrons towards itself and away from any atom it bonds to. The main properties of an atom dictate it's electronegativity are it's atomic number as well as its atomic radius. The trend for electronegativity is to increase as you move from left to right and bottom to top across the periodic table. This means that the most electronegative atom is Fluorine and the least electronegative is Francium.
Recall the Mulliken's method was based on the arithmetic average of the first ionization energy \(IE_1\) and the electron affinity \(EA\). Both of these energies are properties of individual atoms, hence this method is appealing in its simplicity. However, there is no information about bonding in the Mulliken method. Pauling's method includes such information, and hence is a more effective approach.
To see how the Pauling method works, consider a diatomic \(AB\), which is polar covalent. Let \(\Delta E_{AA}\) and \(\Delta E_{BB}\) be the dissociation energies of the diatomics \(A_2\) and \(B_2\), respectively. Since \(A_2\) and \(B_2\) are purely covalent bonds, these two dissociation energies can be used to estimate the pure covalent contribution to the bond \(AB\). Pauling proposed the geometric mean of \(\Delta E_{AA}\) and \(\Delta E_{BB}\), this being more sensitive to large differences between these energies than the arithmetic average:
If \(\Delta E_{AB}\) is the true bond dissociation energy, then the difference
is a measure of the ionic contribution. Let us define this difference to be \(\Delta\):
\[\Delta =\Delta E_{AB}-\sqrt{\Delta E_{AA} \Delta E_{BB}}\]
Then Pauling defined the electronegativity difference \(\chi_A -\chi_B\) between atoms \(A\) and \(B\) to be
where \(\Delta\) is measured in \(kJ/mol\), and the constant \(0.102\) has units \(mol^{1/2} /kJ^{1/2}\), so that the electronegativity difference is dimensionless. Thus, with some extra input information, he was able to generate a table of atomic electronegativities that are still used today and is Tablated in Table A2 (Figure \(\PageIndex{2}\)).
To use the electronegativities to estimate degree of ionic character, simply compute the absolute value of the difference for the two atoms in the bond. As an example, consider again the hydrogen halides:
\[\begin{align*} & HF \;\;\;\; |\chi_F -\chi_H|=1.78\\ & HCl \;\;\;\; |\chi_{Cl} -\chi_H|=0.96\\ & HBr \;\;\;\; |\chi_{Br} -\chi_H|=0.76\\ & HI \;\;\;\; |\chi_I -\chi_H|=0.46\end{align*}\]
As the electronegativity difference decreases, so does the ionic character of the bond. Hence its covalent character increases. It is possible to predict whether a given bond will be non-polar, polar covalent, or ionic based on the electronegativity difference, since the greater the difference, the more polar the bond (Figure \(\PageIndex{3}\))
| Electronegativity difference, ΔχP | Bond |
|---|---|
| Δχ < 0.4 | covalent |
| 0.4 < Δχ < 1.7 | polar covalent |
| Δχ > 1.7 | ionic |
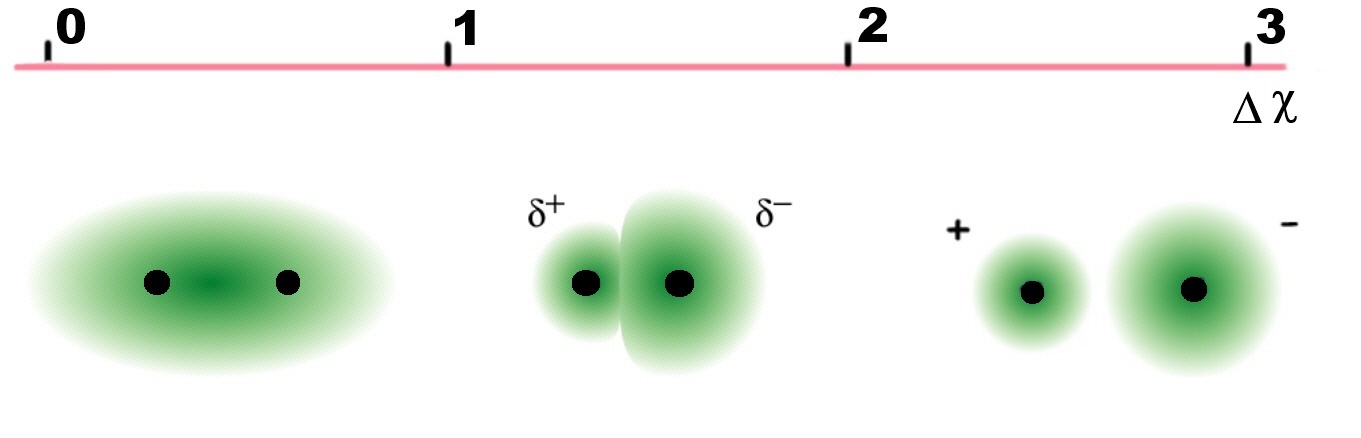
As the electronegativity difference decreases, so does the ionic character of the bond. Hence its covalent character increases.
Dipole moment
In a nearly perfect ionic bond, such as \(KF\), where electron transfer is almost complete, representing the molecule as
is a very good approximation, since the charge on the potassium will be approximately \(1e\) and the charge on the fluorine will be approximately \(-1e\). For a polar covalent bond, such as \(HF\), in which only partial charge transfer occurs, a more accurate representation would be
where \(\delta\), expressed in units of \(e\), is known as a partial charge. It suggests that a fraction of an electron is transferred, although the reality is that there is simply a little more electron density on the more electronegative atom and a little less on the electropositive atom.
How much charge is actually transferred can be quantified by studying the electric dipole moment of the bond, which is a quantity that can be measured experimentally. The electric dipole moment for a diatomic with charges \(Q_1 =Q=\delta e\) and \(Q_2 =-Q =-\delta e\) on atoms 1 and 2, respectively, is
\[\begin{align*}\mu &= Q_1 r_1 +Q_2 r_2\\ &= Qr_1 -Qr_2\\ &=Q(r_1 -r_2)\end{align*}\]
Hence, the magnitude of the dipole moment is
\[\mu = |\mu|=Q|r_1 -r_2|=QR \label{Dipole}\]
where \(R\) is the bond length. As an example, consider \(HF\), which has a partial charge on \(H\) of \(0.41 \;e\), which means \(\delta =0.41\), and a bond length of \(0.926 \ \stackrel{\circ}{A}\). Thus, the magnitude of the dipole moment is
\[|\mu|=0.41(1.602 \times 10^{-19}C)(0.926 \times 10^{-10}m)=6.08\times 10^{-30}C\cdot m\]
Thus, the units of the dipole moment are Coulomb-meters. However, as this example makes clear, this is a very large unit and awkward to work with for molecules. A more convenient unit is the Debye \((D)\), defined to be
\[1\;D=3.336\times 10^{-30}\; \text{Coulomb} \cdot \text{meters}\]
Historically, the Debye was defined in terms of the dipole moment resulting from two equal charges of opposite sign and separated by 1 Ångstrom (\(10^{-10}\; m\)) as 4.801 D from Equation \(\ref{Dipole}\). This value arises from
\[ \dfrac{ (1.602 \times 10^{-19} ) (1 \times 10^{-10}) }{3.336 \times 10^{-30}} \nonumber\]
where
\[D = 3.336 \times 10^{-30}\; C\, m \nonumber\]
or
\[1\; C\, m = 2.9979 \times 10^{29}\; D \nonumber\]
Thus, for a diatomic with partial charges \(+\delta\) and \(-\delta\), the dipole moment in \(D\) is given by
\[\mu (D)=\dfrac{\delta *R(\stackrel{\circ}{A})}{0.2082 \ \stackrel{\circ}{A}D^{-1}}\]
and the percent ionic character is defined in terms of the partial charge \(\delta\) by
\[percent \ ionic \ character=100\% *\delta \label{Ea1}\]
Typical dipole moments for simple diatomic molecules are in the range of 0 to 11 D (Table \(\PageIndex{1}\)). Equation \(\ref{Ea1}\) can be expressed differently in terms of the expected dipole assuming a full charge separation (\( \mu_{ionic}\)) compared to the experimental dipole moment (\( \mu_{exp}\))
\[percent \ ionic \ character=100\% *\dfrac{\mu_{exp}}{\mu_{ionic}} \label{Ea2}\]
Example \(\PageIndex{1}\): KBr
Calculate a theoretical dipole moment for the KBr molecule, assuming opposite charges of one fundamental unit located at each nucleus, and hence the percentage ionic character of KBr.
Solution
From Table \(\PageIndex{1}\), the observed dipole moment of KBr is given as 10.41 D, (3.473 x 10-29 Coulomb-meters), which being close to the upper level of 11 indicates that it is a highly polar molecule. The interatomic distance between K+ and Br- is 282 pm. From this it is possible to calculate a theoretical dipole moment for the KBr molecule, assuming opposite charges of one fundamental unit located at each nucleus, and hence the percentage ionic character of KBr.
Dipole moment
\[μ = q \times e \times d \, (\text{in Coulomb-meters})\]
- q = 1 for complete separation of unit charge
- e = 1.602 x 10-19 C
- d = 2.82 x 10-10 m for KBr (282 pm)
Hence calculated ionic dipole moment is
\[μ_{KBr}= (1) (1.602 \times 10^{-19})( 2.82 \times 10^{-10}) = 4.518 \times 10^{-29}\; Cm = 13.54\; D \nonumber\]
The observed dipole moment is
\[μ_{KBr} = 3.473 \times 10^{-29}\; Cm = 10.41\; D \nonumber\]
the % ionic character from Equation \(\ref{Ea2}\) is
\[KBr = \dfrac{3.473 \times 10^{-29}}{4.518 \times 10^{-29}} \times 100\%= \dfrac{10.41\, D}{13.54\;D} \times 100\% = 76.87\% \nonumber\]
and the % covalent character is therefore about 23% (100% - 77%).
Given the observed dipole moment is 10.41 D (3.473 x 10-29) it is possible to estimate the charge distribution from the same equation by now solving for q.
Dipole moment μ = q * e * d Coulomb metre, but since q is no longer 1 we can substitute in values for μ and d to obtain an estimate for it.
q = μ /(e * d) = 3.473 x 10-29 / (1.602 x 10-19 * 2.82 x 10-10)
thus q = 3.473 x 10-29 / (4.518 x 10-29) = 0.77 and the δ- and δ+ are -0.8 and +0.8 respectively.
Example \(\PageIndex{2}\): NaCl
In the gas phase, NaCl has a dipole moment of 9.001 D and an Na–Cl distance of 236.1 pm. Calculate the percent ionic character in NaCl.
Given: chemical species, dipole moment, and internuclear distance
Asked for: percent ionic character
Strategy:
A Compute the charge on each atom using the information given and Equation 8.4.2.
B Find the percent ionic character from the ratio of the actual charge to the charge of a single electron.
Solution:
A The charge on each atom is given by
\[ Q=\dfrac{\mu }{r} =9.001\;\cancel{D}\left ( \dfrac{3.3356\times 10^{-30}\; C\cdot \cancel{m}}{1\; \cancel{D}} \right )\left ( \dfrac{1}{236.1\; \cancel{pm}} \right )\left ( \dfrac{1\; \cancel{pm}}{10^{-12\;} \cancel{m}} \right )=1.272\times 10^{-19}\;C \]
Thus NaCl behaves as if it had charges of 1.272 × 10−19 C on each atom separated by 236.1 pm.
B The percent ionic character is given by the ratio of the actual charge to the charge of a single electron (the charge expected for the complete transfer of one electron):
\[ \% \; ionic\; character=\left ( \dfrac{1.272\times 10^{-19}\; \cancel{C}}{1.6022\times 10^{-19}\; \cancel{C}} \right )\left ( 100 \right )=79.39\%\simeq 79\% \]
Exercise \(\PageIndex{2}\): AgCl
In the gas phase, silver chloride (AgCl) has a dipole moment of 6.08 D and an Ag–Cl distance of 228.1 pm. What is the percent ionic character in silver chloride?
Answer
55.5%
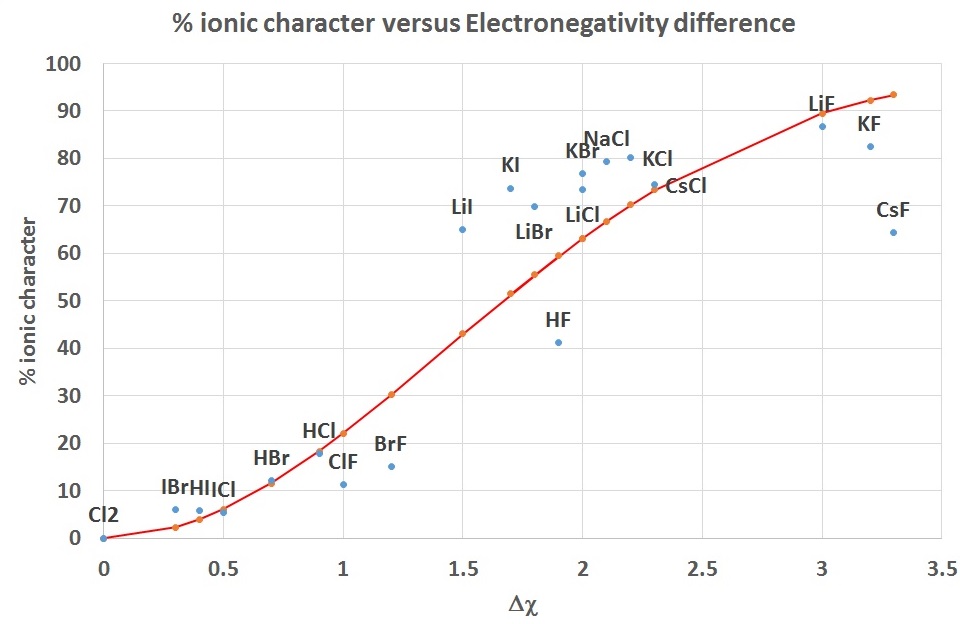
| diatomic | Δ χ | %ionic | bond dist (pm) | \(μ_{exp}\) (D) | \(μ_{ionic}\) (D) |
|---|---|---|---|---|---|
| Cl2 | 0.0 | 0.0 | 200 | 0.00 | 9.60 |
| IBr | 0.3 | 5.9 | 247 | 0.70 | 11.86 |
| HI | 0.4 | 5.7 | 161 | 0.44 | 7.73 |
| ICl | 0.5 | 5.4 | 232 | 0.60 | 11.14 |
| HBr | 0.7 | 12.1 | 141 | 0.82 | 6.77 |
| HCl | 0.9 | 17.7 | 127 | 1.08 | 6.10 |
| ClF | 1.0 | 11.2 | 163 | 0.88 | 7.83 |
| BrF | 1.2 | 15.1 | 178 | 1.29 | 8.55 |
| LiI | 1.5 | 65.0 | 238 | 7.43 | 11.43 |
| HF | 1.9 | 41.2 | 92 | 1.82 | 4.42 |
| LiBr | 1.8 | 69.8 | 217 | 7.27 | 10.42 |
| KI | 1.7 | 73.7 | 305 | 10.80 | 14.65 |
| LiCl | 2.0 | 73.5 | 202 | 7.13 | 9.70 |
| KBr | 2.0 | 76.9 | 282 | 10.41 | 13.54 |
| NaCl | 2.1 | 79.4 | 236 | 9.00 | 11.33 |
| KCl | 2.2 | 80.1 | 267 | 10.27 | 12.82 |
| CsCl | 2.3 | 74.6 | 291 | 10.42 | 13.97 |
| LiF | 3.0 | 86.7 | 152 | 6.33 | 7.30 |
| KF | 3.2 | 82.5 | 217 | 8.60 | 10.42 |
| CsF | 3.3 | 64.4 | 255 | 7.88 | 12.25 |
Pauling proposed an empirical relationship (instead of the defintion in Equation \(\ref{Ea2}\)) which relates the percent ionic character in a bond to the electronegativity difference.
\[percent \ ionic \ character= 100\% \left( 1 - e^{(\Delta χ/2)^2} \right)\]
This is shown as the curve in Figure \(\PageIndex{4}\) and is compared to the values for some diatomic molecules calculated from observed and calculated dipole moments.
As an example, consider \(HF\) again, for which \(\delta = 0.41\). The bond length is \(R=0.926 \ \stackrel{\circ}{A}\). Thus, its dipole moment will be
\[ \mu (D)=\dfrac{0.41*0.926 \stackrel{\circ}{A}}{0.2082 \ \stackrel{\circ}{A}D^{-1}}=1.82D\]
and its percent ionic character is \(41\% \).
Example \(\PageIndex{3}\): Bond Polarity
Without consulting the table of electronegativities (use the periodic table), arrange the following bonds in order of decreasing polarity:
B—Cl, Ba—Cl, Be—Cl, Br—Cl, Cl—Cl.
Solution
We first need to arrange the elements in order of increasing electronegativity. Since the electronegativity increases in going up a column of the periodic table, we have the following relationships:
-
- Ba < Be and Br < Cl
Also since the electronegativity increases across the periodic table, we have
-
- Be < B
Since B is a group III element on the borderline between metals and non-metals, we easily guess that
-
- B < Br
which gives us the complete order
-
- Ba < Be < B < Br < Cl
Among the bonds listed, therefore, the Ba—Cl bond corresponds to the largest difference in electronegativity, i.e., to the most nearly ionic bond. The order of bond polarity is thus
-
- Ba—Cl > Br—Cl > B—Cl > Br—Cl > Cl—Cl
where the final bond, Cl—Cl,is, of course, purely covalent.
Contributors
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)

