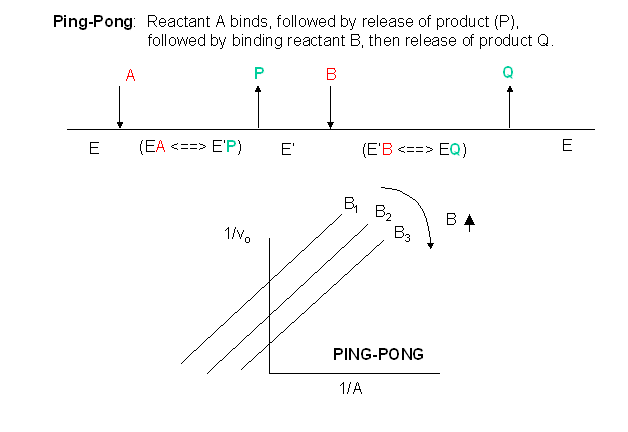10.4: Multisubstrate Systems
- Page ID
- 41364
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Michaelis –Menten model of enzyme kinetics was derived for single substrate reactions. Enzymatic reactions requiring multiple substrates and yielding multiple products are more common and yielding multiple products are more common than single-substrate reaction. In these types of reactions, the all the substrates involved are bound to the enzyme before catalysis of the reaction takes place to release the products. Sequential reactions can be either ordered or random. In contrast to the Michealis-Menton kinetics where a binary Enzyme-Substrate complex is generated in the mechanism (\([ES]\), in bisubstrate enzyme reactions, a ternary complex of the enzyme and two substrates is generated:
\[ A + B \overset{E}{\longrightleftharpoons} P+ Q\]
Bisubstrate reactions account for ~ 60% of the known enzymatic reactions. Multi-substrate reactions follow complex rate equations that describe how the substrates bind and in what sequence. The analysis of these reactions is much simpler if the concentration of substrate \(A\) is kept constant and substrate \(B\) varied. Under these conditions, the enzyme behaves just like a single-substrate enzyme and a plot of \(v\) by \([S]\) gives apparent \(K_M\) and \(V_{max}\) constants for substrate B. If a set of these measurements is performed at different fixed concentrations of A, these data can be used to work out what the mechanism of the reaction is. For an enzyme that takes two substrates A and B and turns them into two products P and Q, there are two types of mechanism: ternary complex and ping–pong.
How do you resolve the enzymes kinetics of these more complicated systems? The answer is fairly straightforward. You keep one of the substrates (B, for example) fixed, and vary the other substrate (A) and obtain a series of hyperbolic plots of \(v_o\) vs \(A\) at different fixed \(B\) concentrations. This would give a series of linear \(1/v\) vs. \(1/A\) double-reciprocal plots (Lineweaver-Burk plots) as well. The pattern of Lineweaver-Burk plots depends on how the reactants and products interact with the enzyme.
Sequential Mechanism
In this mechanism, both substrates must bind to the enzyme before any products are made and released.The substrates might bind to the enzyme in a random fashion (A first then B or vice-versa) or in an ordered fashion (A first followed by B). An abbreviated notation scheme developed by W.W. Cleland is shown in Figure \(\PageIndex{1}\) for the sequential random and sequential ordered mechanisms (Figure \(\PageIndex{1}\)). For both mechanisms, Lineweaver-Burk plots at varying A and different fixed values of B give a series of intersecting lines. Derivative curves can be solved to obtain appropriate kinetic constants. In ordered sequential reactions, all the substrates are first bound to the enzyme in a defined order or sequence. The products, too, are released after catalysis in a defined order or sequence.
An example is the lactate dehydrogenase enzyme, which is a protein that catalyzes glucose metabolism. In this ordered mechanism, the coenzyme, NADH, always binds first, with pyruvate binding afterward. During the reaction, the pyruvate is reduced to lactate while NADH is oxidized to NAD+ by the enzyme. Lactate is then released first, followed by the release of NAD+.

This is a characteristic of a ternary complex, which consists of three molecules that are bound together. Before catalysis, the substrates and coenzyme are bound to the enzyme. After catalysis, the complex consists of the enzyme and products, NAD+ and lactate.
In random sequential reactions, the substrates and products are bound and then released in no preferred order, or "random" order (Figure \(\PageIndex{1}\)). An example is the creatine kinase enzyme, which catalyzes creatine and ATP (the two substrates) to form phosphocreatine and ADP (teh Products) in Figure \(\PageIndex{4}\). In this case, either substrates may bind first and either products may be released first. A ternary complex is still observed for random sequential reactions. Before catalysis, the complex is generated that includes the enzyme, ATP, and creatine. After catalysis, the complex consists of the enzyme, ADP, and phosphocreatine.

Ping-Pong Mechanism
In this mechanism, one substrate bind first to the enzyme followed by product P release. Typically, product P is a fragment of the original substrate A.The rest of the substrate is covalently attached to the enzyme E, which is designated as E'. Now the second reactant, B, binds and reacts with the enzyme to form a covalent adduct with the A as it is covalentattached to the enzyme to form product Q. This is now released and the enzyme is restored to its initial form, E. This represents a ping-pong mechanism. An abbreviated notation scheme is shown below for the ping-pong mechanisms. For this mechanism, Lineweaver-Burk plots at varying A and different fixed values of B give a series of parallel lines. An example of this type of reaction might be low molecular weight protein tyrosine phosphatase against the small substrate p-initrophenylphosphate (A) which binds to the enzyme covalently with the expulsion of the product P, the p-nitrophenol leaving group. Water (B) then comes in and covalently attacks the enzyme, forming an adduct with the covalently bound phosphate releasing it as inorganic phosphate. In this particular example, however, you cannot vary the water concentration and it would be impossible to generate the parallel Lineweaver-Burk plots characteristic of ping-pong kinetics.