2.9: Graham's Laws of Diffusion and Effusion
- Page ID
- 41411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Understand the difference between effusion and diffusion
- To derive and apply Graham's Law of Effusion
Diffusion is the gradual mixing of gases due to the motion of their component particles even in the absence of mechanical agitation such as stirring. The result is a gas mixture with uniform composition. Diffusion is also a property of the particles in liquids and liquid solutions and, to a lesser extent, of solids and solid solutions. The related process, effusion, is the escape of gaseous molecules through a small (usually microscopic) hole, such as a hole in a balloon, into an evacuated space.
The phenomenon of effusion had been known for thousands of years, but it was not until the early 19th century that quantitative experiments related the rate of effusion to molecular properties. The rate of effusion of a gaseous substance is inversely proportional to the square root of its molar mass. This relationship is referred to as Graham’s law, after the Scottish chemist Thomas Graham (1805–1869). The ratio of the effusion rates of two gases is the square root of the inverse ratio of their molar masses:
\[ \color{red} \dfrac{\text{rate of effusion A}}{\text{rate of effusion B}}=\sqrt{\dfrac{M_B}{M_A}} \label{1}\]
Graham Law
The rate of effusion of a gaseous substance is inversely proportional to the square root of its molar mass.
Graham’s law is an empirical relationship that states that the ratio of the rates of diffusion or effusion of two gases is the square root of the inverse ratio of their molar masses. The relationship is based on the postulate that all gases at the same temperature have the same average kinetic energy (recall that a result of the Kinetic Theory of Gases is that the temperature, in degrees Kelvin, is directly proportional to the average kinetic energy of the molecules.) . We can write the expression for the average kinetic energy of two gases with different molar masses:
\[KE=\dfrac{1}{2}\dfrac{M_{\rm A}}{N_A}v_{\rm rms,A}^2=\dfrac{1}{2}\dfrac{M_{\rm B}}{N_A}v_{\rm rms,B}^2\label{2}\]
Multiplying both sides by 2 and rearranging give
\[\dfrac{v_{\rm rms, B}^2}{v_{\rm rms,A}^2}=\dfrac{M_{\rm A}}{M_{\rm B}}\label{3}\]
Taking the square root of both sides gives
\[\dfrac{v_{\rm rms, B}}{v_{\rm rms,A}}=\sqrt{\dfrac{M_{\rm A}}{M_{\rm B}}}\label{4}\]
Thus the rate at which a molecule, or a mole of molecules, diffuses or effuses is directly related to the speed at which it moves. Equation \(\ref{4}\) shows that Graham’s law is a direct consequence of the fact that gaseous molecules at the same temperature have the same average kinetic energy.
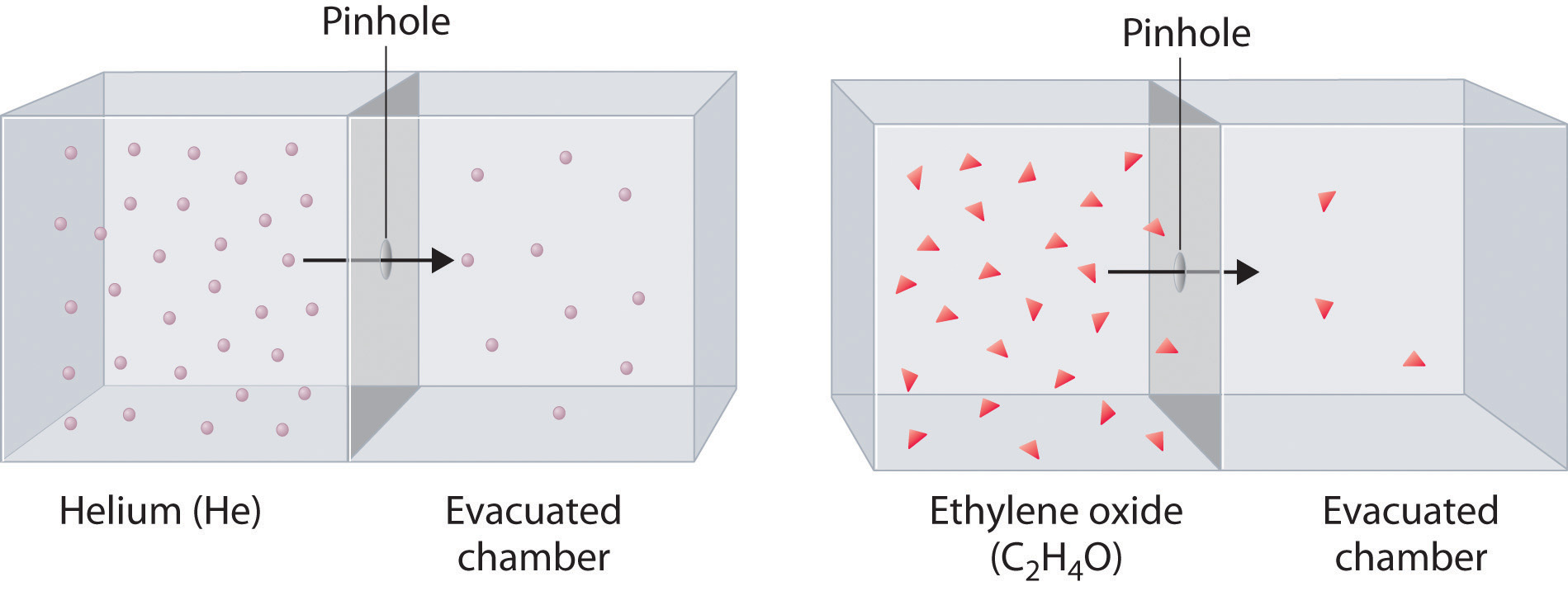
Heavy molecules effuse through a porous material more slowly than light molecules, as illustrated schematically in Figure \(\PageIndex{1}\) for ethylene oxide \(C_2H_4O \) and helium \(He\). Helium (M = 4.00 g/mol) effuses much more rapidly than ethylene oxide (M = 44.0 g/mol). Because helium is less dense than air, helium-filled balloons “float” at the end of a tethering string. Unfortunately, rubber balloons filled with helium soon lose their buoyancy along with much of their volume. In contrast, rubber balloons filled with air tend to retain their shape and volume for a much longer time. Because helium has a molar mass of 4.00 g/mol, whereas air has an average molar mass of about 29 g/mol, pure helium effuses through the microscopic pores in the rubber balloon \(\sqrt{\frac{29}{4.00}}=2.7\) times faster than air. For this reason, high-quality helium-filled balloons are usually made of Mylar, a dense, strong, opaque material with a high molecular mass that forms films that have many fewer pores than rubber. Hence, mylar balloons can retain their helium for days.
Example \(\PageIndex{1}\)
During World War II, scientists working on the first atomic bomb were faced with the challenge of finding a way to obtain large amounts of \(\ce{^{235}U}\). Naturally occurring uranium is only 0.720% \(\ce{^{235}U}\), whereas most of the rest (99.275%) is \(\ce{^{238}U}\), which is not fissionable (i.e., it will not break apart to release nuclear energy) and also actually poisons the fission process. Because both isotopes of uranium have the same reactivity, they cannot be separated chemically. Instead, a process of gaseous effusion was developed using the volatile compound \(UF_6\) (boiling point = 56°C).
- Calculate the ratio of the rates of effusion of 235UF6 and 238UF6 for a single step in which UF6 is allowed to pass through a porous barrier. (The atomic mass of 235U is 235.04, and the atomic mass of 238U is 238.05.)
- If n identical successive separation steps are used, the overall separation is given by the separation in a single step (in this case, the ratio of effusion rates) raised to the nth power. How many effusion steps are needed to obtain 99.0% pure 235UF6?
Given: isotopic content of naturally occurring uranium and atomic masses of 235U and 238U
Asked for: ratio of rates of effusion and number of effusion steps needed to obtain 99.0% pure 235UF6
Strategy:
- Calculate the molar masses of 235UF6 and 238UF6, and then use Graham’s law to determine the ratio of the effusion rates. Use this value to determine the isotopic content of 235UF6 after a single effusion step.
- Divide the final purity by the initial purity to obtain a value for the number of separation steps needed to achieve the desired purity. Use a logarithmic expression to compute the number of separation steps required.
Solution:
- A The first step is to calculate the molar mass of UF6 containing 235U and 238U. Luckily for the success of the separation method, fluorine consists of a single isotope of atomic mass 18.998. The molar mass of 235UF6 is
234.04 + (6)(18.998) = 349.03 g/mol
The molar mass of 238UF6 is
238.05 + (6)(18.998) = 352.04 g/molThe difference is only 3.01 g/mol (less than 1%). The ratio of the effusion rates can be calculated from Graham’s law using Equation \(\ref{1}\):
\[\rm\dfrac{\text{rate }^{235}UF_6}{\text{rate }^{238}UF_6}=\sqrt{\dfrac{352.04\;g/mol}{349.03\;g/mol}}=1.0043\] -
rate U235F6rate U238F6=352.04349.03−−−−−−√=1.0043
Thus passing UF6 containing a mixture of the two isotopes through a single porous barrier gives an enrichment of 1.0043, so after one step the isotopic content is (0.720%)(1.0043) = 0.723% 235UF6.
- B To obtain 99.0% pure 235UF6 requires many steps. We can set up an equation that relates the initial and final purity to the number of times the separation process is repeated:
final purity = (initial purity)(separation)n
In this case, 0.990 = (0.00720)(1.0043)n, which can be rearranged to give
\[1.0043^n=\dfrac{0.990}{0.00720}=137.50\] - Taking the logarithm of both sides gives
\[n\ln(1.0043)=\ln(137.50)\]
\[n=\dfrac{\ln(137.50)}{\ln(1.0043)}=1148\]Thus at least a thousand effusion steps are necessary to obtain highly enriched 235U. Figure \(\PageIndex{2}\) shows a small part of a system that is used to prepare enriched uranium on a large scale.

Exercise \(\PageIndex{1}\)
Helium consists of two isotopes: 3He (natural abundance = 0.000134%) and 4He (natural abundance = 99.999866%). Their atomic masses are 3.01603 and 4.00260, respectively. Helium-3 has unique physical properties and is used in the study of ultralow temperatures. It is separated from the more abundant 4He by a process of gaseous effusion.
- Calculate the ratio of the effusion rates of 3He and 4He and thus the enrichment possible in a single effusion step.
- How many effusion steps are necessary to yield 99.0% pure 3He?
Answer: a. ratio of effusion rates = 1.15200; one step gives 0.000154% 3He; b. 96 steps
Gas molecules do not diffuse nearly as rapidly as their very high speeds might suggest. If molecules actually moved through a room at hundreds of miles per hour, we would detect odors faster than we hear sound. Instead, it can take several minutes for us to detect an aroma because molecules are traveling in a medium with other gas molecules. Because gas molecules collide as often as 1010 times per second, changing direction and speed with each collision, they do not diffuse across a room in a straight line.
Summary
Gaseous particles are in constant random motion. Gaseous particles tend to undergo diffusion because they have kinetic energy. Diffusion is faster at higher temperatures because the gas molecules have greater kinetic energy. Effusion refers to the movement of gas particles through a small hole. Graham's Law states that the effusion rate of a gas is inversely proportional to the square root of the mass of its particles.

