10.7: Benzene and Aromaticity
- Page ID
- 53694
- Apply Hückel theory to describing the pi bonding in cyclical conjugated system
- Identify the origin of aromaticity within Hückel theory to describe extra stabilization in certain cyclical conjugated systems
The previous sections addressed the \(\pi\) orbitals of linear conjugated system. Here we address conjugated systems of cyclic conjugated hydrocarbons with the general formula of \(C_nH_n\) where \(n\) is the number of carbon atoms in the ring. The molecule from this important class of organic molecule that you are most familiar with is benzene (\(C_6H_6\)) with \(n=6\), although many other molecules exist like cyclobutadiene (\(C_4H_4\)) with \(n=4\) (Figure 10.7.1 ).
The structure of benzene is an interesting historical topic. In 1865, the German chemist Friedrich August Kekulé published a paper suggesting that the structure of benzene contained a ring of six carbon atoms with alternating single and double bonds. Within this argument, two resonance structures can be formulated.
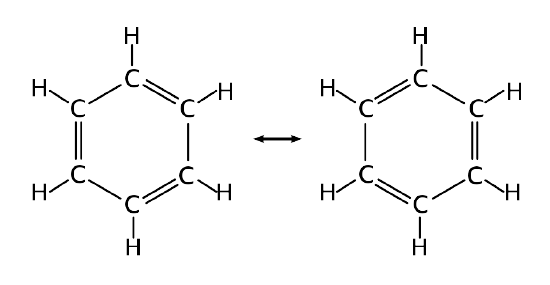
However, X-ray diffraction shows that all six carbon-carbon bonds in benzene are of the same length, at 140 pm. The C–C bond lengths are greater than a double bond (135 pm), but shorter than a typical single bond (147 pm). This means that neither structures Figure 10.7.2 are correct and the true 'structure' of benzene is a mixture of the two. As discussed previously, that such a valence bond perspective results in a delocalization energy within a molecular orbital approach.
Aromatic systems provide the most significant applications of Hückel theory. For benzene, we find the secular determinant
\[\left|\begin{array}{cccccc}x&1&0&0&0&1\\1&x&1&0&0&0\\0&1&x&1&0&0\\0&0&1&x&1&0\\0&0&0&1&x&1\\1&0&0&0&1&x\end{array}\right|=0\label{31} \]
with the six roots \(x=\pm2,\pm1,\pm1\). This corresponds to the following energies (ordered from most stable to least since \(\beta < 0\)):
- \(E_1 = α + 2β\)
- \(E_2 = α + β\)
- \(E_3 = α + β\)
- \(E_4 = α − β\)
- \(E_5 = α − β\)
- \(E_6 = α − 2β\)
The two pairs of \(E=\alpha\pm\beta\) energy levels are two-fold degenerate (Figure 10.7.3 ).
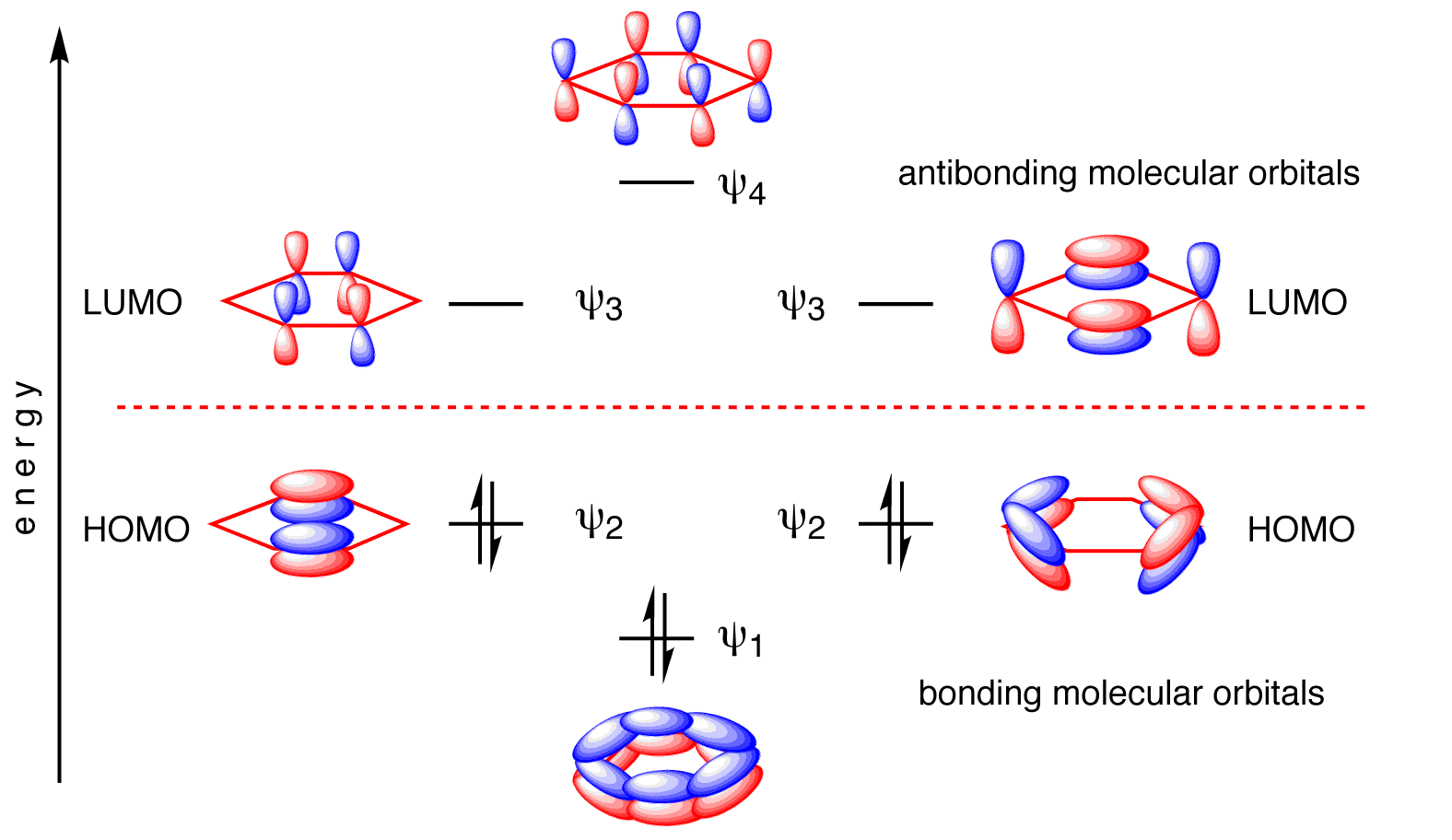
The resulting wavefunctions are below (expanded in terms of carbon \(| 2p\rangle\) atomic orbitals).
\[ \begin{align} | \psi_1 \rangle &= \dfrac{1}{\sqrt{6}} \left[ | 2p_{z1} \rangle+ | 2p_{z2} \rangle + | 2p_{z3} \rangle + | 2p_{z4} \rangle + | 2p_{z5} \rangle + | 2p_{z6} \rangle \right] \\ | \psi_2 \rangle &= \dfrac{1}{\sqrt{4}} \left[ | 2p_{z2} \rangle + | 2p_{z3} \rangle - | 2p_{z4} \rangle - | 2p_{z5} \rangle \right] \\ | \psi_3 \rangle &= \dfrac{1}{\sqrt{3}} \left[ | 2p_{z1} \rangle + \dfrac{1}{2}| 2p_{z2} \rangle - \dfrac{1}{2} | 2p_{z3} \rangle - | 2p_{z4} \rangle - \dfrac{1}{2} | 2p_{z5} \rangle + \dfrac{1}{2} | 2p_{z6} \rangle \right] \\ | \psi_4 \rangle &= \dfrac{1}{\sqrt{4}} \left[ | 2p_{z2} \rangle - | 2p_{z3} \rangle + | 2p_{z4} \rangle - | 2p_{z5} \rangle \right] \\ | \psi_5 \rangle &= \dfrac{1}{\sqrt{3}} \left[ | 2p_{z1} \rangle - \dfrac{1}{2}| 2p_{z2} \rangle - \dfrac{1}{2} | 2p_{z3} \rangle + | 2p_{z4} \rangle - \dfrac{1}{2} | 2p_{z5} \rangle - \dfrac{1}{2} | 2p_{z6} \rangle \right] \\ | \psi_6 \rangle &= \dfrac{1}{\sqrt{6}} \left[ | 2p_{z1} \rangle- | 2p_{z2} \rangle + | 2p_{z3} \rangle - | 2p_{z4} \rangle + | 2p_{z5} \rangle - | 2p_{z6} \rangle \right] \end{align} \nonumber \]
Each of the carbons in benzene contributes one electron to the \(\pi\)-bonding framework (Figure 10.7.3 ). This means that all bonding molecular orbitals are fully occupied and benzene then has an electron configuration of \(\pi_1^2 \pi_2^2 \pi_3^2 \). With the three lowest molecular orbitals occupied, the total \(\pi\)-bonding energy is
\[E_{tot} (benzene)=2(\alpha+2\beta)+4(\alpha+\beta)=6\alpha+8\beta\label{32} \]
Since the energy of a localized double bond is \( 2(\alpha+\beta)\), as determined from the analysis of ethylene, the delocalization energy of benzene is
\[ \Delta E = E_{tot} (benzene) - 3 E_{tot} (ethylene) = (6\alpha+8\beta ) - 3 \times 2(\alpha+\beta) = 2\beta \nonumber \]
The experimental thermochemical value is -152 kJ mol-1.
Aromaticity
In general, cyclic polyenes are only closed shell (i.e., each electron paired up) and extra stable for with (4n+2) \(\pi\) electrons (n=0,1,2…). These special molecules have the highest delocalization energies and are said to be “aromatic”. For benzene this is \( 2\beta\) (Equation \(\ref{32}\)), which is the energy by which the delocalized \(\pi\) electrons in benzene are more stable than those in three isolated double bonds.
A stable, closed-shell conjugated cyclic structure is obtained for molecules with (4n+ 2) electrons with n=2, 6, 10, .... electrons.
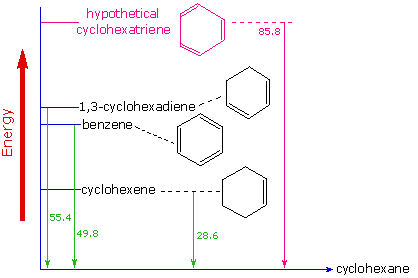
Evidence for the enhanced thermodynamic stability of benzene was obtained from measurements of the heat released when double bonds in a six-carbon ring are hydrogenated (hydrogen is added catalytically) to give cyclohexane as a common product. In the following diagram cyclohexane represents a low-energy reference point. Addition of hydrogen to cyclohexene produces cyclohexane and releases heat amounting to 11.9 kJ mol-1. If we take this value to represent the energy cost of introducing one double bond into a six-carbon ring, we would expect a cyclohexadiene to release 23.9 kJ mol-1 on complete hydrogenation, and 1,3,5-cyclohexatriene to release 35.9 kJ mol-1. These heats of hydrogenation \(\Delta H_{hyd}\) reflect the relative thermodynamic stability of the compounds (Figure 10.7.4 ). In practice, 1,3-cyclohexadiene is slightly more stable than expected, by about 8.1 kJ mol-1, presumably due to conjugation of the double bonds. Benzene, however, is an extraordinary 15 kJ mol-1 more stable than expected. This additonal stability is a characteristic of all aromatic compounds.
Contributors and Attributions
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
- Wikipedia

