8.7: Hartree-Fock Calculations Give Good Agreement with Experimental Data
- Page ID
- 13445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Understand how the Hartree method is expanded to include symmetrized mulit-electron determential wavefunctions via the Hartree-Fock equations.
- Understand how to calculate the orbital energies from HF theory.
- Apply HF theory with Koopman's theory to estimate ionization energies and electron affinities.
The Hartree method discussed previously is useful as an introduction to the solution of many-particle system and to the concepts of self-consistency and of the self-consistent-field calculations, but its importance is confined to the history of physics. In fact the Hartree method is not just approximate, it is fundamentally wrong since its wavefunction is not antisymmetric to electron permutation! The Hartree-Fock approach discussed below is a better approach, which correctly takes into account the antisymmetric character of the trial wavefunctions.
Although the Hartree equations are numerically tractable via the self-consistent field method, it is not surprising that such a crude approximation fails to capture elements of the essential physics. The Pauli exclusion principle demands that the many-body wavefunction be antisymmetric with respect to interchange of any two electron coordinates, e.g.
\[\Psi(\mathbf{r}_{1},\mathbf{r}_{2}, \ldots, \mathbf{r}_{N}) = - \Psi(\mathbf{r}_{2},\mathbf{r}_{1}, \ldots, \mathbf{r}_{N}) \label{2.7} \]
which clearly cannot be satisfied by the multi-electron wavefunctions of the form used in the Hartree Approximation, i.e., the orbital approximation (Equation \(\ref{2.3}\)).
\[\Psi(\mathbf{r}_1,\mathbf{r}_2, \ldots, \mathbf{r}_N) \approx \psi_{1}(\mathbf{r}_1)\psi_{2}(\mathbf{r}_2) \ldots \psi_{N}(\mathbf{r}_N) \label{2.3} \]
This indistinguishability condition can be satisfied by forming a Slater determinant of single-particle orbitals
\[\Psi(\mathbf{r}_{1}, \mathbf{r}_{2}, \ldots, \mathbf{r}_{N})= \dfrac{1}{\sqrt{N}} \left \vert\psi(\mathbf{r}_{1})\psi(\mathbf{r}_{2}) \ldots \psi(\mathbf{r}_{N}) \right\vert \label{2.8} \]
This decouples the electrons resulting in \(N\) single-particle Hartree-Fock equations:
\[\underbrace{-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r})}_{\text{kinetic energy}} + \underbrace{V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{electron-nucleus potential}} + \underbrace{V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r})}_{\text{Hartree Term}} - \sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} = \epsilon_{i}\psi_{i}(\mathbf{r}). \label{2.9} \]
As with the Hartree equations, the first term is the kinetic energy of the \(i^{th}\) electron
\[-\dfrac{\hbar^{2}}{2m}\nabla^{2}\psi_{i}(\mathbf{r}) \nonumber \]
and the second term is the electron-nucleus potential between the \(i^{th}\) electron and nucleus
\[V_{nucleus}(\mathbf{r})\psi_{i}(\mathbf{r}) \nonumber \]
The third term (sometimes called the “Hartree” term) is the electrostatic potential between the \(i^{th}\) electron and the average charge distribution of the other \(N-1\) electrons.
\[V_{electron}(\mathbf{r})\psi_{i}(\mathbf{r}) = J_{j,k} = \int |\phi_j(r)|^2 |\phi_k(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{8.3.9} \]
These three terms are identical to Hartree Equations with the product wavefunction ansatz (i.e., orbital approximation). The fourth term of Equation \(\ref{2.9}\) is not in the Hartree Equations:
\[\sum_{j} \int d\mathbf{r}^{\prime} \dfrac{\psi^{\star}_{j}(\mathbf{r}') \psi^{\star}_{i}(\mathbf{r}') \psi_{j}(\mathbf{r}) } {\left \vert \mathbf{r} - \mathbf{r}^{\prime} \right\vert} \nonumber \]
and is the exchange term. This term resembles the direct Coulomb term, but for the exchanged indices. It is a manifestation of the Pauli exclusion principle, and acts so as to separate electrons of the same spin. This “exchange” term acts only on electrons with the same spin and comes from the Slater determinant form of the wavefunction (Equation \ref{2.8}). Physically, the effect of exchange is for like-spin electrons to avoid each other. The exchange term adds considerably to the complexity of these equations.
The Hartree-Fock Equations in Equation \(\ref{2.9}\) can be recast as series of Schrödinger-like equations:
\[ \hat {F} | \varphi _i \rangle = \epsilon _i| \varphi _i \rangle \label {8.7.2} \]
where \(\hat {F}\) is called the Fock operator and \( \{| \varphi_i \rangle \}\) are the Hatree-Fock orbitals with corresponding energies \(\epsilon_i\).
The Fock operator is a one-electron operator and solving a Hartree-Fock equation gives the energy and Hartree-Fock orbital for one electron. For a system with 2N electrons, the variable i will range from 1 to N; i.e there will be one equation for each orbital. The reason for this is that only the spatial wavefunctions are used in Equation \(\ref{8.7.2}\). Since the spatial portion of an orbital can be used to describe two electrons, each of the energies and wavefunctions found by solving Equation \(\ref{8.7.2}\) will be used to describe two electrons.
The nature of the Fock operator reveals how the Hartree-Fock (HF) or Self-Consistent Field (SCF) Method accounts for the electron-electron interaction in atoms and molecules while preserving the idea of independent atomic orbitals. The wavefunction written as a Slater determinant of spin-orbitals is necessary to derive the form of the Fock operator, which is
\[\begin{align} \hat {F} &= \hat {H} ^0 + \sum _{j=1}^N ( 2 \hat {J} _j - \hat {K} _j ) \nonumber \\[4pt] &= -\dfrac {\hbar ^2}{2m} \nabla ^2 - \dfrac {Ze^2}{4 \pi \epsilon _0 r} + \sum _{j=1}^N (2\hat {J}_j - \hat {K} _j ) \label {8.7.3} \end{align}\]
As shown by the expanded version on the far right, the first term in this equation, \(\hat {H}^0\), is the familiar hydrogen-like operator that accounts for the kinetic energy of an electron and the potential energy of this electron interacting with the nucleus. The next term accounts for the potential energy of one electron in an average field created by all the other electrons in the system. The \(\hat {J}\) and \(\hat {K}\) operators result from the electron-electron repulsion terms in the full Hamiltonian for a multi-electron system. These operators involve the one-electron orbitals as well as the electron-electron interaction energy.
The Fock operator (Equation \(\ref{8.7.3}\)) depends on all occupied orbitals (because of the exchange and Coulomb operators). Therefore, a specific orbital can only be determined if all the others are known. One must use iterative methods to solve the HF equations like the Self-consistent field method discussed previously for the Hartree Approximation.
The exchange interaction is a quantum mechanical effect that only occurs between identical particles. Despite sometimes being called an exchange force in analogy to classical force, it is not a true force, as it lacks a force carrier. The effect is due to the wavefunction of indistinguishable particles being subject to exchange symmetry, that is, either remaining unchanged (symmetric) or changing its sign (antisymmetric) when two particles are exchanged. Both bosons and fermions can experience the exchange interaction. For fermions, it is sometimes called Pauli repulsion and related to the Pauli exclusion principle. For bosons, the exchange interaction takes the form of an effective attraction that causes identical particles to be found closer together, as in Bose–Einstein condensation.
For example, the electron 1 in helium (with \(Z=2\)), then
\[\hat {H}^0 (1) = - \dfrac {\hbar ^2}{2m} \nabla ^2_1 - \dfrac {2e^2}{4 \pi \epsilon _0 r_1} \nonumber \]
The Fock operator is couched in terms of the coordinates of the one electron whose perspective we are taking (which we will call electron 1 throughout the following discussion), and the average field created by all the other electrons in the system is built in terms of the coordinates of a generic “other electron” (which we’ll call electron 2) that is considered to occupy each orbital in turn during the summation over the \(N\) spatial orbitals. The best possible one-electron wavefunctions, by definition, will give the lowest possible total energy for a multi-electron system used with the complete multielectron Hamiltonian to calculate the expectation value for the total energy of the system. These wavefunctions are called the Hartree-Fock wavefunctions and the calculated total energy is the Hartree-Fock energy of the system.
As with the Hartree Equations, solving the Hartree-Fock Equations is mathematically equivalent to assuming each electron interacts only with the average charge cloud of the other electrons. This is how the electron-electron repulsion is handled. This also why this approach is also called the Self-Consistant Field (SCF) approach.
Hartree-Fock Energy
The Hartree-Fock equations \(h_e \phi_i = \epsilon_i \phi_i\) imply that the orbital energies \(\epsilon_i\) can be written as:
\[ \begin{align*} \epsilon_i &= \langle \phi_i | h_e | \phi_i \rangle \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} \langle \phi_i | J_j - K_j | \phi_i \rangle \label{8.7.6} \\[4pt] &= \langle \phi_i | T + V | \phi_i \rangle + \sum_{j({\rm occupied})} [ J_{i,j} - K_{i,j} ],\label{8.7.7} \end{align*} \]
where \(T + V\) represents the kinetic (\(T\)) and nuclear attraction (\(V\)) energies, respectively. Thus, \(\epsilon_i\) is the average value of the kinetic energy plus Coulombic attraction to the nuclei for an electron in \(\phi_i\) plus the sum over all of the spin-orbitals occupied in \(\psi\) of Coulomb minus Exchange interactions of these electrons with the electron in \(\phi_i\).
If \(\phi_i\) is an occupied spin-orbital, the \(j = i\) term \([ J_{i,i} - K_{i,i}]\) disappears in the above sum and the remaining terms in the sum represent the Coulomb minus exchange interaction of \(\phi_i\) with all of the \(N-1\) other occupied spin-orbitals. If \(\phi_i\) is a virtual spin-orbital, this cancelation does not occur because the sum over \(j\) does not include \(j = i\). So, one obtains the Coulomb minus exchange interaction of \(\phi_i\) with all \(N\) of the occupied spin-orbitals in \(\psi\). Hence the energies of occupied orbitals pertain to interactions appropriate to a total of \(N\) electrons, while the energies of virtual orbitals pertain to a system with \(N+1\) electrons. This difference is very important to understand and to keep in mind.
To give an idea of how well HF theory can predict the ground state energies of several atoms, consider Table 8.7.1 below:
| Atom | Hartree-Fock Energy | Experiment |
|---|---|---|
| \(He\) | \(-5.72\) | \(-5.80\) |
| \(Li\) | \(-14.86\) | \(-14.96\) |
| \(Ne\) | \(-257.10\) | \(-257.88\) |
| \(Ar\) | \(-1053.64\) | \(-1055.20\) |
Koopmans' Theorem
Koopmans' theorem states that the first ionization energy is equal to the negative of the orbital energy of the highest occupied molecular orbital. Hence, the ionization energy required to generated a cation and detached electron is represented by the removal of an electron from an orbital without changing the wavefunctions of the other electrons. This is called the "frozen orbital approximation." Let us consider the following model of the detachment or attachment of an electron in an \(N\)-electron system.
- In this model, both the parent molecule and the species generated by adding or removing an electron are treated at the single-determinant level.
- The Hartree-Fock orbitals of the parent molecule are used to describe both species. It is said that such a model neglects orbital relaxation (i.e., the re-optimization of the spin-orbitals to allow them to become appropriate to the daughter species).
Within this model, the energy difference between the daughter and the parent can be written as follows (\(\phi_k\) represents the particular spin-orbital that is added or removed:
- for electron detachment (vertical ionization energies) \[ E_{N-1} - E_N = - \epsilon_k \label{8.7.8} \]
- and for electron attachment (electron affinities) \[ E_N - E_{N+1} = - \epsilon_k .\label{8.7.9} \]
The Hartree-Fock equations deal with exchange exactly; however, the equations neglect more detailed correlations due to many-body interactions. The effects of electronic correlations are not negligible; indeed the failure of Hartree-Fock theory to successfully incorporate correlation leads to one of its most celebrated failures.
Let’s derive this result for the case in which an electron is added to the \(N+1^{st}\) spin-orbital. The energy of the \(N\)-electron determinant with spin-orbitals \(\phi_1\) through \(f_N\) occupied is
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \sum_{i=1}^{N} [ J_{i,j} - K_{i,j} ] \nonumber \]
which can also be written as
\[E_N = \sum_{i=1}^N \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N} [ J_{i,j} - K_{i,j} ].\nonumber \]
Likewise, the energy of the \(N+1\)-electron determinant wavefunction is
\[E_{N+1} = \sum_{i=1}^{N+1} \langle \phi_i | T + V | \phi_i \rangle + \frac{1}{2} \sum_{i,j=1}^{N+1} [ J_{i,j} - K_{i,j} ]. \nonumber \]
The difference between these two energies is given by
\[ \begin{align*} E_{N} – E_{N+1} = &- \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \frac{1}{2} \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &- \frac{1}{2} \sum_{j=1}^{N+1} [ J_{N+1,j} - K_{N+1,j} ] \\[4pt] &= - \langle \phi_{N+1} | T + V | \phi_{N+1} \rangle - \sum_{i=1}^{N+1} [ J_{i,N+1} - K_{i,N+1} ] \\[4pt] &= - \epsilon_{N+1}. \end{align*} \nonumber \]
That is, the energy difference is equal to minus the expression for the energy of the \(N+1^{st}\) spin-orbital, which was given earlier.
In the Copenhagen Interpretation, the squared modulus of the wavefunction gives the probability of finding a particle in a given place. The many-body wavefunction gives the N-particle distribution function, i.e. \(|Φ(r_1, ..., r_N )|^2\) is the probability density that particle 1 is at \(r_1\), ..., and particle \(N\) is at \(r_N\). However, when trying to work out the interaction between electrons, what we want to know is the probability of finding an electron at \(r\), given the positions of all the other electrons \(\{r_i\}\). This implies that the electron behaves quantum mechanically when we evaluate its wavefunction, but as a classical point particle when it contributes to the potential seen by the other electrons.
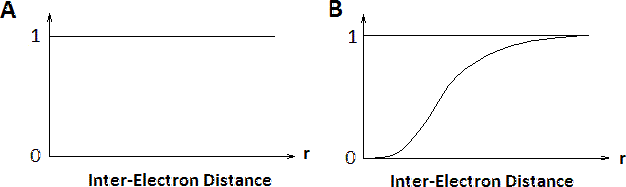
The contributions of electron-electron interactions in N-electron systems within the Hartree and Hartree-Fock methods are shown in Figure 8.7.2 . The conditional electron probability distributions \(n(r)\) of \(N-1\) electrons around an electron with given spin situated at \(r=0\). Within the Hartree approximation, all electrons are treated as independent, therefore \(n(r)\) is structureless. However, within the Hartree-Fock approximation, the \(N\)-electron wavefunction reflects the Pauli exclusion principle and near the electron at \(r=0\) the exchange hole can be seen where the the density of spins equal to that of the central electron is reduced. Electrons with opposite spins are unaffected (not shown).
Summary
So, within the limitations of the HF, frozen-orbital model, the ionization potentials (IPs) and electron affinities (EAs) are given as the negative of the occupied and virtual spin-orbital energies, respectively. This statement is referred to as Koopmans’ theorem; it is used extensively in quantum chemical calculations as a means of estimating ionization potentials (Equation \(\ref{8.7.8}\)) and Electron Affinities (Equation \(\ref{8.7.9}\)) and often yields results that are qualitatively correct (i.e., ± 0.5 eV). In general Hartree-Fock theory gives a great first order solution (99%) to describing multi-electron systems, but that last 1% is still too great for quantitatively describing many aspects of chemistry and more sophisticated approaches are necessary. These are discussed elsewhere.


