Fluorescence Lifetimes and Dynamic Quenching

Learning Objectives

• Goal: Fluorescent lifetime data are presented for two aqueous systems that contain varying amounts of a quenching agent. A Stern-Volmer analysis is carried out on each data set and the bimolecular quenching rate constant is determined for each system.
• Prerequisites: An introductory understanding of spectroscopic and kinetic principles, including general and integrated rate laws.
• Resources you will need: This exercise should be carried out within a software environment that is capable of data manipulation and which can generate a best-fit line for an x-y data set. You will also be graphing the data along with the fitted function.

When an atom or molecule is electronically excited by the absorption of a photon, there are a number of schemes by which that species can then return to the ground state. One mode involves the emission of a photon of light, which causes the substance to fluoresce or phosphorese. Alternatively, species can lose their excitation by nonradiative means:

1. through collisions with other atoms or molecules or
2. by simply returning to the ground state along a down-hill energy path that involves several coupled vibrational and electronic energy states.

The first of these nonradiative schemes is called dynamic quenching, and will be our primary focus in the exercise below.

Fluorescence or phosphorescence lifetime measurements are often used to investigate the various modes of de-excitation that occur following photo-excitation. In such an experiment, a pulsed laser or gas discharge lamp is used to excite a small population of excited state atoms or molecules. In solution, the lifetimes of excited states can be extremely short (on the order of nanoseconds). Therefore, the light source that is employed in solution studies must emit pulses that are generally 1 ns or shorter.

Let us assume that we fire the laser once and generate a temporary concentration of excited state molecules \([A^*]\) at some moment in time. Let us further assume that \(A^*\) is strongly fluorescent, and that we can follow the intensity of this fluorescence at later times using a sensitive light detector like a photomultiplier tube. How do we expect the fluorescence to decay in time? Will it decay linearly, in an exponential fashion, or some other way? And what will the shape of this decay curve tell us about the various de-excitation schemes that are occurring in the system?

If there are no quenching agents present in our system (i.e. there are no species in solution that can effectively quench the fluorescence through bimolecular collisions), then A* can return to the ground state by simple fluorescence

\[A^* \ce{ ->[k_1]} A + h\nu \label{1}\]

and by non-radiative decay

\[A^* \ce{ ->[k_2]} A \label{2}\]

where \(k_1\) and \(k_2\) are the rate constants for these two processes. With only these two paths to the ground state available, the rate equation for \([A^*]\) can be written as

\[ \dfrac{[A^*]}{dt} = - k_1 [A^*] - k_2 [A^*] = -( k_1 + k_2)[A^*] \label{3}\]

Rearrangment and integration of Equation \ref{3} with respect to initial conditions \(t = 0\) and \([A^*] = [A^*]_0\) gives

\[ [A^*] = [A^*]_0 e^{-(k_1+k_2)/t}. \label{4}\]

According to this result, the concentration of excited species (and the fluorescence) is expected to decay away in an exponential fashion. The rate constants \(k_1\) and \(k_2\) quantify how quickly the fluorescence decays. For convenience, we will define a ‘fluorescence lifetime in the absence of quencher’

\[ \tau_o = \dfrac{1}{k_1+k_2} \label{5}\]

\(\tau_o\) is the amount of time that it take for the fluorescence intensity to decay to \(1/e\) its initial value. A typical fluorescence decay curve is shown below in Figure \(\PageIndex{1}\) (the time axis is in units of nanoseconds). The fluorescence intensity spikes upward when the sample is irradiated by the light pulse (at 10 ns), and the intensity decays away in an exponential fashion (the lifetime associated with this particular curve is approximately 30 ns).

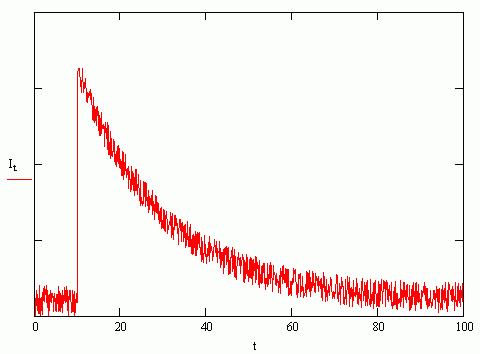
Figure \(\PageIndex{1}\)

If a quenching agent (\(Q\)) is present in solution, then a third process becomes available for returning \(A^*\) molecules to the ground state;

\[A^* +Q \ce{ ->[k_q]} A \label{6}\]

and the rate equation (Equation \ref{3}) for \([A^*]\) then becomes

\[ \dfrac{[A^*]}{dt} = -( k_1 + k_2 + k_q[Q])[A^*] \label{7}\]

\(k_q\) which appears in Equations \ref{6} and \ref{7} is called the bimolecular quenching constant. Assuming \([Q] \gg [A^*]\), which means \([Q]\) can be treated as a constant (the concentration of quencher is normally orders of magnitude larger than \(A^*\) in practice), then Equation \ref{7} can be integrated to give

\[ [A^*] = [A^*]_0 e^{-(k_1+k_2+k_q[Q])/t}. \label{8}\]

Consequently, the fluorescence decay is still exponential, but the fluorescence lifetime (with quencher) becomes

\[ \tau_o = \dfrac{1}{k_1+k_2+k_q[Q]} \label{9}\]

To isolate the effects of quenching, fluorescence lifetime measurements are carried out over a range of quenching agent concentrations (including \([Q] = 0\)). A fluorescence decay curve is recorded for each trial and each decay curve is fit to an exponential function, which yields a lifetime for each trial. Dividing Equation \ref{9} into Equation \ref{5} gives

\[ \begin{align} \dfrac{\tau_o}{\tau} &= \dfrac{k_1+k_2+k_q[Q]}{k_1+k_2} \nonumber \\[5pt] &= 1 + k_q\tau_o[Q] \nonumber \end{align} \label{10}\]

According to Equation \ref{10}, a plot of \(\tau_o/\tau\) versus \([Q]\) should be linear with an intercept equal to one, and the slope can be analyzed to obtain the bimolecular quenching rate constant, \(k_q\). Such a plot is called a Stern-Volmer plot.

In the exercise below, you will analyze fluorescent lifetime data for two different systems (each with its own quencher) and will be prompted to determine kq in each case.

Experimental Data

The following data where obtained from L.K. Fraiji, D.M. Hayes, and T.C. Werner, Journal of Chemical Education, 69(5), 424 (1992).

In the first experiment, seven aqueous solutions of the fluorescent agent N-methylacridinium iodide (N-MEAI) were prepared with increasing concentrations of a quencher, (guanosine 5'-monophosphate, disodium salt trihydrate), which is abbreviated GMP. Each sample was irradiated with a 358 nm pulsed light source and the fluorescence was recorded at 485 nm. The lifetime associated with each trial was obtained by fitting an exponential function to the measured decay curve. These lifetimes are indicated in the table below.

In the second experiment, five solutions of the fluorescent agent 1-pyrenesulfonic acid, sodium salt (PSA) were prepared with increasing concentrations iodide ion (which is an effective quenching agent for many fluorescent species). For these solutions, each sample was irradiated with a 337 nm pulsed light source and the fluorescence was recorded at 395 nm.

	N-MEAI		PSA
Trial	[GMP] - (mol/L)	τ - (ns)	[I -] - (mol/L)	τ - (ns)
1	0.0000	34.8	0.0000	58.6
2	0.0010	30.9	0.0030	37.2
3	0.0020	27.8	0.0060	26.4
4	0.0030	25.0	0.0090	20.7
5	0.0040	22.5	0.0120	17.1
6	0.0060	18.8
7	0.0080	15.7

Exercises

1. Enter each data set into an appropriate quantitative software analysis environment and generate Stern-Volmer plots for each (i.e. plot the data according to Equation \ref{10} and include a best-fit line). Is the data linear? Does the intercept equal 1 as predicted by this model? Calculate the bimolecular quenching rate constant (\(k_q\)) for each system.
2. Theories developed by the British physicist George Stokes and Albert Einstein on the topic of diffusion can be combined to obtain the Stokes-Einstein equation \[ k_d = \dfrac{8RT}{3 \eta} \label{11}\] which is useful for approximating the rate constant for diffusion limited bimolecular collisions (\(k_d\)) in solution. In this equation, \(R\) is the universal gas constant, \(T\) is absolute temperature, and \(η\) is the viscosity of the solvent. Water is the solvent employed in the fluorescence lifetime experiments presented here; the viscosity of water is η = 0.890 cP (centipoise) at 298 K [NOTE: 1 Poise = 0.1 kg/(m s)]. Use the Stokes-Einstein equation to calculate the diffusion limited bimolecular rate constant in water and compare the value you obtain to the bimolecular quenching constants (\(k_q\)) determined in step (1). Based on your comparison, what fraction of the collisions between the fluorophore and the quencher are 'effective' in actually quenching the fluorescence?
3. Independent Study: Fluorescence can be quenched by a wide range of mechanisms. The exercise performed here has focused only on 'dynamic' quenching (which is sometimes called 'collisional' quenching). 'Static' quenching represents a separate class of quenching mechanism. Consult an appropriate literature source (text or internet) and read about static quenching. Write a short paragraph that defines static quenching and how it differs from dynamic quenching.