24.2: Thermodynamics of Mixing
- Page ID
- 238274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When solids, liquids or gases are combined, the thermodynamic quantities of the system experience a change as a result of the mixing. This module will discuss the effect that mixing has on a solution’s Gibbs energy, enthalpy, and entropy, with a specific focus on the mixing of two gases.
Introduction
A solution is created when two or more components mix homogeneously to form a single phase. Studying solutions is important because most chemical and biological life processes occur in systems with multiple components. Understanding the thermodynamic behavior of mixtures is integral to the study of any system involving either ideal or non-ideal solutions because it provides valuable information on the molecular properties of the system.
Most real gases behave like ideal gases at standard temperature and pressure. This allows us to combine our knowledge of ideal systems and solutions with standard state thermodynamics in order to derive a set of equations that quantitatively describe the effect that mixing has on a given gas-phase solution’s thermodynamic quantities.
Gibbs Free Energy of Mixing
Unlike the extensive properties of a one-component system, which rely only on the amount of the system present, the extensive properties of a solution depend on its temperature, pressure and composition. This means that a mixture must be described in terms of the partial molar quantities of its components. The total Gibbs free energy of a two-component solution is given by the expression
\[ G=n_A\overline{G}_A+n_B\overline{G} _B \label{1}\]
where
- \(G\) is the total Gibbs energy of the system,
- \(n_i\) is the number of moles of component \(i\), and
- \(\overline{G}_i\) is the partial molar Gibbs energy of component \(i\).
The molar Gibbs energy of an ideal gas can be found using the equation
\[\overline{G}=\overline{G}^\circ+RT\ln \frac{P}{1\text{ bar}} \label{2}\]
where \( \overline{G}^\circ\) is the standard molar Gibbs energy of the gas at 1 bar, and P is the pressure of the system. In a mixture of ideal gases, we find that the system’s partial molar Gibbs energy is equivalent to its chemical potential, or that
\[ \overline{G}_i=\mu_i \label{3} \]
This means that for a solution of ideal gases, Equation \(\ref{2}\) can become
\[\overline{G}_i=\mu_i=\mu^\circ_i+RT \ln \frac{P_i}{1\text{ bar}} \label{4}\]
where
- \(\mu_i\) is the chemical potential of the \(i\)th component,
- \(\mu_i^\circ\) is the standard chemical potential of component \(i\) at 1 bar, and
- \(P_i\) is the partial pressure of component \(i\).
Now pretend we have two gases at the same temperature and pressure, gas A and gas B. The Gibbs energy of the system before the gases are mixed is given by Equation \(\ref{1}\), which can be combined with Equation \(\ref{4}\) to give the expression
\[G_{initial}=n_A(\mu^\circ_A+RT \ln P)+n_B(\mu^\circ_B+RT \ln P) \label{5}\]
If gas A and gas B are then mixed together, they will each exert a partial pressure on the total system, \(P_A\) and \(P_B\), so that \(P_A+ P_B= P\). This means that the final Gibbs energy of the final solution can be found using the equation
\[G_{final}=n_A(\mu^\circ_A+RT \ln P_A)+n_B(\mu^\circ_B+RT \ln P_B) \label{6}\]
The Gibbs energy of mixing, \(Δ_{mix}G\), can then be found by subtracting \(G_{initial}\) from \(G_{final}\).
\[ \begin{align} Δ_{mix}G &= G_{final} - G_{initial}\\[4pt] &=n_ART \ln \frac{P_A}{P}+n_BRT \ln \frac{P_B}{P} \\[4pt] &=n_A RT \ln X_A+n_B RT \ln X_B \label{7} \end{align} \]
where
\[P_i = X_iP\]
and \(X_i\) is the mole fraction of gas \(i\). This equation can be simplified further by knowing that the mole fraction of a component is equal to the number of moles of that component over the total moles of the system, or
\[X_i = \dfrac{n_i}{n}.\]
Equation \ref{7} then becomes
\[\Delta_{mix} G=nRT(X_A \ln X_A + X_B \ln X_B) \label{8}\]
This expression gives us the effect that mixing has on the Gibbs free energy of a solution. Since \(X_A\) and \(X_B\) are mole fractions that range from 0 to 1, we can conclude that \(Δ_{mix}G \) will be a negative number. This is consistent with the idea that gases mix spontaneously at constant pressure and temperature.
Entropy of mixing
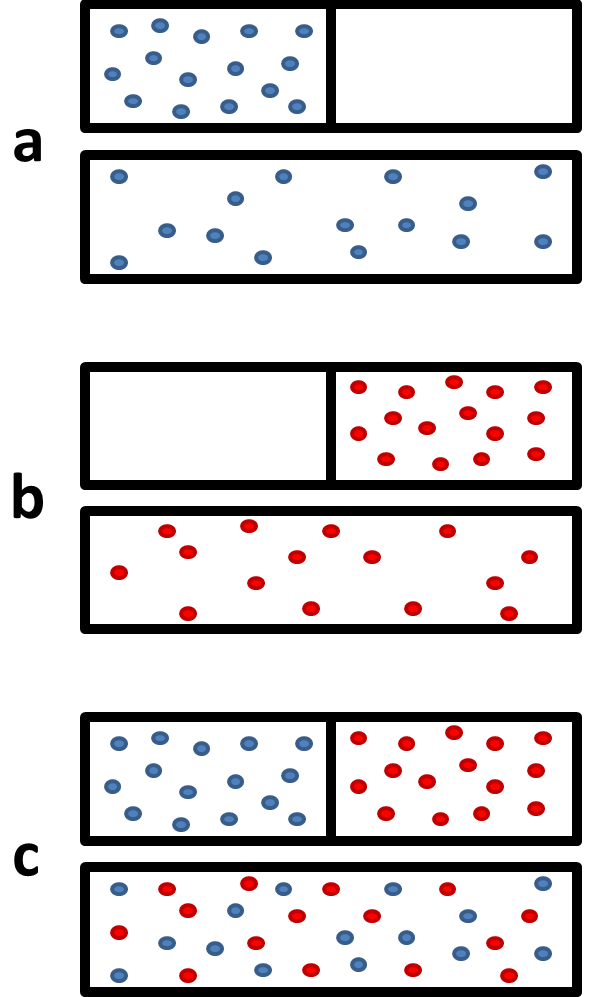
Figure \(\PageIndex{1}\) shows that when two gases mix, it can really be seen as two gases expanding into twice their original volume. This greatly increases the number of available microstates, and so we would therefore expect the entropy of the system to increase as well.
Thermodynamic studies of an ideal gas’s dependence of Gibbs free energy of temperature have shown that
\[ \left( \dfrac {d G} {d T} \right )_P=-S \label{9}\]
This means that differentiating Equation \(\ref{8}\) at constant pressure with respect to temperature will give an expression for the effect that mixing has on the entropy of a solution. We see that
\[ \begin{align} \left( \dfrac {d G_{mix}} {d T} \right)_P &=nR(X_A \ln X_A+X_B \ln X_B) \\[4pt] &=-\Delta_{mix} S \end{align}\]
\[\Delta_{mix} S=-nR(X_A \ln X_A+X_2 \ln X_2) \label{10}\]
Since the mole fractions again lead to negative values for \(\ln X_A\) and \(\ln X_B\), the negative sign in front of the equation makes \(\Delta_{mix} S\) positive, as expected. This agrees with the idea that mixing is a spontaneous process.
Enthalpy of mixing
We know that in an ideal system \(\Delta G= \Delta H-T \Delta S\), but this equation can also be applied to the thermodynamics of mixing and solved for the enthalpy of mixing so that it reads
\[\Delta_{mix} H=\Delta_{mix} G+T\Delta_{mix} S \label{11}\]
Plugging in our expressions for \(Δ_{mix}G\) (Equation \(\ref{8}\)) and \(Δ_{mix}S\) (Equation \(\ref{10}\)) , we get
\[\Delta_{mix} H=nRT(X_A \ln X_A+X_B \ln X_B)+T \left[-nR(X_A \ln X_A+X_B \ln X_B) \right] = 0\]
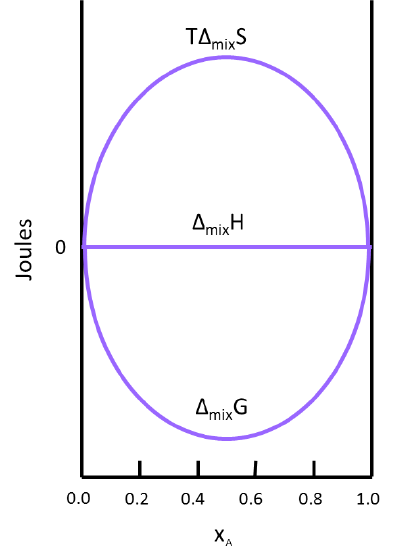
This result makes sense when considering the system. The molecules of ideal gas are spread out enough that they do not interact with one another when mixed, which implies that no heat is absorbed or produced and results in a \(Δ_{mix}H\) of zero. Figure \(\PageIndex{2}\) illustrates how \(TΔ_{mix}S\) and \(Δ_{mix}G\) change as a function of the mole fraction so that \(Δ_{mix}H\) of a solution will always be equal to zero (this is for the mixing of two ideal gasses).
References
- Chang, R. Physical Chemistry for the Biosciences, 1st Herdon, VA: University Science Books, 132-133. Print.
- Meyer, E.F. (1987). Theromodynamics of “Mixing” of Ideal Gases. J. Chem. Educ. 64, 676-677.
Outside Links
- Satter, S. (2000). Thermodynamics of Mixing Real Gases. J. Chem. Educ. 77, 1361-1365.
- Brandani, V., Evangelista, F. (1987). Correlation and prediction of enthalpies of mixing for systems containing alcohols with UNIQUAC associated-solution theory. Ind. Eng. Chem. Res. 26 (12), 2423–2430.
Problems
- Use Figure 2 to find the x1 that has the largest impact on the thermodynamic quantities of the final solution. Explain why this is true.
- Calculate the effect that mixing 2 moles of nitrogen and 3 moles of oxygen has on the entropy of the final solution.
- Another way to find the entropy of a system is using the equation ΔS = nRln(V2/V1). Use this equation and the fact that volume is directly proportional to the number of moles of gas at constant temperature and pressure to derive the final expression for \(T\Delta_{mix}S\) . (Hint: Use the derivation of \(T\Delta_{mix}G\) as a guide).
Answers
- x1= 0.5
- Increases the entropy of the system by 27.98 J/molK
Contributors
- Elizabeth Billquist (Hope College)

