7.1: The Molecular Basis for Understanding Simple Entropy Change
- Page ID
- 238717
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quantization of the motional energy of molecules
Early in their discussion of kinetic-molecular theory, most general chemistry texts have a Figure of the greatly increased distribution of molecular speeds at higher temperatures in gases than at moderate temperatures.
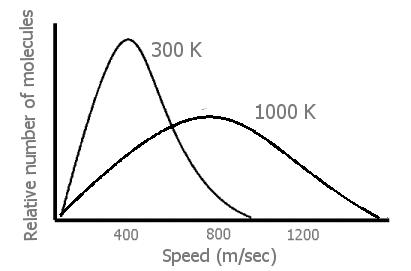
When the temperature of a gas is raised (by transfer of energy from the surroundings of the system), there is a great increase in the velocity, \(v\), of many of the gas molecules (Figure \(\PageIndex{1}\)). From 1/2mv2, this means that there has also been a great increase in the translational energies of those faster moving molecules. Finally, we can see that an input of energy not only causes the gas molecules in the system to move faster — but also to move at very many different fast speeds. (Thus, the energy in a heated system is more dispersed, spread out in being in many separate speeds rather than more localized in fewer moderate speeds.)
A symbolic indication of the different distributions of the translational energy of each molecule of a gas on low to high energy levels in a 36-molecule system is in Figure \(\PageIndex{2}\), with the lower temperature gas as Figure \(\PageIndex{2A}\) and the higher temperature gas as Figure \(\PageIndex{2B}\).
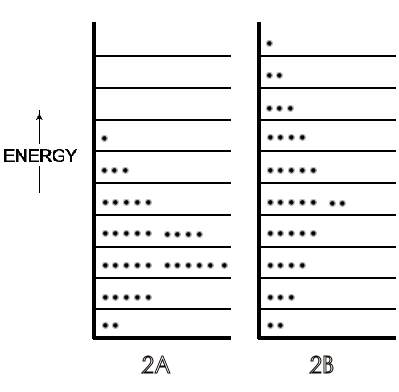
These and later Figures in this section are symbolic because, in actuality, this small number of molecules is not enough to exhibit thermodynamic temperature. For further simplification, rotational energies that range from zero in monatomic molecules to about half the total translational energy of di- and tri-atomic molecules (and more for most polyatomic) at 300 K are not shown in the Figures. If those rotational energies were included, they would constitute a set of energy levels (corresponding to a spacing of ~10-23 J) each with translational energy distributions of the 36 molecules (corresponding to a spacing of ~10-37 J). These numbers show why translational levels, though quantized, are considered virtually continuous compared to the separation of rotational energies. The details of vibrational energy levels — two at moderate temperatures (on the ground state of which would be almost all the rotational and translational levels populated by the molecules of a symbolic or real system) — can also be postponed until physical chemistry. At this point in the first year course, depending on the instructor's preference, only a verbal description of rotational and vibrational motions and energy level spacing need be introduced.
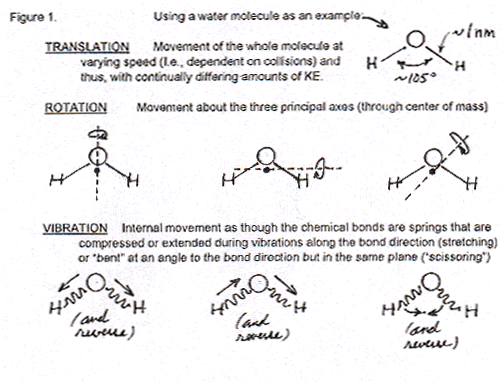
By the time in the beginning course that students reach thermodynamics, five to fifteen chapters later than kinetic theory, they can accept the concept that the total motional energies of molecules includes not just translational but also rotational and vibrational movements (that can be sketched simply below).
A microstate is one of many arrangements of the molecular energies (i.e., ‘the molecules on each particular energy level') for the total energy of a system. Thus, Figure \(\PageIndex{2A}\) is one microstate for a system with a given energy and Figure \(\PageIndex{1B}\) is a microstate of the same system but with a greater total energy. Figure \(\PageIndex{3A}\) (just a repeat of Figure \(\PageIndex{2A}\), for convenience) is a different microstate than the microstate for the same system shown in Figure \(\PageIndex{3B}\); the total energy is the same in \(\PageIndex{3A}\) and \(\PageIndex{3B}\), but in Figure \(\PageIndex{3B}\) the arrangement of energies has been changed because two molecules have changed their energy levels, as indicated by the arrows.
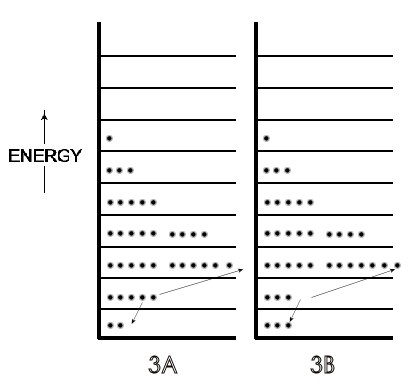
A possible scenario for that different microstate in Figure \(\PageIndex{3}\) is that these two molecules on the second energy level collided at a glancing angle such that one gained enough energy to be on the third energy level, while the other molecule lost the same amount of energy and dropped down to the lowest energy level. In the light of that result of a single collision and the billions of collisions of molecules per second in any system at room temperature, there can be a very large number of microstates even for this system of just 36 molecules in Figures \(\PageIndex{2}\) and \(\PageIndex{3}\). (This is true despite the fact that not every collision would change the energy of the two molecules involved, and thus not change the numbers on a given energy level. Glancing collisions could occur with no change in the energy of either participant.) For any real system involving 6 x 1023 molecules, however, the number of microstates becomes humanly incomprehensible for any system, even though we can express it in numbers, as will now be developed.
The quantitative entropy change in a reversible process is given by
\[ΔS = \dfrac{q_{rev}}{T}\]
(Irreversible processes involving temperature or volume change or mixing can be treated by calculations from incremental steps that are reversible.) According to the Boltzmann entropy relationship,
\[ΔS = k \ln \dfrac{W_{Final}}{W_{Initial}}\]
where \(k\) is Boltzmann's constant and \(W_{Final}\) or \(W_{Initial}\) is the count of how many microstates correspond to the Final or Initial macrostates, respectively.
The number of microstates for a system determines the number of ways in any one of which that the total energy of a macrostate can be at one instant. Thus, an increase in entropy means a greater number of microstates for the Final state than for the Initial. In turn, this means that there are more choices for the arrangement of a system's total energy at any one instant, far less possibility of localization (such as cycling back and forth between just 2 microstates), i.e., greater dispersal of the total energy of a system because of so many possibilities.
An increase in entropy means a greater number of microstates for the Final state than for the Initial. In turn, this means that there are more choices for the arrangement of a system's total energy at any one instant.
Delocalization vs. Dispersal
Some instructors may prefer “delocalization” to describe the status of the total energy of a system when there are a greater number of microstates rather than fewer, as an exact synonym for “dispersal” of energy as used here in this article for other situations in chemical thermodynamics. The advantage of uniform use of ‘dispersal' is its correct common-meaning applicability to examples ranging from motional energy becoming literally spread out in a larger volume to the cases of thermal energy transfer from hot surroundings to a cooler system, as well as to distributions of molecular energies on energy levels for either of those general cases. Students of lesser ability should be able to grasp what ‘dispersal' means in three dimensions, even though the next steps of abstraction to what it means in energy levels and numbers of microstates may result in more of a ‘feeling' than a preparation for physical chemistry that it can be for the more able.
Of course, dispersal of the energy of a system in terms of microstates does not mean that the energy is smeared or spread out over microstates like peanut butter on bread! All the energy of the macrostate is always in only one microstate at one instant. It is the possibility that the total energy of the macrostate can be in any one of so many more different arrangements of that energy at the next instant — an increased probability that it could not be localized by returning to the same microstate — that amounts to a greater dispersal or spreading out of energy when there are a larger number of microstates
(The numbers of microstates for chemical systems above 0 K are astounding. For any substance at a temperature about 1-4 K, there are 1026,000,000,000,000,000,000 microstates (5). For a mole of water at 273.15 K, there are 102,000,000,000,000,000,000,000,000 microstates and when it is heated to be just one degree warmer, that number is increased 1022 times to 102,010,000,000,000,000,000,000,000 microstates. For comparison, an estimate of the number of atoms in the entire universe is ‘only' about 1070, while a googol, considered a large number in mathematics, is `only' 10100.)
Summarizing, when a substance is heated, its entropy increases because the energy acquired and that previously within it can be far more dispersed on the previous higher energy levels and on those additional high energy levels that now can be occupied. This in turn means that there are many many more possible arrangements of the molecular energies on their energy levels than before and thus, there is a great increase in accessible microstates for the system at higher temperatures. A concise statement would be that when a system is heated, there are many more microstates accessible and this amounts to greater delocalization or dispersal of its total energy. (The common comment "heating causes or favors molecular disorder" is an anthropomorphic labeling of molecular behavior that has more flaws than utility. There is virtual chaos, so far as the distribution of energy for a system (its number of microstates) is concerned, before as well as after heating at any temperature above 0 K and energy distribution is at the heart of the meaning of entropy and entropy change. ) (5).

