7.2: The Hamiltonian Operator for Rotational Motion
- Page ID
- 4518
We start our consideration of rotational motion with a system consisting of two atoms connected by a rigid bond, shown in Figure \(\PageIndex{1}\). Translational motion can be separated from rotational motion if we specify the position of the center of mass by a vector \(R\), and the positions of each atom relative to the center of mass by vectors \(r_1\) and \(r_2\). The positions of the atoms then are given by \(R + r_1\) and \(R + r_2\). The motion of the two particles is described as the translational motion of the center of mass plus the rotational motion of the two particles around the center of mass.
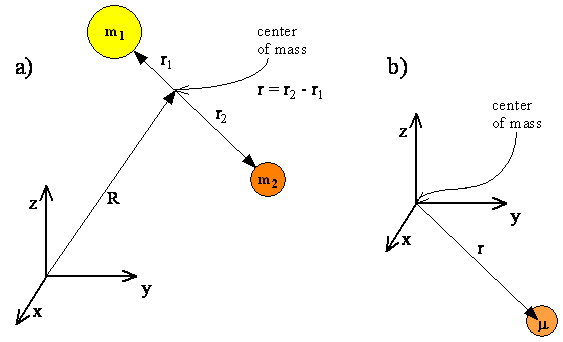
The quantum mechanical description of translational motion, which corresponds to a free particle with total mass \(m_1 + m_2\), was described in Chapter 5. Since translational motion and rotational motion are separable, i.e. independent, the translational and rotational energies will add, and the total wavefunction will be a product of a translational function and a rotational function.
Exercise \(\PageIndex{1}\)
What do you need to know in order to write the Hamiltonian for the rigid rotor?
We start our quantum mechanical description of rotation with the Hamiltonian:
\[\hat {H} = \hat {T} + \hat {V} \label {7.1}\]
To explicitly write the components of the Hamiltonian operator, first consider the classical energy of the two rotating atoms and then transform the classical momentum that appears in the energy equation into the equivalent quantum mechanical operator. In the classical analysis the rotational motion of two particles separated by a distance \(r\) can be treated as a single particle with reduced mass \(μ\) at a distance \(r\) from the center of rotation, which is the center of mass.
The kinetic energy of the reduced particle is
\[ T = \dfrac {p^2}{2 \mu} \label {7-2}\]
where
\[ P^2 = P^2_x + P^2_y + P^2_z \label {7-3}\]
Transforming \(T\) to a quantum-mechanical operator yields
\[ \hat {T} = - \dfrac {\hbar ^2 \nabla ^2}{2 \mu} \label {7-4}\]
where \(\nabla ^2\) is the Laplacian operator.
\[\nabla ^2 = \dfrac {\partial ^2}{\partial x^2} + \dfrac {\partial ^2}{\partial y^2} + \dfrac {\partial ^2}{\partial z^2} \label {7-5}\]
The rigid rotor model does not include the presence of electric or magnetic fields, or any other external force. Since there are no forces acting on the rotating particle, the potential energy is constant, and we can set it to zero or to any other value because only changes in energy are significant, and there is no absolute zero of energy.
\[ \hat {V} = 0 \label {7-6}\]
Therefore, the Hamiltonian operator for the Schrödinger equation describing this system consists only of the kinetic energy term.
\[ \hat {H} = \hat {T} + \hat {V} = - \dfrac {\hbar ^2 \nabla ^2}{2 \mu} \label {7-7}\]
In Equation \ref{7-5} we wrote the Laplacian operator in Cartesian coordinates. Cartesian coordinates (x, y, z) describe position and motion relative to three axes that intersect at 90º. They work fine when the geometry of a problem reflects the symmetry of lines intersecting at 90º, but the Cartesian coordinate system is not so convenient when the geometry involves objects going in circles as in the rotation of a molecule. In this case, spherical coordinates \((r,\,\theta,\,\phi)\) shown in Figure \(\PageIndex{2}\) are better.

The limits of these coordinantes are
- \(0 \le r < \infty\)
- \(0 \le \theta < \pi\)
- \(0 \le \varphi < 2\pi\)
Spherical coordinates are better because they reflect the spherical symmetry of a rotating molecule. Spherical coordinates have the advantage that motion in a circle can be described by using only a single coordinate. For example, as shown in Figure \(\PageIndex{2}\), changing φ describes rotation around the z‑axis. Changing \(θ\) also is very simple. It describes rotation in any plane containing the z‑axis, and \(r\) describes the distance from the origin for any value of \(θ\) and \(φ\).
This situation is analogous to choosing Cartesian or spherical coordinates to locate rooms in a building. Cartesian coordinates are excellent if the building is designed with hallways intersecting at 90º and with an elevator running perpendicular to the floors. Cartesian coordinates would be awkward to use for addresses in a spherical satellite space station with spherical hallways at various distances from the center.
Exercise \(\PageIndex{2}\)
Imagine and draw a sketch of a spherical space station with spherical shells for hallways. Show how three spherical coordinates can be used to specify the address of a particular room in terms of values for \(r\), \(θ\), and \(φ\).
In order to use spherical coordinates, we need to express \(\nabla ^2\) in terms of \(r\), \(θ\) and \(θ\) and \(φ\). The result of the coordinate transformation is
\[\nabla ^2 = \dfrac {1}{r^2} \left ( \dfrac {\partial}{\partial r} r^2 \dfrac {\partial}{\partial r} + \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta} \sin \theta \dfrac {\partial}{\partial \theta} + \dfrac {1}{\sin ^2 \theta } \dfrac {\partial ^2}{\partial \varphi ^2} \right ) \label {7-19}\]
The Hamiltonian operator in spherical coordinates now becomes
\[ \hat {H} = \dfrac {-\hbar ^2}{2 \mu r^2} [\dfrac {\partial}{\partial r} r^2 \dfrac {\partial}{\partial r} + \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta} \sin \theta \dfrac {\partial}{\partial \theta} + \dfrac {1}{\sin ^2 \theta } \dfrac {\partial ^2}{\partial \varphi ^2}] \label {7-11}\]
This version of the Hamiltonian looks more complicated than Equation \ref{7-7}, but it has the advantage of using variables that are separable (see Separation of Variables). As you may recall, when the variables are separable, the Schrödinger equation can be written as a sum of terms, with each term depending only on a single variable, and the wavefunction solutions are products of functions that each depend on only one variable.


