7.1: Introduction to Rotation
- Page ID
- 7135
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
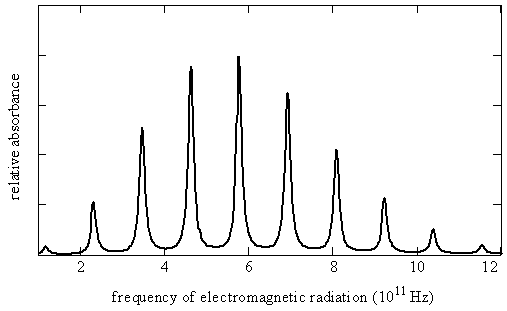
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecules rotate as well as vibrate. Transitions between rotational energy levels in molecules generally are found in the far infrared and microwave regions of the electromagnetic spectrum. A rotational spectrum of a simple diatomic molecule is illustrated in Figure \(\PageIndex{1}\) and quantitative information about this spectrum is given in Table \(\PageIndex{2}\) near the end of this chapter. Notice that the lines are nearly equally spaced and vary in intensity. In this chapter, we will see that the magnitude of the molecule's moment of inertia causes rotational transitions to lie in these spectral regions. We also will learn why the lines are nearly equally spaced and vary in intensity. Such spectra can be used to determine bond lengths, and even bond angles in polyatomic molecules.
To develop a description of the rotational states, we will consider the molecule to be a rigid object, i.e. the bond lengths are fixed and the molecule cannot vibrate. This model for rotation is called the rigid-rotor model. It is a good approximation (even though a molecule vibrates as it rotates, and the bonds are elastic rather than rigid) because the amplitude of the vibration is small compared to the bond length.
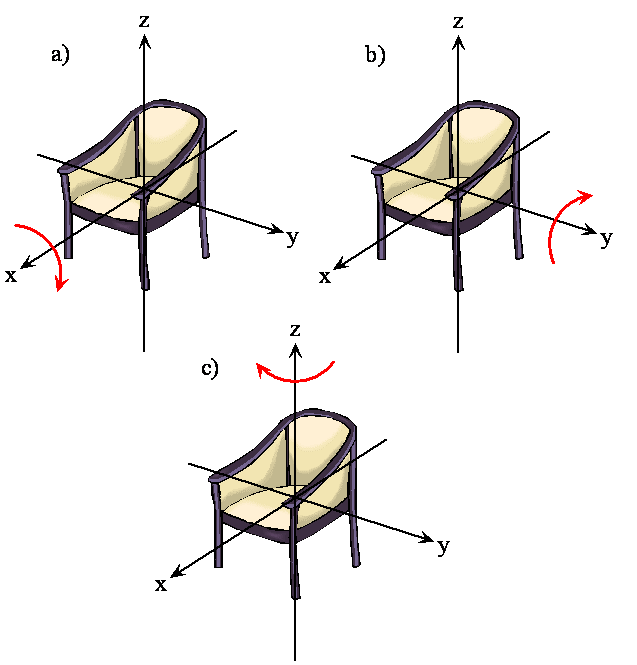
The rotation of a rigid object in space is very simple to visualize. Pick up any object and rotate it. There are orthogonal rotations about each of the three Cartesian coordinate axes just as there are orthogonal translations in each of the directions in three-dimensional space; see Figures \(\PageIndex{2}\) and \(\PageIndex{3}\). The rotations are said to be orthogonal because one can not describe a rotation about one axis in terms of rotations about the other axes just as one can not describe a translation along the x-axis in terms of translations along the y- and z-axes. For a linear molecule, the motion around the interatomic axis (x-axis) is not a rotation.
In this chapter we consider the case of a diatomic molecule. Solving the Schrödinger equation for rotational motion will give us the rotational energies and angular momenta, the wavefunctions associated with these energy levels and angular momenta, and the quantum numbers that serve to label the energy levels, angular momenta, and wavefunctions. The quantum numbers appear because of boundary conditions imposed on the wavefunctions.

We will find that the energy of rotation is quantized. This quantization and the selection rules for spectroscopic transitions between the various energy levels lead to the absorption lines seen in the rotational spectrum in Figure \(\PageIndex{1}\). The angular momentum also is quantized, which means that only certain values of the angular momentum are possible, and, when some direction is uniquely defined by an electric or magnetic field, only certain orientations of the rotating molecule in space are possible. This restriction on orientation is called space quantization.
As you can see in Figure \(\PageIndex{4}\) and Exercise \(\PageIndex{1}\), the angular momentum vector for a classical rotating system is perpendicular to the plane of rotation. The direction of the vector is given by applying the right-hand rule to the direction of rotation. The orientation of a classical rotating diatomic molecule therefore is defined by the plane in which the internuclear axis lies during rotation or by the direction of the angular momentum vector, which is perpendicular to this plane. The direction of the angular momentum vector is called the axis-of-rotation. Angular momentum vectors are useful because they provide a shorthand way to represent the classical motion of a rotating diatomic molecule. Given only an angular momentum vector, it is possible to reconstruct the direction and plane of rotation in addition to the magnitude of the angular momentum, which is in turn a function of the reduced mass, bond length, and angular velocity of the rotating molecule.
The material in this chapter is very important because the wavefunctions obtained by solving the Schrödinger equation for rotational motion also will be used to describe the hydrogen atom in the next chapter. The hydrogen atom wavefunctions, in turn, are the key to understanding atomic and molecular structure and chemical reactivity.
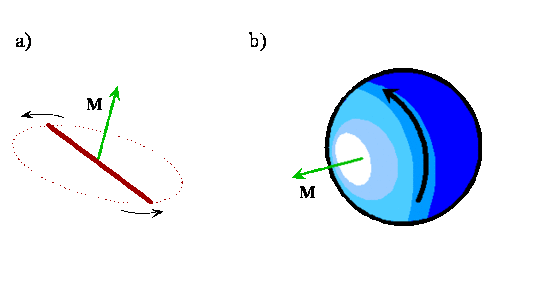
Exercise \(\PageIndex{1}\)
To visualize these different orientations and the axis-of-rotation, use your pencil to represent the internuclear axis of a diatomic molecule, rotate it in different planes and align another pencil along the axis-of-rotation in each case.


