9.5: Single-electron Wavefunctions and Basis Functions
- Page ID
- 4534
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Finding the most useful single-electron wavefunctions to serve as building blocks for a multi-electron wavefunction is one of the main challenges in finding approximate solutions to the multi-electron Schrödinger Equation. The functions must be different for different atoms because the nuclear charge and number of electrons are different. The attraction of an electron for the nucleus depends on the nuclear charge, and the electron-electron interaction depends upon the number of electrons.
As we saw in our initial approximation methods, the most straightforward place to start in finding reasonable single-electron wavefunctions for multi-electron atoms is with the atomic orbitals produced in the quantum treatment of hydrogen, the so-called “hydrogenic” spin-orbitals. These traditional atomic orbitals, with a few modifications, give quite reasonable calculated results and are still in wide use for conceptually understanding multi-electron atoms. In this section and in Chapter 10 we will explore some of the many other single-electron functions that also can be used as atomic orbitals.
Hydrogenic spin-orbitals used as components of multi-electron systems are identified in the same way as they are for the hydrogen atom. Each spin-orbital consists of a spatial wavefunction, specified by the quantum numbers (n, \(l , m_l\)) and denoted ls, 2s, 2p, 3s, 3p, 3d, etc, multiplied by a spin function, specified by the quantum number \(m_s\) and denoted \(\alpha\) or \(\beta\). In our initial approximation methods, we ignored the spin components of the hydrogenic orbitals, but they must be considered in order to develop a complete description of multi-electron systems. The subscript on the argument of the spatial function reveals which electron is being described (\(r_1\) is a vector that refers to the coordinates of electron 1, for example.) No argument is given for the spin function. An example of a spin-orbital for electron 2 in a \(3p_z\) orbital:
\[ | \varphi _{3p_z} \alpha (r_2) \rangle = \varphi _{3,1,0}(r_2) \alpha \label {9.5.1}\]
In the alternative shorthand notation for this spin-orbital shown below, the coordinates for electron 2 in the spatial function are abbreviated simply by the number “2,” and the spatial function is represented by “\(3p_z\)” rather than "\(\varphi _{3,1,0}\)". The argument “2” given for the spin function refers to the unknown spin variable for electron 2. Many slight variations on these shorthand forms are in use in this and other texts, so flexibility and careful reading are important.
\[ | \varphi _{3p_z}\alpha (2) \rangle = 3p_z (2) \alpha (2) \label {9.5.2}\]
In this chapter we will continue the trend of moving away from writing specific mathematical functions and toward a more symbolic, condensed representation. Your understanding of the material in this and future chapters requires that you keep in mind the form and properties of the specific functions denoted by the symbols used in each equation.
Exercise \(\PageIndex{1}\)
Write the full mathematical form of \(\varphi _{3pz\alpha}\) using as much explicit functional detail as possible.
The basic mathematical functions and thus the general shapes and angular momenta for hydrogenic orbitals are the same as those for hydrogen orbitals. The differences between atomic orbitals for the hydrogen atom and those used as components in the wavefunctions for multi-electron systems lie in the radial parts of the wavefunctions and in the energies. Specifically, the differences arise from the replacement of the nuclear charge Z in the radial parts of the wavefunctions by an adjustable parameter \(\zeta\) that is allowed to vary in approximation calculations in order to model the interactions between the electrons. We discussed such a procedure for helium The Variational Method previously. The result is that electrons in orbitals with different values for the angular momentum quantum number, \(l\), have different energies. Figure \(\PageIndex{1}\) shows the results of a quantum mechanical calculation on argon in which the degeneracy of the 2s and 2p orbitals is found to be removed, as is the degeneracy of the 3s, 3p, and 3d orbitals.
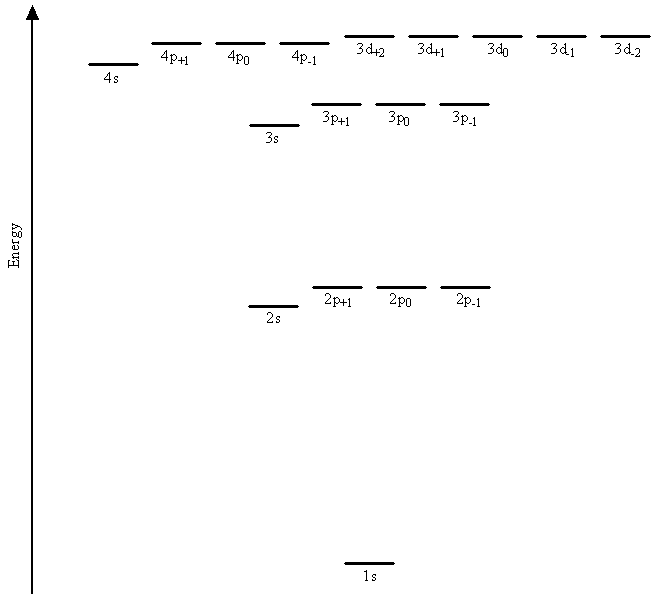
The energy of each electron now depends not only on its principal quantum number, \(n\), but also on its angular momentum quantum number, \(l\).
The presence of \(\zeta\) in the radial portions of the wavefunctions also means that the electron probability distributions associated with hydrogenic atomic orbitals in multi-electron systems are different from the exact atomic orbitals for hydrogen. Figure \(\PageIndex{2}\) compares the radial distribution functions for an electron in a 1s orbital of hydrogen (the ground state), a 2s orbital in hydrogen (an excited configuration of hydrogen) and a 1s orbital in helium that is described by the best variational value of \(\zeta\). Our use of hydrogen-like orbitals in quantum mechanical calculations for multi-electron atoms helps us to interpret our results for multi-electron atoms in terms of the properties of a system we can solve exactly.
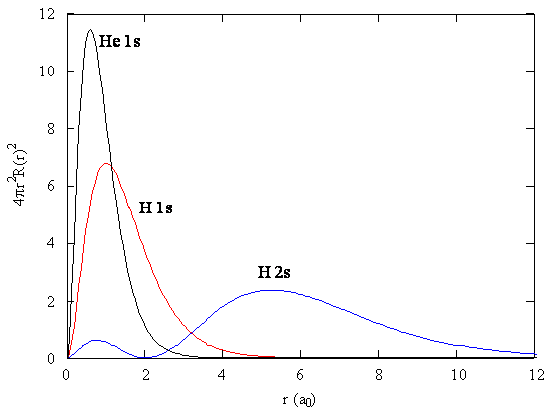
Exercise \(\PageIndex{2}\)
Analyze Figure \(\PageIndex{2}\) and write a paragraph about what you can discern about the relative sizes of ground state hydrogen, excited state hydrogen and ground state helium atoms.
While they provide useful stepping off points for understanding computational results, nothing requires us to use the hydrogenic functions as the building blocks for multi-electrons wavefunctions. In practice, the radial part of the hydrogenic atomic orbital presents a computational difficulty because the radial function has nodes, positive and negative lobes, and steep variations that make accurate evaluation of integrals by a computer slow. Consequently other types of functions are generally used in building multi-electron functions. These usually are related to the hydrogenic orbitals to aid in the analysis of molecular electronic structure. For example, Slater-type atomic orbitals (STO’s), designated below as \(S_{nlm} (r, \theta , \varphi )\), avoid the difficulties imposed by the hydrogenic functions. The STO’s, named after their creator, John Slater, were the first alternative functions that were used extensively in computations. STO’s do not have any radial nodes, but still contain a variational parameter \(\zeta\) (zeta), that corresponds to the effective nuclear charge in the hydrogenic orbitals. In Equation \(\ref{9-36}\) and elsewhere in this chapter, the distance, \(r\), is measured in units of the Bohr radius, \(a_0\).
\[ S_{nlm} (r, \theta , \varphi ) = \dfrac {(2 \zeta )^{n+1/2}}{[(2n)!]^{1/2}} r^{n-1} e^{-\zeta r } Y^m_l (\theta , \varphi ) \label {9-36}\]
Exercise \(\PageIndex{3}\)
- Write the radial parts of the 1s, 2s, and 2p atomic orbitals for hydrogen.
- Write the radial parts of the n = 1 and n = 2 Slater–type orbitals (STO).
- Check that the above five functions are normalized.
- Graph these five functions, measuring r in units of the Bohr radius.
- Graph the radial probability densities for these orbitals. Put the hydrogen orbital and the corresponding STO on the same graph so they can be compared easily.
- Adjust the zeta parameter \(\zeta\) in each case to give the best match of the radial probability density for the STO with that of the corresponding hydrogen orbital.
- Comment on the similarities and differences between the hydrogen orbitals and the STOs and the corresponding radial probability densities.
Linear Variational Method
An alternative approach to the general problem of introducing variational parameters into wavefunctions is the construction of a single-electron wavefunction as a linear combination of other functions. For hydrogen, the radial function decays, or decreases in amplitude, exponentially as the distance from the nucleus increases. For helium and other multi-electron atoms, the radial dependence of the total probability density does not fall off as a simple exponential with increasing distance from the nucleus as it does for hydrogen. More complex single-electron functions therefore are needed in order to model the effects of electron-electron interactions on the total radial distribution function. One way to obtain more appropriate single-electron functions is to use a sum of exponential functions in place of the hydrogenic spin-orbitals.
An example of such a wavefunction created from a sum or linear combination of exponential functions is written as
\[ \varphi _{1s} (r_1) = \sum _j c_j e^{-\zeta _j r_j /a_o} \label{9-37}\]
The linear combination permits weighting of the different exponentials through the adjustable coefficients (cj) for each term in the sum. Each exponential term has a different rate of decay through the zeta-parameter \(\zeta _j\). The exponential functions in Equation \(\ref{9-37}\) are called basis functions. Basis functions are the functions used in linear combinations to produce the single-electron orbitals that in turn combine to create the product multi-electron wavefunctions. Originally the most popular basis functions used were the STO’s, but today STO’s are not used in most quantum chemistry calculations. However, they are often the functions to which more computationally efficient basis functions are fitted.
Physically, the \(\zeta _j\) parameters account for the effective nuclear charge (often denoted with \(Z_{eff}\). The use of several zeta values in the linear combination essentially allows the effective nuclear charge to vary with the distance of an electron from the nucleus. This variation makes sense physically. When an electron is close to the nucleus, the effective nuclear charge should be close to the actual nuclear charge. When the electron is far from the nucleus, the effective nuclear charge should be much smaller. See Slater's rules for a rule-of-thumb approach to evaluate \(Z_{eff}\) values.
A term in Equation \(\ref{9-37}\) with a small \(\zeta\) will decay slowly with distance from the nucleus. A term with a large \(\zeta\) will decay rapidly with distance and not contribute at large distances. The need for such a linear combination of exponentials is a consequence of the electron-electron repulsion and its effect of screening the nucleus for each electron due to the presence of the other electrons.
Exercise \(\PageIndex{4}\)
Make plots of \(\varphi\) in Equation \(\ref{9-37}\) using three equally weighted terms with \(\zeta\) = 1.0, 2.0, and 5.0. Also plot each term separately.
Computational procedures in which an exponential parameter like \(\zeta\) is varied are more precisely called the Nonlinear Variational Method because the variational parameter is part of the wavefunction and the change in the function and energy caused by a change in the parameter is not linear. The optimum values for the zeta parameters in any particular calculation are determined by doing a variational calculation for each orbital to minimize the ground-state energy. When this calculation involves a nonlinear variational calculation for the zetas, it requires a large amount of computer time. The use of the variational method to find values for the coefficients, \(\{c_j\}\), in the linear combination given by Equation \(\ref{9-37}\) above is called the Linear Variational Method because the single-electron function whose energy is to be minimized (in this case \(\varphi _{1s}\)) depends linearly on the coefficients. Although the idea is the same, it usually is much easier to implement the linear variational method in practice.
Nonlinear variational calculations are extremely costly in terms of computer time because each time a zeta parameter is changed, all of the integrals need to be recalculated. In the linear variation, where only the coefficients in a linear combination are varied, the basis functions and the integrals do not change. Consequently, an optimum set of zeta parameters were chosen from variational calculations on many small multi-electron systems, and these values, which are given in Table \(\PageIndex{1}\), generally can be used in the STOs for other and larger systems.
| Atom | \(\zeta _{1s}\) | \(\zeta _{2s,2p}\) |
|---|---|---|
| H | 1.24 | |
| He | 1.69 | |
| Li | 2.69 | 0.80 |
| Be | 3.68 | 1.15 |
| B | 4.68 | 1.50 |
| C | 5.67 | 1.72 |
| N | 6.67 | 1.95 |
| O | 7.66 | 2.25 |
| F | 8.56 | 2.55 |
| Ne | 9.64 | 2.88 |
Exercise \(\PageIndex{5}\)
Compare the value \(\zeta _{1s}\) = 1.24 in Table \(\PageIndex{1}\) for hydrogen with the value you obtained in Exercise \(\PageIndex{3}\). and comment on possible reasons for any difference. Why are the zeta values larger for 1s than for 2s and 2p orbitals? Why do the \(\zeta _{1s}\) values increase by essentially one unit for each element from He to Ne while the increase for the \(\zeta _{2s, 2p}\) values is much smaller?
The discussion above gives us some new ideas about how to write flexible, useful single-electron wavefunctions that can be used to construct multi-electron wavefunctions for variational calculations. Single-electron functions built from the basis function approach are flexible because they have several adjustable parameters, and useful because the adjustable parameters still have clear physical interpretations. Such functions will be needed in the Hartree-Fock method discussed elsewhere.


