7.5: Quantum Mechanical Properties of Rotating Diatomic Molecules
- Page ID
- 4515
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we examine the rotational states for a diatomic molecule by comparing the classical interpretation of the angular momentum vector with the probabilistic interpretation of the angular momentum wavefunctions. We want to answer the following types of questions. How do we describe the orientation of a rotating diatomic molecule in space? Is the molecule actually rotating? What properties of the molecule can be physically observed? In what ways does the quantum mechanical description of a rotating molecule differ from the classical image of a rotating molecule?
Introduction
In isotropic space, meaning all directions are equivalent, any given molecule can have any orientation. The z-axis can have any orientation. Since we cannot distinguish different directions in isotropic space, different molecules will have different angular momentum vectors and all orientations of these vectors in space will be equally probable. Thus for example, even though our quantum mechanical description says that only three states with different angular momentum and internuclear axis orientations are allowed for the \(J = 1\) energy level (\(m_J = 0, 1, -1\)), there are no practical consequences of this fact in isotropic space.
We can make space anisotropic by applying an external field, e.g. an electric field or a magnetic field. The field direction is a unique direction in space, and it is most convenient to assign the z-axis to that direction. Our rotational wavefunctions and operators implicitly are designed to have z be the special axis because of the relationships between the spherical coordinates and the Cartesian coordinates. The effects of external electric and magnetic fields on atomic and molecular spectra is an active area of research that has provided much insight into the properties of atoms and molecules and the use of quantum mechanics to describe them. For example, magnetic field effects on atomic spectra contributed to the discovery of electron spin and are discussed in the next chapter. These effects are known as Stark effects (electric field) and Zeeman effects (magnetic field) after the pioneers who discovered them.
For the ground state, J = 0, the rotational energy and angular momentum are zero. With no rotational energy or angular momentum, the molecule cannot be rotating! It may be vibrating and translating, but it is not rotating. What is its orientation in space? Examine the wavefunction in Figure \(\PageIndex{9}\). All values of \(\theta\) and \(\varphi\) are equally probable; we have no information about the orientation of the molecule in this state. The fact that there is no uncertainty in the angular momentum (it is exactly zero), and no information about the orientation (the uncertainty is infinite) is consistent with the Heisenberg Uncertainty Principle.
The space for a rigid rotor is defined by all the values for the variables \(\theta\) and \(\varphi\). Since a rigid rotor is not constrained to any region of this space by a potential boundary, the energy and angular momentum can be zero because the uncertainty in the location of the rotor in this space is infinite. The rotor can be anywhere; \(\theta\) and \(\varphi\) can have any values. This situation is analogous to the free particle, where we knew the momentum exactly but had no knowledge of the particle's position. When \(J\) is different from 0, the uncertainty in the location of the rotor decreases. It is more likely to be found in some regions of space than in others. This decrease in uncertainty about the location of the rotor is accompanied by an increase in the uncertainty in the angular momentum as required by the Uncertainty Principle. We still know the magnitude of the angular momentum vector exactly, but its direction in space is uncertain.
Next consider the case \(J = l\) with \(m_J = +1, 0, -1\). The length of the angular momentum vectors for all of these states is \(\sqrt {2} \hbar\), see Exercise \(\PageIndex{16}\) and Figure \(\PageIndex{11}\). From a classical perspective, the non-zero value for angular momentum means that the molecule must be rotating. The projections of the vectors onto the z-axis are ħ, 0, and -ħ for the \(m_J = +1, 0, -1\) states, respectively. The classical interpretation of this result is that, while the plane of rotation of the molecule, which is perpendicular to the angular momentum vector describing each state, is confined to a specific orientation with respect to the z-axis, it is not confined with respect to the x- and y- axes.
The classical picture of rotation and interpretation of the angular momentum vector for the J = 1, \(m_J = 0\) state places the internuclear axis in the positions shown in Figure \(\PageIndex{1}\), rotating with equal probability in any plane containing the z-axis but unconstrained with respect to the angle \(\varphi\).

For the \(J = 1\), \(m_J = 1\) and \(m_J = -1\) states, the wavefunctions are given by
\[ \begin{align} Y^1_1 &= \sqrt {\frac {3}{8 \pi}} \sin \theta e^{i \varphi} \\[4pt] Y^{-1}_1 &= \sqrt {\frac {3}{8 \pi}} \sin \theta e^{-i \varphi} \label {7-44} \end{align}\]
The imaginary component in these wavefunctions is somewhat disconcerting until we realize that the modulus squared of the wavefunction has the physical interpretation of a probability density, and the imaginary component disappears in the modulus.
\[|Y^1_1|^2 = |Y^{-1}_1|^2 = \frac {3}{8 \pi} \sin ^2 \theta \label {7-45}\]
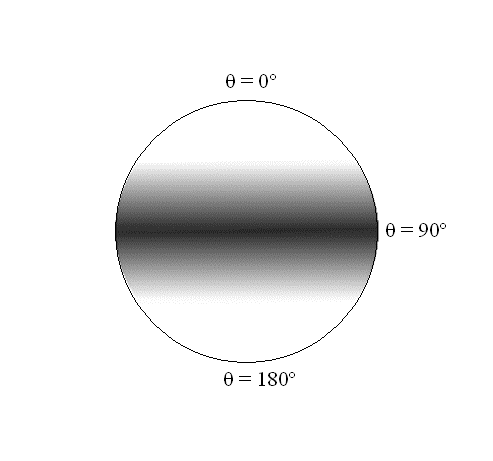
In these expressions, which are identical, the angle \(\varphi \) again does not appear. There are no constraints on the wavefunctions with respect to the angle \(\varphi\); i.e., the probability density is spread evenly over all values of \(\varphi \)associated with a particular \(\theta\). The \(\theta\) dependence is a \(\sin^2\) function, which has a maximum at 90º and goes to 0º as \(\theta\) goes to 0º and 180º for both of these rotational states as shown in Figure \(\PageIndex{3}\).
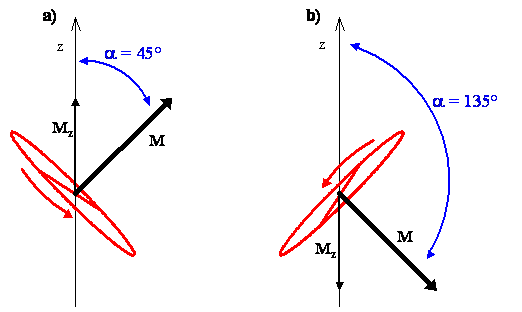
The classical interpretation of the rotation associated with the angular momentum vector for the \(m_J = 1\) state, which is tilted at an angle of 45º from the z-axis, says that the possible planes of rotation containing the internuclear axis of the molecule are aligned perpendicular to the angular momentum vector, as shown in Figure \(\PageIndex{4a}\). The molecule is rotating in any of these planes with equal probability.
For the \(m_J = -1\) state, the angular momentum vector is at an angle \(\alpha\) = 135º from the z-axis, and the possible planes of rotation containing the internuclear axis are perpendicular to it, as shown in Figure \(\PageIndex{4b}\). Using the right hand rule, the direction of rotation is clockwise for the \(m_J = -1\) state and counterclockwise for the \(m_J = 1\) state.
Exercise \(\PageIndex{19}\)
Five states have \(J = 2\). Calculate the angles the angular momentum vectors for these states make with respect to the z-axis. Sketch a diagram similar to Figure \(\PageIndex{4}\) in which all five angular momentum vectors for the \(J = 2\) energy level are placed on the same diagram. Describe how the molecule rotates relative to one of these vectors.


