6.5: Quantum Mechanical Tunneling
- Page ID
- 4509
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Quantum mechanical tunneling is a consequence of the fact that a vibrating molecule has a significant probability to be in the classically forbidden region of space, i.e. beyond the classical limit. Suppose that rather than having a harmonic potential for the displacement of an atom from its equilibrium position, one has a double well potential with a finite potential-energy barrier between the two sides as shown in Figure \(\PageIndex{1}\).
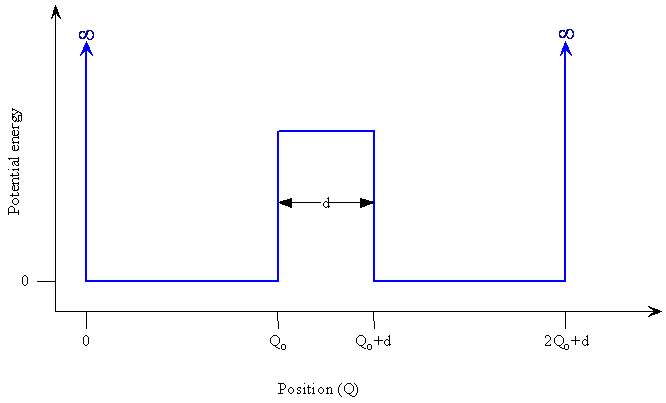
How might the wavefunctions for the position of the atom, or other particle such as an electron, with this type of potential look? A reasonable starting approximation would be to consider a harmonic oscillator wavefunction in each well. Because of their asymptotic approach to zero, the functions extend into the region of the barrier, i.e. into the classically forbidden region. These functions can even connect up with each other if the barrier is not too high or too wide. The connection of the two functions means that a particle starting out in the well on the left side has a finite probability of tunneling through the barrier and being found on the right side even though the energy of the particle is less than the barrier height. According to classical mechanics, the particle would be trapped on the left side if it did not have enough energy to go over the barrier. In quantum mechanics, the particle can tunnel through the barrier. An energy barrier does not necessarily restrict a quantum mechanical system to a certain region of space because the wavefunctions can penetrate through the barrier region. Tunneling has been proposed to explain electron transfer in some enzyme reactions and to account for mutations of DNA base pairs as a hydrogen atom in a hydrogen bond tunnels through the barrier from the electronegative atom of one base to the electronegative atom in the partner base.
What do we mean when we say that something like tunneling occurs quantum mechanically but not classically? We mean that classical mechanics is not an adequate description of the way the atomic world behaves. Classical mechanics works fine for macroscopic objects but not for nanoscopic objects. The importance of the mass and Planck's constant in determining whether an object can be described classically or not can be illustrated by the Uncertainty Principle. When the Uncertainty Principle,
\[\Delta x \Delta p > \frac {\hbar}{2},\]
and the relationship between momentum and wavelength,
\[p = \dfrac{h}{λ} \nonumber\]
was applied to macroscopic objects like a baseball. It was found that the uncertainties and wavelength are so small compared to macroscopic dimensions that the wave properties of these objects are not detectable. Large masses can be described classically because Planck's constant is so small. The situations examined in the following paragraphs consider tunneling along these same lines.
We first look at the case of a proton. Is it reasonable to think that a proton can tunnel through a potential barrier? Consider a hydrogen bond between two paired bases in a nucleic acid helix and the resulting double-well potential-energy function similar to the one illustrated in Figure \(\PageIndex{1}\).
Exercise \(\PageIndex{1}\)
Sketch potential-energy functions for each of the hydrogen bonds in a guanine-cytosine base pair. Describe how your drawings reflect the nature of the base pairing shown in standard biochemistry textbooks.
We want to compare \(Q_0\), the maximum classical displacement of the proton, with the separation of the potential wells, d, which we take as the width of the potential barrier at half its height. If d is much larger than \(Q_0\), tunneling would not be probable because the wavefunction, which falls off very rapidly (exponentially), would become extremely small, essentially zero within the barrier as Q increases beyond \(Q_0\). On the other hand, if d is not too much larger than \(Q_0\), then the wavefunction will still have a significant non-zero value at the further side of the barrier and tunneling will be probable.
The rate at which the wavefunction approaches zero in the barrier region depends upon both the height and width of the barrier. As the barrier height increases, the width must become smaller for tunneling to be significant, but we can still get a feeling for whether tunneling is reasonable or not by comparing the separation of the potential wells with \(Q_0\). For a hydrogen-bonded proton between two electronegative centers, d has been calculated to be approximately 0.1 nm (about 10% of a N-H bond length) and \(Q^2_0 = \frac {\hbar}{m \omega}\) giving \(Q_0\) = 0.01 nm. Since d is only 10 times larger than Q0 in this estimate, tunneling cannot be excluded as a real possibility.
Exercise \(\PageIndex{2}\)
Obtain a value for \(Q_0\) by using the mass of a proton and a characteristic vibrational frequency for a NH or OH bond (3300 cm-1).
Exercise \(\PageIndex{3}\)
Identify what happens to \(Q_0\), the ratio \(\frac {d}{Q_0}\), and your expectations for tunneling as the mass of the particle increases, e.g. if the proton were replaced by a deuteron.
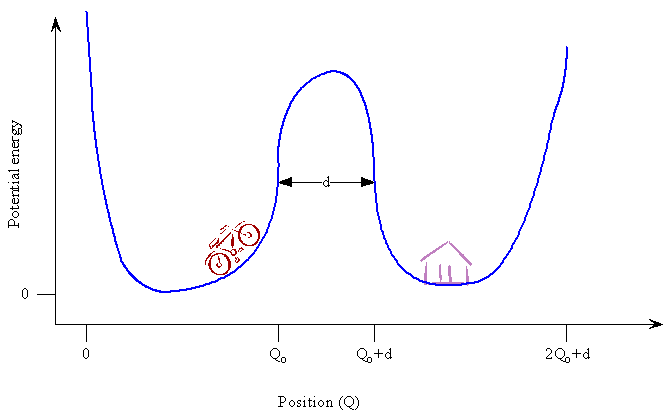
Now consider a macroscopic system for comparison. Assume that you and your bicycle are stuck in a valley one hill away from your home in the next valley. You are in your lowest energy state, and you have 1000 m to go. What conclusion do we reach if we apply the above estimates for the probability of tunneling to you? We want to use \(Q^2_0 \approx \frac {\hbar}{m \omega}\) to estimate your maximum displacement from the bottom of the valley and compare it to the distance to your home valley. For example, we can give you a mass of 100 kg and a frequency of oscillation between the two hills that form the valley of ω = 2π / 100 s. Your mass is 29 orders of magnitude (factors of ten) greater than that of a proton, and your oscillation frequency is 16 orders of magnitude smaller than that of a proton. This frequency means that it takes 100 s for you to complete one cycle rolling back and forth between the two hills that form the valley in which you are located. The larger mass dominates the smaller frequency with the result that your Q0 is 10-18 m, and the hill you need to cross is 1000 m wide, \(d \approx 10^3\) m. A bicyclist in the lowest energy quantum state has a maximum displacement of 10-18 nm (10-27 m) and a distance to tunnel of about 103 m. Tunneling under these conditions is not a probable event because the distance to go is so much larger than the maximum displacement. A bicyclist wouldn't have a chance in a lifetime of getting home without generating sufficient energy to ride over the hill. What would happen if Planck's constant were much larger? If h were 107 J s, then tunneling also would be important for massive objects like people, and it would make our lives easier and more interesting.
Exercise \(\PageIndex{4}\)
Verify that if h = 107 J s then tunneling would be important for people.


