6.1: Spatial Degrees of Freedom, Normal Coordinates and Normal Modes
- Page ID
- 4510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)To deal with the complexity of the vibrational motion in polyatomic molecules, we need to utilize the three important concepts listed as the title of this section. By a spatial degree of freedom, we mean an independent direction of motion. A single atom has three spatial degrees of freedom because it can move in three independent or orthogonal directions in space, i.e. along the x, y, or z-axes of a Cartesian coordinate system. Motion in any other direction results from combining velocity components along two or three of these directions. Two atoms have six spatial degrees of freedom because each atom can move in any of these three directions independently.
Equivalently, we also can say one atom has three spatial degrees of freedom because we need to specify the values of three coordinates \((x_1, y_1, z_1)\) to locate the atom. Two atoms have six spatial degrees of freedom because we need to specify the values of six coordinates, \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\), to locate two atoms in space. In general, to locate N atoms in space, we need to specify 3N coordinates, so a molecule comprised of N atoms has 3N spatial degrees of freedom.
Exercise \(\PageIndex{1}\)
Identify the number of spatial degrees of freedom for the following molecules: \(Cl_2\), \(CO_2\), \(H_2O\), \(CH_4\), \(C_2H_2\), \(C_2H_4\), \(C_6H_6\).
The motion of the atomic nuclei in a molecule is not as simple as translating each of the nuclei independently along the x, y, and z axes because the nuclei, which are positively charged, are coupled together by the electrostatic interactions with the electrons, which are negatively charged. The electrons between two nuclei effectively attract them to each other, forming a chemical bond.
Consider the case of a diatomic molecule, which has six degrees of freedom. The motion of the atoms is constrained by the bond. If one atom moves, a force will be exerted on the other atom because of the bond. The situation is like two balls coupled together by a spring. There are still six degrees of freedom, but the motion of atom 1 along x, y, and z is not independent of the motion of atom 2 along x, y, and z because the atoms are bound together.
It therefore is not very useful to use the six Cartesian coordinates, \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\), to describe the six degrees of freedom because the two atoms are coupled together. We need new coordinates that are independent of each other and yet account for the coupled motion of the two atoms. These new coordinates are called normal coordinates, and the motion described by a normal coordinate is called a normal mode.
A normal coordinate is a linear combination of Cartesian displacement coordinates. A linear combination is a sum of terms with constant weighting coefficients multiplying each term. The coefficients can be imaginary or any positive or negative number including +1 and -1. For example, the point or vector r = (1, 2, 3) in three-dimensional space can be written as a linear combination of unit vectors.
\[r = 1 \bar {x} + 2 \bar {y} + 3 \bar {z} \label {6-1}\]
A Cartesian displacement coordinate gives the displacement in a particular direction of an atom from its equilibrium position. The equilibrium positions of all the atoms are those points where no forces are acting on any of the atoms. Usually the displacements from equilibrium are considered to be small. For illustration, the Cartesian displacement coordinates for HCl are defined in Table \(\PageIndex{1}\), and they are illustrated in Figure \(\PageIndex{1}\).
Table 6. Cartesian displacement coordinates for HCl.*
\[q_1 = X_{H} - X^e_H\]
\[q_2 = y_{H} - y^e_H\]
\[q_3 = z_H - z^e_H\]
\[q_4 = x_{Cl} - x^e_{Cl}\]
\[q_5 = y_{Cl} - y^e_{Cl}\]
\[q_6 = z_{Cl} - z^e_{Cl}\]
*The superscript e designates the coordinate value at the equilibrium position.
Note that the position of one atom can be written as a vector \(r_1\) where \(r_1 = (x_1, y_1, z_1)\), and the positions of two atoms can be written as two vectors \(r_1\) and \(r_2\) or as a generalized vector that contains all six components \(r = (x_1, y_1, z_1, x_2, y_2, z_2)\). Similarly the six Cartesian displacement coordinates can be written as such a generalized vector \(q = (q_1, q_2, q_3, q_4, q_5, q_6)\).
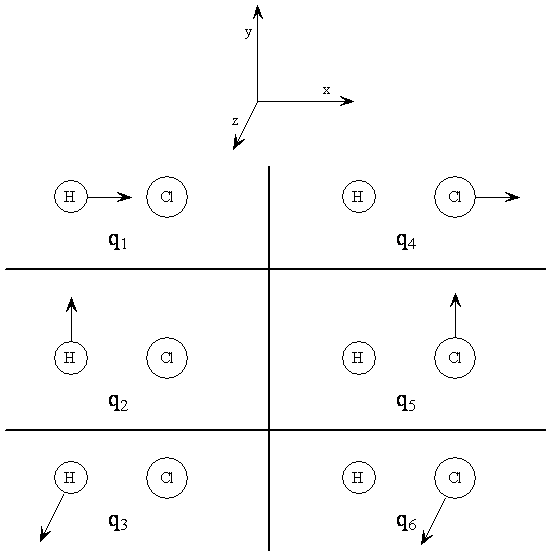
For a diatomic molecule it is easy to find the linear combinations of the Cartesian displacement coordinates that form the normal coordinates and describe the normal modes. Just take sums and differences of the Cartesian displacement coordinates. Refer to Table \(\PageIndex{1}\) and Figure \(\PageIndex{4}\). for the definition of the q's. The combination q1 + q4 corresponds to translation of the entire molecule in the x direction; call this normal coordinate Tx. Similarly we can define Ty = q2 + q5 and Tz = q3 + q6 as translations in the y and z directions, respectively. Now we have three normal coordinates that account for three of the degrees of freedom, the three translations of the entire molecule.
What do we do about the remaining three degrees of freedom? Here let's use a simple rule for doing creative science: if one thing works, try something similar and examine the result. In this case, if adding quantities works, try subtracting them. Examine the combination q2 - q5. This combination means that H is displaced in one direction and Cl is displaced in the opposite direction. Because of the bond, the two atoms cannot move completely apart, so this small displacement of each atom from equilibrium is the beginning of a rotation about the z-axis. Call this normal coordinate Rz. Similarly define Ry = q3 - q6 to be rotation about the y-axis. We now have found two rotational normal coordinates corresponding to two rotational degrees of freedom.
The remaining combination, q1 - q4, corresponds to the atoms moving toward each other along the x-axis. This motion is the beginning of a vibration, i.e. the oscillation of the atoms back and forth along the x-axis about their equilibrium positions, and accounts for the remaining sixth degree of freedom. We use Q for the vibrational normal coordinate.
\[Q = q_1 - q_4 \label {6-2}\]
To summarize: a normal coordinate is a linear combination of atomic Cartesian displacement coordinates that describes the coupled motion of all the atoms that comprise a molecule. A normal mode is the coupled motion of all the atoms described by a normal coordinate. While diatomic molecules have only one normal vibrational mode and hence one normal vibrational coordinate, polyatomic molecules have many.
Exercise \(\PageIndex{2}\)
Draw and label six diagrams, each similar to Figure \(\PageIndex{1}\), to show the 3 translational, 2 rotational and 1 vibrational normal coordinates of a diatomic molecule.
Exercise \(\PageIndex{3}\)
Vibrational normal modes have several distinguishing characteristics. Examine the animations for the normal modes of benzene shown in Figure \(\PageIndex{3}\) to identify and make a list of these characteristics. Use a molecular modeling program to calculate and visualize the normal modes of another molecule.
The list of distinguishing characteristics of normal modes that you compiled in Exercise \(\PageIndex{4}\) should include the following four properties. If not, reexamine the animations to confirm that these characteristics are present.
- In a particular vibrational normal mode, the atoms move about their equilibrium positions in a sinusoidal fashion with the same frequency.
- Each atom reaches its position of maximum displacement at the same time, but the direction of the displacement may differ for different atoms.
- Although the atoms are moving, the relationships among the relative positions of the different atoms do not change.
- The center of mass of the molecule does not move.
For the example of HCl, see Table \(\PageIndex{1}\), the first property, stated mathematically, means
\[q_1 = A_1 \sin (\omega t) \text {and} q_4 = A_4 \sin (\omega t) \label {6-3}\]
The maximum displacements or amplitudes are given by A1 and A4, and the frequency of oscillation (in radians per second) is ω for both displacement coordinates involved in the normal vibrational mode of HCl. Substitution of Equations (6-3) for the displacement coordinates into the expression determined above for the vibrational normal coordinate, Equation (6-2), yields
\[ Q = q_1 - q_4 = A_1 \sin (\omega t) - A_4 \sin (\omega t) \label {6-4}\]
This time-dependent expression describes the coupled motions of the hydrogen and chlorine atoms in a vibration of the HCl molecule. In general for a polyatomic molecule, the magnitude of each atom's displacement in a vibrational normal mode may be different, and some can be zero. If an amplitude, the A, for some atom in some direction is zero, it means that atom does not move in that direction in that normal mode. In different normal modes, the displacements of the atoms are different, and the frequencies of the motion generally are different. If two or more vibrational modes have the same vibrational frequency, these modes are called degenerate.
You probably noticed in Exercise \(\PageIndex{4}\) that the atoms reached extreme points in their motion at the same time but that they were not all moving in the same direction at the same time. These characteristics are described by the second and third properties from the list above. For the case of HCl, the two atoms always move in exactly opposite directions during the vibration. Mathematically, the negative sign in Equation that we developed for the normal coordinate, Q, accounts for this relationship.
This timing with respect to the direction of motion is called the phasing of the atoms. In a normal mode, the atoms move with a constant phase relationship to each other. The phase relationship is represented by a phase angle φ in the argument of the sine function that describes the time oscillation, sin(ωt + φ). The angle is called a phase angle because it shifts the sine function on the time axis. We can illustrate this phase relationship for HCl. Use the trigonometric identity
\[- \sin {\theta} = \sin (\theta + 180^0) \label {6-5}\]
in Equation \ref{6-4} to obtain
\[Q = A_1 \sin (\omega t ) + A_4 \sin (\omega t + 180^0) \label {6-6}\]
to see that that the phase angle for this case is 180o.
The phase angle \(\varphi\) accounts for the fact that the H atom and the Cl atom reach their maximum displacements in the positive x-direction, +A1 and +A4, at different times. Generally in a normal mode the phase angle \(\varphi\) is 0o or 180o. If \(\varphi\) = 0o for both atoms, the atoms move together, and they are said to be in-phase. For the vibration of a diatomic molecule such as HCl, the phase angle for one atom is \(\varphi\) = 0o, and the phase angle for the other atom is \(\varphi\) = 180o. The atoms therefore move in opposite directions any time, and the atoms are said to be 180o out-of-phase. When \(\varphi\) is 180o, two atoms reach the extreme points in their motion at the same time, but one is in the positive direction and the other is in the negative direction.
Phase relationships can be seen by watching a marching band. All the players are executing the same marching motion at the same frequency, but a few may be ahead or behind the rest. You might say, "They are out-of-step." You also could say, "They are out-of-phase."
To illustrate the fourth property for HCl, recall that the center of mass for a diatomic molecule is defined as the point where the following equation is satisfied.
\[m_H d_H = m_{Cl} d_{Cl} \label {6-7}\]
The masses of the atoms are given by \(m_H\) and \(m_Cl\), and \(d_H\) and \(d_{Cl}\) are the distances of these atoms from the center of mass.
Exercise \(\PageIndex{4}\)
Find the distances, dH and dCl, of the H and Cl atoms from the center of mass in HCl given that the bond length is 0.13 nm. In general for a diatomic molecule, AB, what determines the ratio dA/dB, and which atom moves the greater distance in the vibration?
In general, to satisfy the center of mass condition, a light atom is located further from the center of mass than a heavy atom. To keep the center of mass fixed during a vibration, the amplitude of motion of an atom must depend inversely on its mass. In other words, a light atom is located further from the center of mass and moves a longer distance in a vibration than a heavy atom.
Exercise \(\PageIndex{5}\)
Find the ratio of A1 to A4 from Equation that keeps the HCl center of mass stationary during a vibration. Find values for A1 and A4 that satisfy the condition
\[A12 + A42= 1.\]
Exercise \(\PageIndex{6}\)
For a vibrating HCl molecule, use the four properties of a normal vibrational mode, listed previously, to sketch a graph showing the position of the H atom (plot 1) and the position of the Cl atom (plot 2) as a function of time. Both plots should be on the same scale. Hint: place x on the vertical axis and time on the horizontal axis.
In general, a molecule with 3N spatial degrees of freedom has 3 translational normal modes (along each of the three axes), 3 rotational normal modes (around each of the three axes), and 3N-6 (the remaining number) different vibrational normal modes of motion. A linear molecule, as we have just seen, only has two rotational modes, so there are 3N-5 vibrational normal modes. Rotational motion about the internuclear axis in a linear molecule is not one of the 3N spatial degrees of freedom derived from the translation of atoms in three-dimensional space. Rather, such motion corresponds to other degrees of freedom, rotational motion of the electrons and a spinning motion of the nuclei. Indeed, the electronic wavefunction for a linear molecule is characterized by some angular momentum (rotation) about this axis, and nuclei have a property called spin.
Exercise \(\PageIndex{7}\)
Identify the number of translational, rotational, and vibrational normal modes for the following molecules: \(Cl_2, CO_2, H_2O, CH_4, C_2H_2, C_2H_4, C_2H_6, C_6H_6\). Using your intuition, draw diagrams similar to the ones in Exercise \(\PageIndex{3}\) to show the normal modes of \(H_2O\) and \(C_2H_4\). It is difficult to identify the normal modes of triatomic and larger molecules by intuition. A mathematical analysis is essential. It is easier to see the normal modes if you use a molecular modeling program like Spartan or Gaussian to generate and display the normal modes.
You probably found in trying to complete Exercise \(\PageIndex{7}\) that it is difficult to identify the normal modes and normal coordinates of triatomic and large molecules by intuition. A mathematical analysis is essential. A general analysis based on the Lagrangian formulation of classical mechanics is described separately.


