2.3: Photoelectric Effect
- Page ID
- 4474
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the photoelectric effect, light incident on the surface of a metal causes electrons to be ejected. The number of emitted electrons and their kinetic energy can be measured as a function of the intensity and frequency of the light. One might expect, as did the physicists at the beginning of the Twentieth Century, that the energy in the light wave (its intensity in \(J/m^2s\)) should be transferred to the kinetic energy of the emitted electrons. Also, the number of electrons that break away from the metal should change with the frequency of the light wave. This dependence on frequency was expected because the oscillating electric field of the light wave causes the electrons in the metal to oscillate back and forth, and the electrons in the metal respond at different frequencies. In other words, it was expected that the number of emitted electrons should depend upon the frequency, and their kinetic energy should depend upon the intensity of the light wave (at fixed wavelength).
The classical expectation of the photoelectric effect was that the number of emitted electrons would depend upon the frequency, and their kinetic energy should depend upon the intensity of the light wave.
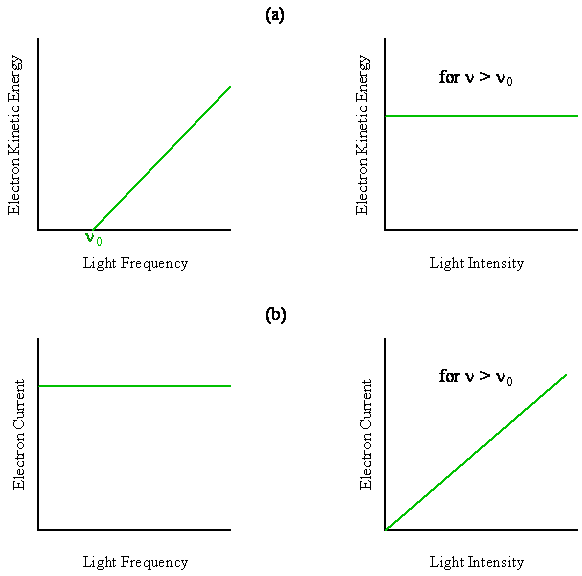
As shown in Figure \(\PageIndex{1}\), just the opposite behavior is observed in the photoelectric effect. The intensity affects the number of electrons, and the frequency affects the kinetic energy of the emitted electrons. From these sketches, we see that:
- the kinetic energy of the electrons is linearly proportional to the frequency of the incident radiation above a threshold value of \(ν_0\) (no current is observed below \(ν_0\)), and the kinetic energy is independent of the intensity of the radiation.
- the number of electrons (i.e. the electric current) is proportional to the light intensity (at a fixed wavelength) and independent of the frequency of the incident radiation above the threshold value of \(ν_0\) (no current is observed below \(ν_0\)).
In 1905, Albert Einstein explained the observations shown in Figure \(\PageIndex{1}\) with the bold hypothesis that energy carried by light existed in packets of an amount \(h\nu\). Each packet or photon could cause one electron to be ejected, which is like having a moving particle collide with and transfer energy to a stationary particle. The number of electrons ejected therefore depends upon the number of photons, i.e. the intensity of the light. Some of the energy in the packet is used to overcome the binding energy of the electron in the metal. This binding energy is called the work function, \(\Phi\). The remaining energy appears as the kinetic energy, \(\frac {1}{2} mv^2\), of the emitted electron.
Equations \(\ref{2-3}\) and \(\ref{2-4}\) express the conservation of energy for the photoelectric process
\[E_{photon} = K_{Eelectron} + W_{electron} \label {2-3}\]
\[h \nu = \frac {1}{2} mv^2 + \Phi \label {2-4}\]
Rearranging this equation reveals the linear dependence of kinetic energy on frequency as shown in Figure \(\PageIndex{1}\).
\[ \frac {1}{2} mv^2 = h \nu - \Phi \label {2-5}\]
The slope of the straight line obtained by plotting the kinetic energy as a function of frequency above the threshold frequency is just Planck’s constant, and the x-intercept, where \(\frac {1}{2} mv^2 = 0\), is just the work function of the metal, \(\Phi = hν_0\).
Example \(\PageIndex{1}\)
Sodium metal has a threshold frequency of \(4.40 × 10^{14}\) Hz. What is the kinetic energy of a photoelectron ejected from the surface of a piece of sodium when the ejecting photon is \(6.20 × 10^{14}\) Hz? What is the velocity of this photoelectron? From which region of the electromagnetic spectrum is this photon?
With such an analysis Einstein obtained a value for \(h\) in agreement with the value Planck deduced from the spectral distribution of black-body radiation. The fact that the same quantization constant could be derived from two very different experimental observations was very impressive and made the concept of energy quantization for both matter and light credible. In the next sections we will see that wavelength and momentum are properties that also are related for both matter and light.


