5.2: Orbital Symmetry

Symmetry provides additional quantum numbers or labels to use in describing the molecular orbitals. Each such quantum number further sub-divides the collection of all molecular orbitals into sets that have vanishing Hamiltonian matrix elements among members belonging to different sets.

Orbital interaction "topology" as discussed above plays a most- important role in determining the orbital energy level patterns of a molecule. Symmetry also comes into play, but in a different manner. Symmetry can be used to characterize the core, bonding, nonbonding, and antibonding molecular orbitals. Much of this chapter is devoted to how this can be carried out in a systematic manner. Once the various molecular orbitals have been labeled according to symmetry, it may be possible to recognize additional degeneracies that may not have been apparent on the basis of orbital-interaction considerations alone. Thus, topology provides the basic energy ordering pattern and then symmetry enters to identify additional degeneracies.

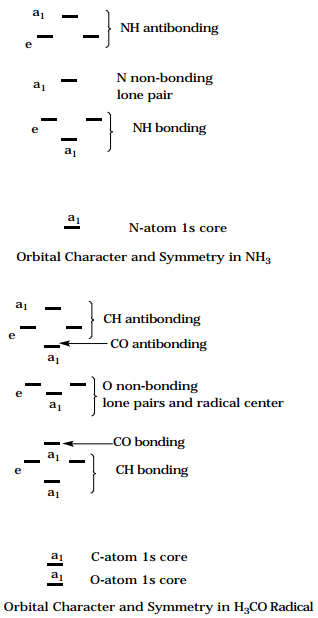
For example, the three NH bonding and three NH antibonding orbitals in \(NH_3\), when symmetry adapted within the \(C_{3v}\) point group, cluster into \(a_1\) and e molecular orbitals as shown in the Figure below. The N-atom localized non-bonding lone pair orbital and the N-atom 1s core orbital also belong to \(a_1\) symmetry.

In a second example, the three CH bonds, three CH antibonds, CO bond and antibond, and three O-atom non-bonding orbitals of the methoxy radical \(H_3C-O\) also cluster into \(a_1\) and e orbitals as shown below. In these cases, point group symmetry allows one to identify degeneracies that may not have been apparent from the structure of the orbital interactions alone.

Figure 5.2.1: Insert caption here!

The three resultant molecular orbital energies are, of course, identical to those obtained without symmetry above. The three LCAO-MO coefficients , now expressing the molecular orbitals in terms of the symmetry adapted orbitals are \(C_{is}\) = ( 0.707, 0.707, 0.0) for the bonding orbital, (0.0, 0.0, 1.00) for the nonbonding orbital, and (0.707, -0.707, 0.0) for the antibonding orbital. These coefficients, when combined with the symmetry adaptation coefficients \(C_{sa}\) given earlier, express the three molecular orbitals in terms of the three atomic orbitals as

\[\phi_i= \sum \limits_{sa} C_{is} C_{sa} \chi_a \nonumber \]

The sum

\[\sum \limits_s C_{is}C_{sa} \nonumber \]

gives the LCAO-MO coefficients \(C_{ia}\) which, for example, for the bonding orbital, are \(( 0.707^2, 0.707, 0.707^2)\), in agreement with what was found earlier without using symmetry.

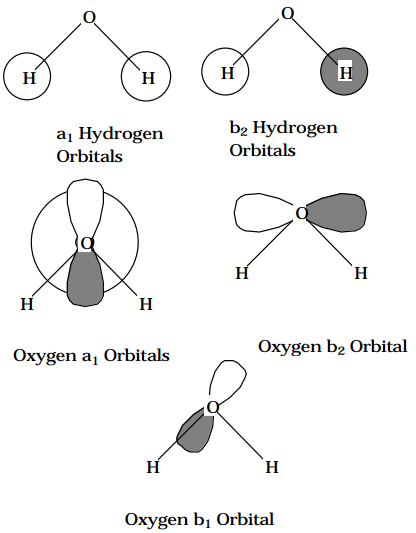
The low energy orbitals of the \(H_2O\) molecule can be used to illustrate the use of symmetry within the primitive ao basis as well as in terms of hybrid orbitals. The 1s orbital on the Oxygen atom is clearly a nonbonding core orbital. The Oxygen 2s orbital and its three 2p orbitals are of valence type, as are the two Hydrogen 1s orbitals. In the absence of symmetry, these six valence orbitals would give rise to a 6x6 secular problem. By combining the two Hydrogen 1s orbitals into 0.707(\(1s_L + 1s_R\)) and 0.707(\(1s_L - 1s_R\)) symmetry adapted orbitals (labeled \(a_1 \text{ and } b_2 \text{ within the } C_{2v}\) point group; see the Figure below), and recognizing that the Oxygen 2s and \(2p_z\) orbitals belong to \(a_1\) symmetry (the z axis is taken as the \(C_2\) rotation axis and the x axis is taken to be perpendicular to the plane in which the three nuclei lie) while the \(2p_x\) orbital is \(b_1\) and the \(2p_y\) orbital is \(b_2\), allows the 6x6 problem to be decomposed into a 3x3 ( \(a_1\)) secular problem, a 2x2 ( \(b_2\)) secular problem and a 1x1 ( \(b_1\) ) problem. These decompositions allow one to conclude that there is one nonbonding \(b_1\) orbital (the Oxygen \(2p_x\) orbital), bonding and antibonding \(b_2\) orbitals ( the O-H bond and antibond formed by the Oxygen \(2p_y\) orbital interacting with 0.707(\(1s_L - 1s_R\))), and, finally, a set of bonding, nonbonding, and antibonding \(a_1\) orbitals (the O-H bond and antibond formed by the Oxygen 2s and \(2p_z\) orbitals interacting with 0.707(\(1s_L + 1s_R\)) and the nonbonding orbital formed by the Oxygen 2s and \(2p_z\) orbitals combining to form the "lone pair" orbital directed along the z-axis away from the two Hydrogen atoms).

Figure 5.2.2: Insert caption here!

Alternatively, to analyze the \(H_2O\) molecule in terms of hybrid orbitals, one first combines the Oxygen 2s, \(2p_z, 2p_x and 2p_y\) orbitals to form four \(sp^3\) hybrid orbitals. The valence-shell electron-pair repulsion (VSEPR) model of chemical bonding (see R. J. Gillespie and R. S. Nyholm, Quart. Rev. 11, 339 (1957) and R. J. Gillespie, J. Chem. Educ. 40, 295 (1963)) directs one to involve all of the Oxygen valence orbitals in the hybridization because four \(\sigma\)-bond or nonbonding electron pairs need to be accommodated about the Oxygen center; no \(\pi\) orbital interactions are involved, of course. Having formed the four \(sp^3\) hybrid orbitals, one proceeds as with the primitive atomic orbitals; one forms symmetry adapted orbitals. In this case, the two Hydrogen 1s orbitals are combined exactly as above to form

\[0.707(1s_L + 1s_R) \nonumber \]

and

\[0.707(1s_L - 1s_R). \nonumber \]

The two \(sp^3\) hybrids which lie in the plane of the H and O nuclei ( label them L and R) are combined to give symmetry adapted hybrids: 0.707(L+R) and 0.707(L-R), which are of \(a_1 \text{ and } b_2\) symmetry, respectively (Figure Figure 5.2.3). The two \(sp^3\) hybrids that lie above and below the plane of the three nuclei (label them T and B) are also symmetry adapted to form 0.707(T+ B) and 0.707(TB), which are of \(a_1 \text{ and } b_1\) symmetry, respectively. Once again, one has broken the 6x6 secular problem into a 3x3 \(a_1\) block, a 2x2 \(b_2\) block and a 1x1 \(b_1\) block. Although the resulting bonding, nonbonding and antibonding \(a_1\) orbitals, the bonding and antibonding \(b_2\) orbitals and the nonbonding \(b_1\) orbital are now viewed as formed from symmetry adapted Hydrogen orbitals and four Oxygen \(sp^3\) orbitals, they are, of course, exactly the same molecular orbitals as were obtained earlier in terms of the symmetry adapted primitive aos. The formation of hybrid orbitals was an intermediate step which could not alter the final outcome.

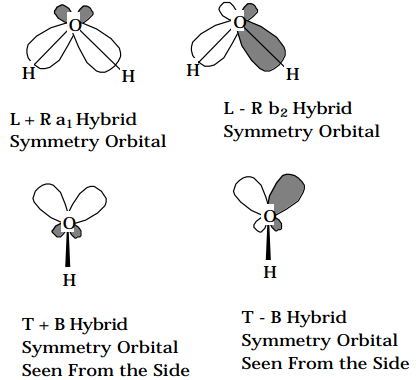
Figure 5.2.3: Insert caption here!

That no degenerate molecular orbitals arose in the above examples is a result of the fact that the \(C_{2v}\) point group to which \(H_2O\) and the allyl system belong (and certainly the \(C_s\) subgroup which was used above in the allyl case) has no degenerate representations. Molecules with higher symmetry such as \(NH_3 , CH_4\), and benzene have energetically degenerate orbitals because their molecular point groups have degenerate representations.