5.1: Orbital Interaction Topology
- Page ID
- 60551
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
The orbital interactions determine how many and which molecular orbitals will have low (bonding), intermediate (non-bonding), and higher (antibonding) energies, with all energies viewed relative to those of the constituent atomic orbitals. The general patterns that are observed in most compounds can be summarized as follows:
- If the energy splittings among a given atom's atomic orbitals with the same principal quantum number are small, hybridization can easily occur to produce hybrid orbitals that are directed toward (and perhaps away from) the other atoms in the molecule. In the first-row elements (Li, Be, B, C, N, O, and F), the 2s-2p splitting is small, so hybridization is common. In contrast, for Ca, Ga, Ge, As, and Br it is less common, because the 4s-4p splitting is larger. Orbitals directed toward other atoms can form bonding and antibonding mos; those directed toward no other atoms will form nonbonding molecular orbitals.
- In attempting to gain a qualitative picture of the electronic structure of any given molecule, it is advantageous to begin by hybridizing the atomic orbitals of those atoms which contain more than one ao in their valence shell. Only those atomic orbitals that are not involved in p-orbital interactions should be so hybridized.
- Atomic or hybrid orbitals that are not directed in a s-interaction manner toward other atomic orbitals or hybrids on neighboring atoms can be involved in p-interactions or in nonbonding interactions.
- Pairs of atomic orbitals or hybrid orbitals on neighboring atoms directed toward one another interact to produce bonding and antibonding orbitals. The more the bonding orbital lies below the lower-energy ao or hybrid orbital involved in its formation, the higher the antibonding orbital lies above the higher-energy ao or hybrid orbital.
For example, in formaldehyde, \(H_2CO\), one forms \(sp^2\) hybrids on the C atom; on the O atom, either sp hybrids (with one p orbital "reserved" for use in forming the \(\pi \text{ and } \pi^{\text{*}}\) orbitals and another p orbital to be used as a non-bonding orbital lying in the plane of the molecule) or \(sp^2\) hybrids (with the remaining p orbital reserved for the \(\pi \text{ and } \pi^{\text{*}}\) orbitals) can be used. The H atoms use their 1s orbitals since hybridization is not feasible for them. The C atom clearly uses its \(sp^2\) hybrids to form two CH and one CO \(\sigma\) bonding - antibonding orbital pairs.
The O atom uses one of its sp or \(sp^2\) hybrids to form the CO \(\sigma\) bond and antibond. When sp hybrids are used in conceptualizing the bonding, the other sp hybrid forms a lone pair orbital directed away from the CO bond axis; one of the atomic p orbitals is involved in the CO \(\pi \text{ and } \pi^{\text{*}}\) orbitals, while the other forms an in-plane non-bonding orbital. Alternatively, when \(sp^2\) hybrids are used, the two \(sp^2\) hybrids that do not interact with the C-atom \(sp^2\) orbital form the two non-bonding orbitals. Hence, the final picture of bonding, non-bonding, and antibonding orbitals does not depend on which hybrids one uses as intermediates.
As another example, the 2s and 2p orbitals on the two N atoms of \(N_2\) can be formed into pairs of sp hybrids on each N atom plus a pair of \(p_{\pi}\) atomic orbitals on each N atom. The sp hybrids directed toward the other N atom give rise to bonding \(\sigma \text{ and antibonding } \sigma^{\text{*}}\) orbitals, and the sp hybrids directed away from the other N atom yield nonbonding \(\sigma\) orbitals. The p\(_\pi\) orbitals, which consist of 2p orbitals on the N atoms directed perpendicular to the N-N bond axis, produce bonding \(\pi \text{ and antibonding } \pi^{\text{*}}\) orbitals. - In general, \(\sigma\) interactions for a given pair of atoms interacting are stronger than \(\pi\) interactions (which, in turn, are stronger than \(\delta\) interactions, etc.) for any given sets (i.e., principal quantum number) of atomic orbitals that interact. Hence, \(\sigma\) bonding orbitals (originating from a given set of aos) lie below \(\pi\) bonding orbitals, and \(\sigma^{\text{*}}\) orbitals lie above \(\pi^{\text{*}}\) orbitals that arise from the same sets of aos. In the \(N_2\) example, the \(\sigma\) bonding orbital formed from the two sp hybrids lies below the \(\pi\) bonding orbital, but the \(\pi^{\text{*}}\) orbital lies below the \(\sigma^{\text{*}}\) orbital. In the \(H_2CO\) example, the two CH and the one CO bonding orbitals have low energy; the CO \(\pi\) bonding orbital has the next lowest energy; the two O-atom non-bonding orbitals have intermediate energy; the CO \(\pi^{\text{*}}\) orbital has somewhat higher energy; and the two CH and one CO antibonding orbitals have the highest energies.
- If a given ao or hybrid orbital interacts with or is coupled to orbitals on more than a single neighboring atom, multicenter bonding can occur. For example, in the allyl radical the central carbon atom's \(p_\pi\) orbital is coupled to the \(p_\pi\) orbitals on both neighboring atoms; in linear \(Li_3\), the central Li atom's 2s orbital interacts with the 2s orbitals on both terminal Li atoms; in triangular \(Cu_3\), the 2s orbitals on each Cu atom couple to each of the other two atoms' 4s orbitals.
- Multicenter bonding that involves "linear" chains containing N atoms (e.g., as in conjugated polyenes or in chains of Cu or Na atoms for which the valence orbitals on one atom interact with those of its neighbors on both sides) gives rise to mo energy patterns in which there are N/2 (if N is even) or \(N/2 -1\) non-degenerate bonding orbitals and the same number of antibonding orbitals (if N is odd, there is also a single non-bonding orbital).
- Multicenter bonding that involves "cyclic" chains of N atoms (e.g., as in cyclic conjugated polyenes or in rings of Cu or Na atoms for which the valence orbitals on one atom interact with those of its neighbors on both sides and the entire net forms a closed cycle) gives rise to mo energy patterns in which there is a lowest non-degenerate orbital and then a progression of doubly degenerate orbitals. If N is odd, this progression includes (N- 1)/2 levels; if N is even, there are (N-2)/2 doubly degenerate levels and a final nondegenerate highest orbital. These patterns and those that appear in linear multicenter bonding are summarized in the Figures shown below.
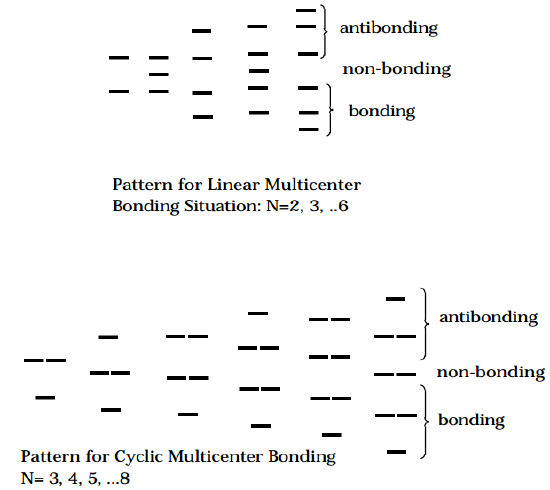
Figure 5.1.1: Insert caption here!
- In extended systems such as solids, atom-based orbitals combine as above to form so called 'bands' of molecular orbitals. These bands are continuous rather than discrete as in the above cases involving small polyenes. The energy 'spread' within a band depends on the overlap among the atom-based orbitals that form the band; large overlap gives rise to a large band width, while small overlap produces a narrow band. As one moves from the bottom (i.e., the lower energy part) of a band to the top, the number of nodes in the corresponding band orbital increases, as a result of which its bonding nature decreases. In the figure shown below, the bands of a metal such as Ni (with 3d, 4s, and 4p orbitals) is illustrated. The d-orbital band is narrow because the 3d orbitals are small and hence do not overlap appreciably; the 4s and 4p bands are wider because the larger 4s and 4p orbitals overlap to a greater extent. The d-band is split into \(\sigma, \pi, and \delta\) components corresponding to the nature of the overlap interactions among the constituent atomic d orbitals. Likewise, the p-band is split into \(\sigma \text{ and } \pi\) components. The widths of the \(\sigma\) components of each band are larger than those of the \(\pi\) components because the corresponding \(\sigma\) overlap interactions are stronger. The intensities of the bands at energy E measure the densities of states at that E. The total integrated intensity under a given band is a measure of the total number of atomic orbitals that form the band.
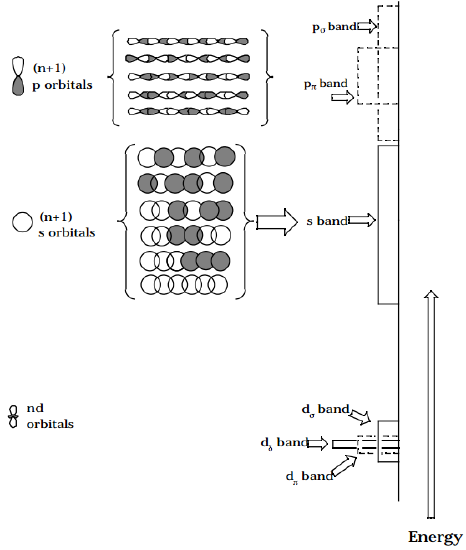
Figure 5.1.2: Insert caption here!


