13.3: The Determinant as a Volume
- Page ID
- 106884
Before discussing the properties of determinants, it will be useful to note that a determinant represents the volume of a box.
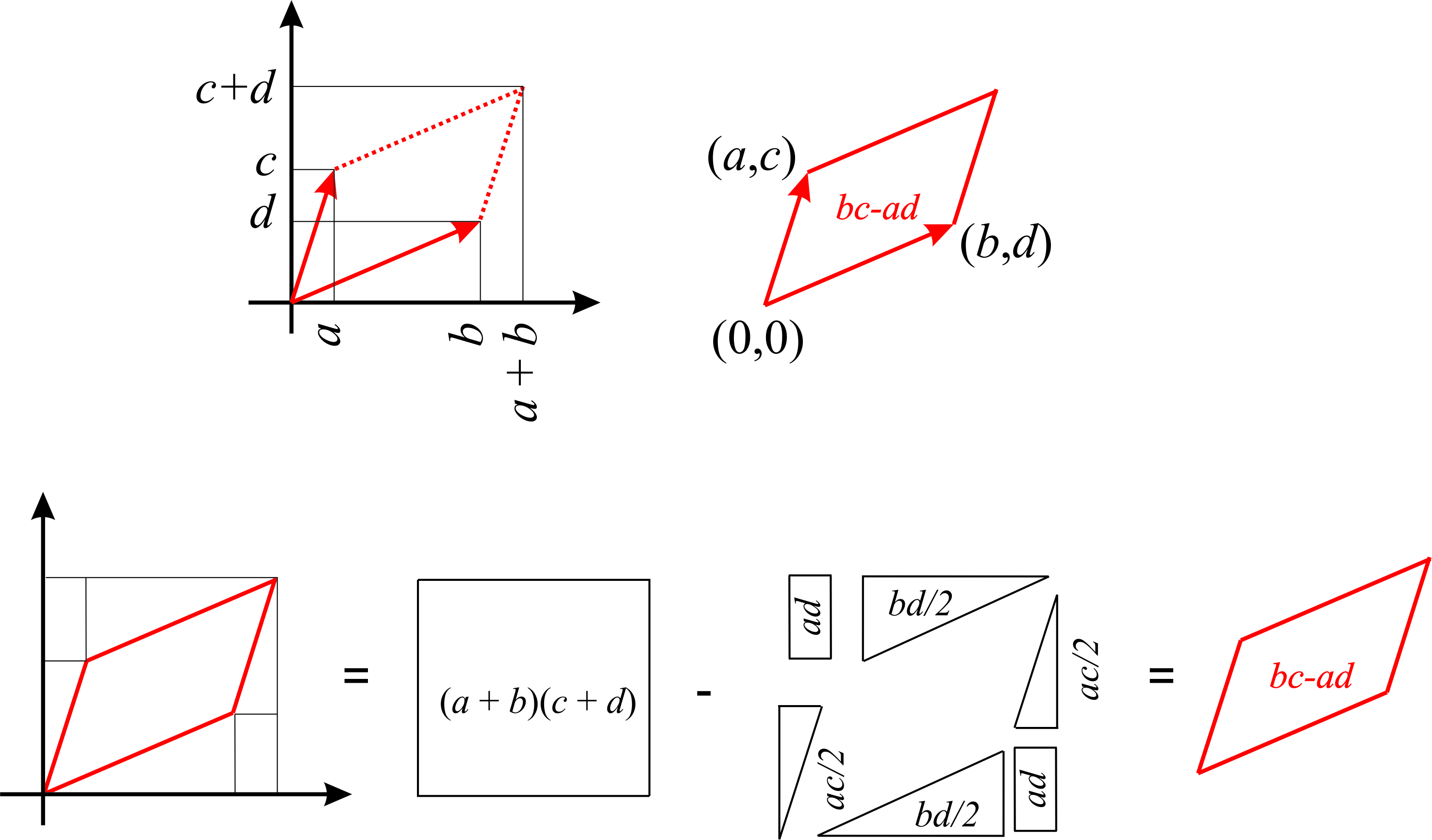
In two dimensions, the absolute value of a \(2\times 2\) determinant represents the area of the parallelogram whose sides are the two columns (or rows) of the determinant. Suppose you have two vectors: \(\vec{v_1}=(b,d)\) and \(\vec{v_2}=(a,c)\) (see Figure \(\PageIndex{2}\)). The area of the parallelogram constructed with these two vectors as sides is the absolute value of the determinant whose columns are \(\vec{v_1}\) and \(\vec{v_2}\):
\[A= \begin{vmatrix} b&a\\ d&c \end{vmatrix} \nonumber\]
A geometrical proof of this statement is shown in Figure \(\PageIndex{1}\). The sign of the determinant is related to the orientation of the parallelogram. If you extend your right hand, and use your thumb and index finger to represent the two vectors, the determinant will be positive if the vector along your thumb is in the first column and the vector and your index finger is in the second column, and will be negative if it is the other way around (Figure \(\PageIndex{2}\)).
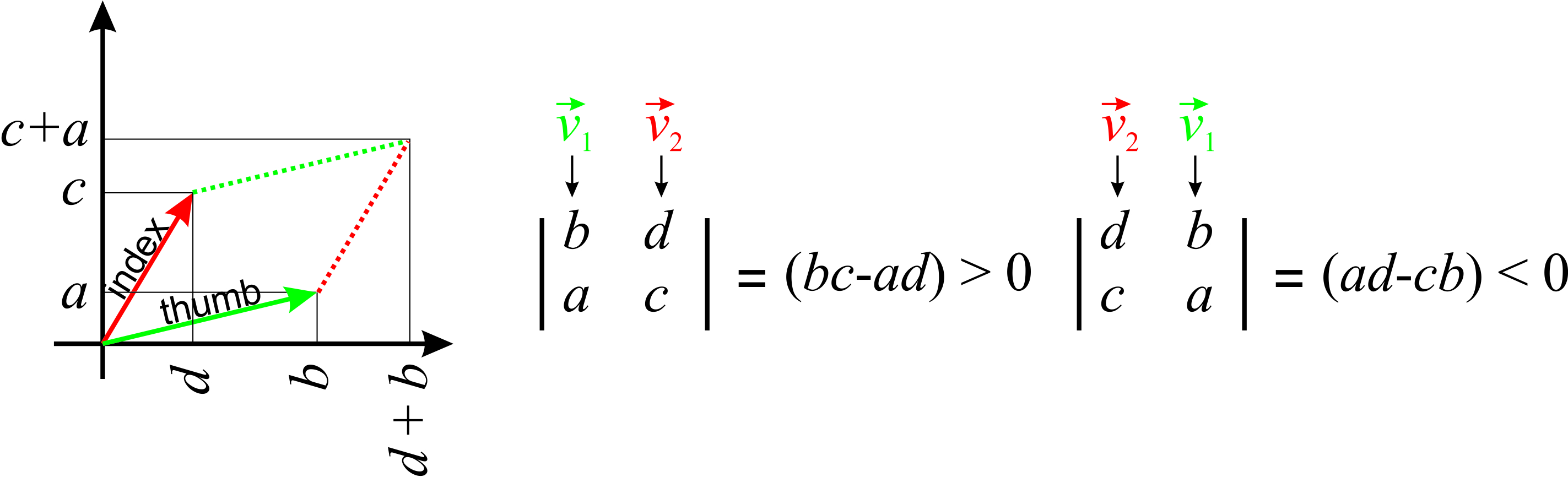
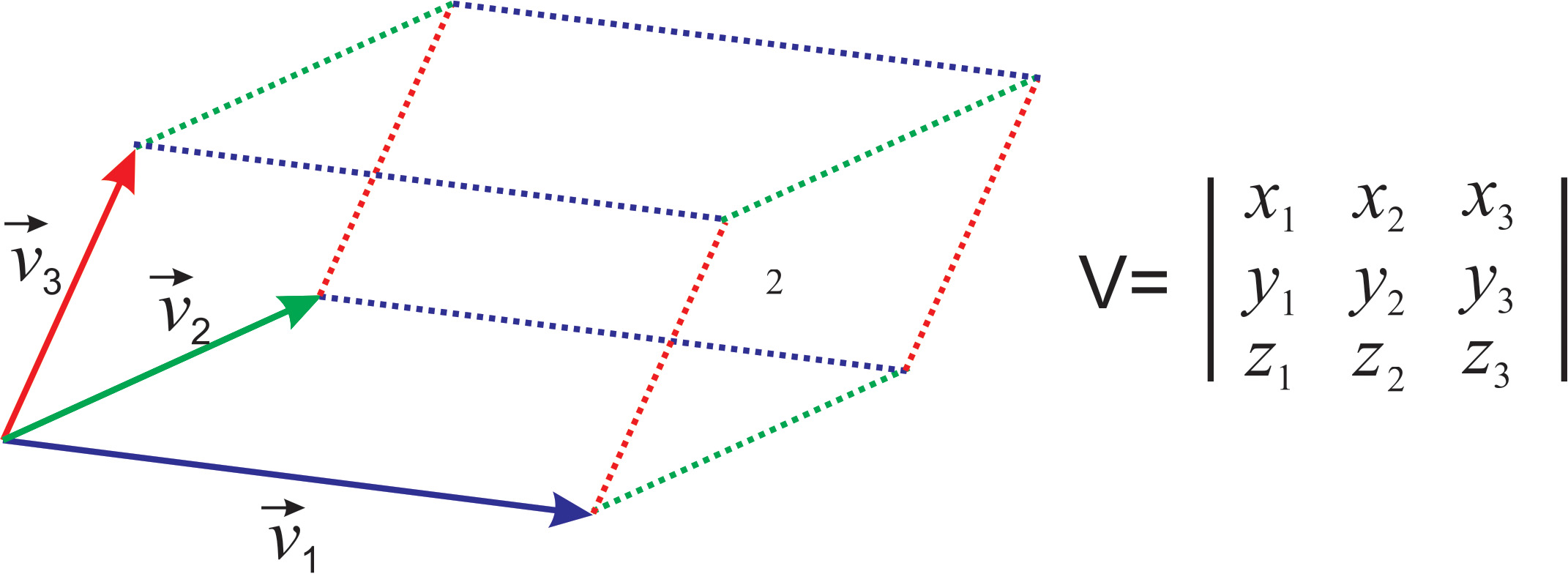
For a \(3\times 3\) determinant, its absolute value represents the volume of the parallelepiped (“the box”) whose edges are the vectors that are the columns of the determinant (Figure \(\PageIndex{3}\))
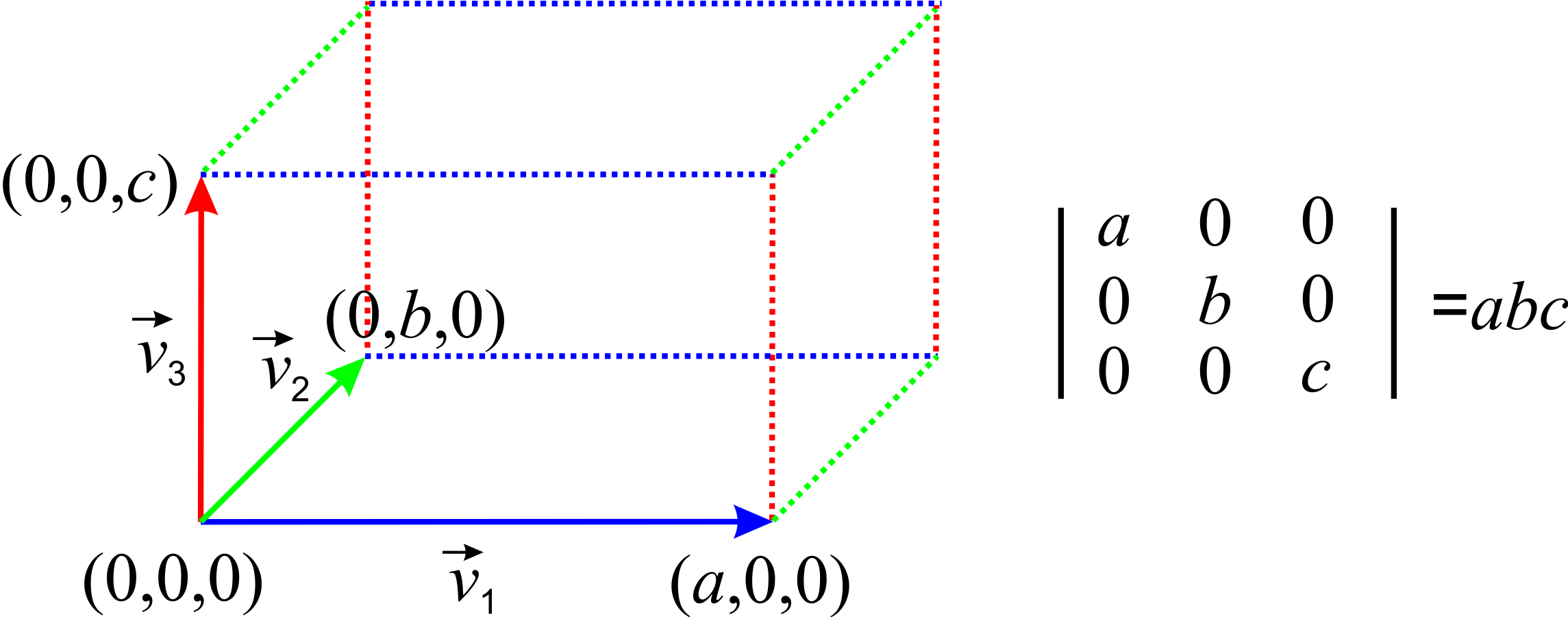
This notion will help us understand and remember some useful properties of determinants. For example, we can readily conclude that a determinant that contains non-zero entries only in the main diagonal (top left to bottom right) is the product of the diagonal entries:
\[\begin{vmatrix} a &0&0 \\ 0&b &0 \\ 0& 0 &c \end{vmatrix}=abc \nonumber\]
This is true because the columns represent vectors that are aligned with the \(x\), \(y\) and \(z\) axes respectively, so the volume of the resulting box is the product of the dimensions along \(x\), \(y\) and \(z\) (Figure \(\PageIndex{4}\)):