10.2: Area and Volume Elements
- Page ID
- 106863
In any coordinate system it is useful to define a differential area and a differential volume element. In cartesian coordinates the differential area element is simply \(dA=dx\;dy\) (Figure \(\PageIndex{1}\)), and the volume element is simply \(dV=dx\;dy\;dz\).
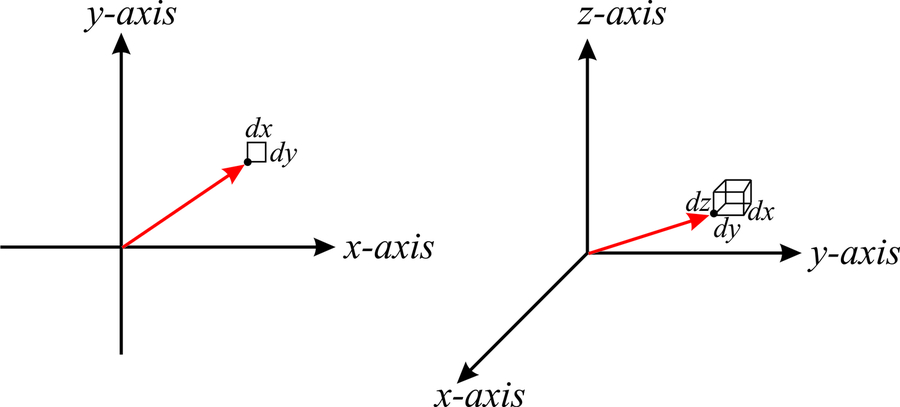
We already performed double and triple integrals in cartesian coordinates, and used the area and volume elements without paying any special attention. For example, in example [c2v:c2vex1], we were required to integrate the function \({\left | \psi (x,y,z) \right |}^2\) over all space, and without thinking too much we used the volume element \(dx\;dy\;dz\) (see page ). We also knew that “all space” meant \(-\infty\leq x\leq \infty\), \(-\infty\leq y\leq \infty\) and \(-\infty\leq z\leq \infty\), and therefore we wrote:
\[\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }{\left | \psi (x,y,z) \right |}^2\; dx \;dy \;dz=1 \nonumber\]
But what if we had to integrate a function that is expressed in spherical coordinates? Would we just replace \(dx\;dy\;dz\) by \(dr\; d\theta\; d\phi\)? The answer is no, because the volume element in spherical coordinates depends also on the actual position of the point. This will make more sense in a minute. Coming back to coordinates in two dimensions, it is intuitive to understand why the area element in cartesian coordinates is \(dA=dx\;dy\) independently of the values of \(x\) and \(y\). This is shown in the left side of Figure \(\PageIndex{2}\). However, in polar coordinates, we see that the areas of the gray sections, which are both constructed by increasing \(r\) by \(dr\), and by increasing \(\theta\) by \(d\theta\), depend on the actual value of \(r\). Notice that the area highlighted in gray increases as we move away from the origin.
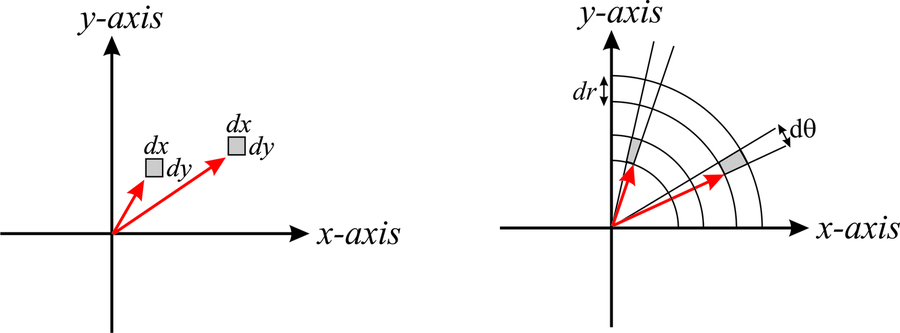
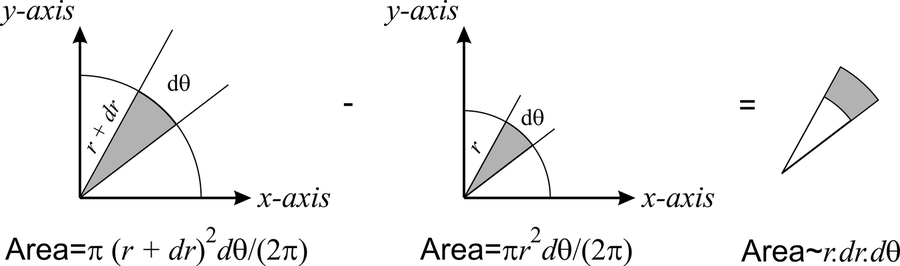
The area shown in gray can be calculated from geometrical arguments as
\[dA=\left[\pi (r+dr)^2- \pi r^2\right]\dfrac{d\theta}{2\pi}.\]
Because \(dr<<0\), we can neglect the term \((dr)^2\), and \(dA= r\; dr\;d\theta\) (see Figure \(10.2.3\)).
Let’s see how this affects a double integral with an example from quantum mechanics. The wave function of the ground state of a two dimensional harmonic oscillator is: \(\psi(x,y)=A e^{-a(x^2+y^2)}\). We know that the quantity \(|\psi|^2\) represents a probability density, and as such, needs to be normalized:
\[\int\limits_{all\;space} |\psi|^2\;dA=1 \nonumber\]
This statement is true regardless of whether the function is expressed in polar or cartesian coordinates. However, the limits of integration, and the expression used for \(dA\), will depend on the coordinate system used in the integration.
In cartesian coordinates, “all space” means \(-\infty<x<\infty\) and \(-\infty<y<\infty\). The differential of area is \(dA=dxdy\):
\[\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty} A^2e^{-2a(x^2+y^2)}\;dxdy=1 \nonumber\]
In polar coordinates, “all space” means \(0<r<\infty\) and \(0<\theta<2\pi\). The differential of area is \(dA=r\;drd\theta\). The function \(\psi(x,y)=A e^{-a(x^2+y^2)}\) can be expressed in polar coordinates as: \(\psi(r,\theta)=A e^{-ar^2}\)
\[\int\limits_{all\;space} |\psi|^2\;dA=\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=1 \nonumber\]
Both versions of the double integral are equivalent, and both can be solved to find the value of the normalization constant (\(A\)) that makes the double integral equal to 1. In polar coordinates:
\[\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi} A^2 e^{-2ar^2}r\;d\theta dr=A^2\int\limits_{0}^{\infty}e^{-2ar^2}r\;dr\int\limits_{0}^{2\pi}\;d\theta =A^2\times\dfrac{1}{4a}\times2\pi=1 \nonumber\]
Therefore1, \(A=\sqrt{2a/\pi}\). The same value is of course obtained by integrating in cartesian coordinates.
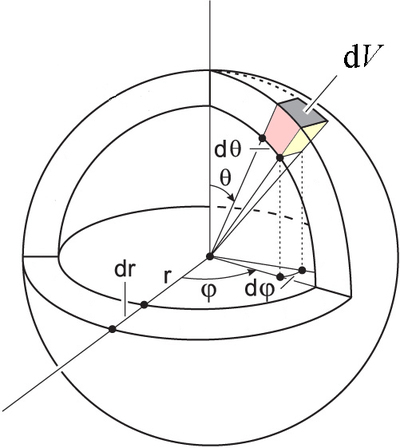
It is now time to turn our attention to triple integrals in spherical coordinates. In cartesian coordinates, the differential volume element is simply \(dV= dx\,dy\,dz\), regardless of the values of \(x, y\) and \(z\). Using the same arguments we used for polar coordinates in the plane, we will see that the differential of volume in spherical coordinates is not \(dV=dr\,d\theta\,d\phi\). The geometrical derivation of the volume is a little bit more complicated, but from Figure \(\PageIndex{4}\) you should be able to see that \(dV\) depends on \(r\) and \(\theta\), but not on \(\phi\). The volume of the shaded region is
\[\label{eq:dv} dV=r^2\sin\theta\,d\theta\,d\phi\,dr\]
We will exemplify the use of triple integrals in spherical coordinates with some problems from quantum mechanics. We already introduced the Schrödinger equation, and even solved it for a simple system in Section 5.4. We also mentioned that spherical coordinates are the obvious choice when writing this and other equations for systems such as atoms, which are symmetric around a point.
As we saw in the case of the particle in the box (Section 5.4), the solution of the Schrödinger equation has an arbitrary multiplicative constant. Because of the probabilistic interpretation of wave functions, we determine this constant by normalization. The same situation arises in three dimensions when we solve the Schrödinger equation to obtain the expressions that describe the possible states of the electron in the hydrogen atom (i.e. the orbitals of the atom). The Schrödinger equation is a partial differential equation in three dimensions, and the solutions will be wave functions that are functions of \(r, \theta\) and \(\phi\). The lowest energy state, which in chemistry we call the 1s orbital, turns out to be:
\[\psi_{1s}=Ae^{-r/a_0} \nonumber\]
This particular orbital depends on \(r\) only, which should not surprise a chemist given that the electron density in all \(s\)-orbitals is spherically symmetric. We will see that \(p\) and \(d\) orbitals depend on the angles as well. Regardless of the orbital, and the coordinate system, the normalization condition states that:
\[\int\limits_{all\;space} |\psi|^2\;dV=1 \nonumber\]
For a wave function expressed in cartesian coordinates,
\[\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\psi^*(x,y,z)\psi(x,y,z)\,dxdydz \nonumber\]
where we used the fact that \(|\psi|^2=\psi^* \psi\).
In spherical coordinates, “all space” means \(0\leq r\leq \infty\), \(0\leq \phi\leq 2\pi\) and \(0\leq \theta\leq \pi\). The differential \(dV\) is \(dV=r^2\sin\theta\,d\theta\,d\phi\,dr\), so
\[\int\limits_{all\;space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]
Let’s see how we can normalize orbitals using triple integrals in spherical coordinates.
When solving the Schrödinger equation for the hydrogen atom, we obtain \(\psi_{1s}=Ae^{-r/a_0}\), where \(A\) is an arbitrary constant that needs to be determined by normalization. Find \(A\).
Solution
In spherical coordinates,
\[\int\limits_{all\; space} |\psi|^2\;dV=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]
because this orbital is a real function, \(\psi^*(r,\theta,\phi)\psi(r,\theta,\phi)=\psi^2(r,\theta,\phi)\). In this case, \(\psi^2(r,\theta,\phi)=A^2e^{-2r/a_0}\).
Therefore,
\[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}\psi^*(r,\theta,\phi)\psi(r,\theta,\phi) \, r^2 \sin\theta \, dr d\theta d\phi=\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=1 \nonumber\]
\[\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\int\limits_{0}^{\infty}A^2e^{-2r/a_0}\,r^2\sin\theta\,dr d\theta d\phi=A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr \nonumber\]
The result is a product of three integrals in one variable:
\[\int\limits_{0}^{2\pi}d\phi=2\pi \nonumber\]
\[\int\limits_{0}^{\pi}\sin\theta \;d\theta=-\cos\theta|_{0}^{\pi}=2 \nonumber\]
\[\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=? \nonumber\]
From the formula sheet:
\[\int_{0}^{\infty}x^ne^{-ax}dx=\dfrac{n!}{a^{n+1}}, \nonumber\]
where \(a>0\) and \(n\) is a positive integer.
In this case, \(n=2\) and \(a=2/a_0\), so:
\[\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=\dfrac{2!}{(2/a_0)^3}=\dfrac{2}{8/a_0^3}=\dfrac{a_0^3}{4} \nonumber\]
Putting the three pieces together:
\[A^2\int\limits_{0}^{2\pi}d\phi\int\limits_{0}^{\pi}\sin\theta \;d\theta\int\limits_{0}^{\infty}e^{-2r/a_0}\,r^2\;dr=A^2\times2\pi\times2\times \dfrac{a_0^3}{4}=1 \nonumber\]
\[A^2\times \pi \times a_0^3=1\rightarrow A=\dfrac{1}{\sqrt{\pi a_0^3}} \nonumber\]
The normalized 1s orbital is, therefore:
\[\displaystyle{\color{Maroon}\dfrac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}} \nonumber\]


