1.3: The Exponential Function
- Page ID
- 106800
In Section 1.1 you were asked to review some properties of the exponential function. Here, we will learn (or review) how to sketch exponential functions with negative exponents quickly. These types of functions appear very often in chemistry, so it is important that you know how to visualize them without the help of a computer or calculator.
Suppose we want to sketch the function \(y = ae^{−kx}\), where \(a\) and \(k\) are positive real numbers (e.g. \(y = 3e^{−2x}\)). We could consider negative values of the variable \(x\), but often \(x\) represents a time or another variable for which only positive values make sense, so we will consider values of \(x \geq 0\).
First, let’s find out the value of \(y(0)\), where the function crosses the \(y\)−axis. Because \(e^0 = 1\), \(y(0) = a\). The number \(a\) is often called “the pre-exponential factor” (i.e. the factor before the exponential), or the “amplitude” of the function. This is the amplitude because it will be the highest point in our plot.
Now, let’s see what happens as \(x \rightarrow \infty\). From Section 1.1, it is expected that you know that \(e^{− \infty} = 0\), and therefore, you should be able to conclude that \(y(x)\) decreases from an initial value \(y(0) = a\) to zero. Whether the function will decay to zero slowly or rapidly will depend on the value of \(k\).
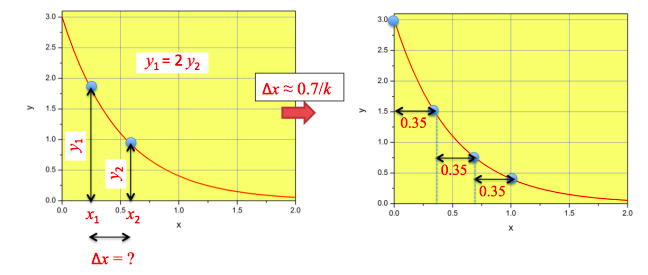
Let’s now consider two points in the curve \(y = ae^{−kx}\)
\[ \begin{array}{c} y_1 = ae^{−kx_1} \\ y_2 = ae^{−kx_2} \end{array} \nonumber\]
and let’s further assume that \(y_1/y_2 = 2\) (see Figure \(\PageIndex{1}\), left). What is the separation between \(x_2\) and \(x_1\) \((\Delta x = x_2 − x_1)\)?
We know that \(y_1/y_2 = 2\), so
\[2 = \frac{e^{-kx_1}}{e^{-kx_2}} \nonumber\]
Using the properties of the exponential function:
\[2 = e^{−k(x_1−x_2)} = e^{−k(− \Delta x)} = e^{k( \Delta x)} \nonumber\]
and solving for \(\Delta x\):
\[ \begin{array}{c} \ln(2) = k( \Delta x) \\ \Delta x = \ln(2)/k \end{array} \nonumber\]
This means that the function decays to 50% of its former value every time we move \(\ln 2/k\) units to the right in the \(x\)−axis.
To sketch the function, we just need to remember that \(\ln(2) \approx 0.7\). Therefore, to sketch \(y = 3e^{−2x}\), we place the first point at \(y = 3\) and \(x = 0\), and the second point at \(y = 3/2\) and \(x \approx 0.7/2 = 0.35\). We can continue adding points following the same logic: every time we drop the value of \(y\) by half, we move \(\ln(2)/k\) units to the right in the \(x\)−axis (see Figure \(\PageIndex{1}\), right).
Sketching an exponential function with negative exponent. http://tinyurl.com/n6pdvyh


