22.3.3: iii. Problems

Q1

Let us investigate the reactions:

\begin{align} i.& &CH_2(^1A_1) &\rightarrow & & H_2 + C\text{, and} \\ ii.& &CH_2(^3B_1) & \rightarrow & & H_2 + C, \end{align}

under an assumed \(C_{2v}\) reaction pathway utilizing the following information:

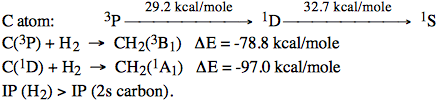
a. Write down (first in terms of \(2p_{1,0,-1}\) orbitals and then in terms of \(2p_{x,y,z}\) orbitals) the:
i. three Slater determinant (SD) wavefunctions belonging to the \(^3P\) state all of which have \(M_S = 1\),
ii. five \(^1\)D SD wavefunctions, and
iii. one \(^1\)S SD wavefunction.

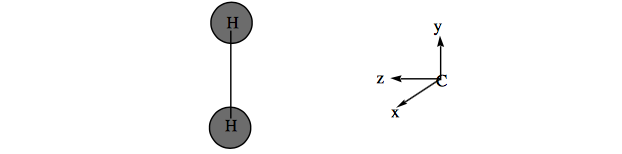
b. Using the coordinate system shown below, label the hydrogen orbitals \(\sigma_g, \sigma_u\) and the carbon 2s, \(2p_x\), \(2p_y\), \(sp_z\), orbitals as \(a_1\text{, }b_1(x)\text{, }b_2(y)\text{, or }a_2\). Do the same for the \(\sigma \text{, } \sigma \text{, } \sigma^{\text{*}}\text{, } \sigma^{\text{*}} \text{, n, and } p_{\pi} \text{ orbitals of } CH_2.\)

c. Draw an orbital correlation diagram for the \(CH_2 \rightarrow H_2 + C\) reactions. Try to represent the relative energy orderings of the orbitals correctly.

d. Draw (on graph paper) a configuration correlation diagram for \(CH_2(^3B_1) \rightarrow H_2 + C\) showing all configurations which arise from the \(C(^3P) + H_2\) products. You can assume the doubly excited configurations like much (~100 kcal / mole) above their parent configurations.

e. Repeat step d. for \(CH_2(^1A_1) \rightarrow H_2 + C\) again showing all configurations which arise from the \(C(^1D) + H_2\) products.

f. Do you expect the reaction \(C(^3P) + H_2 \rightarrow CH_2\) to have a large activation barrier? About how long? What state of \(CH_2\) is produced in this reaction? Would distortions away from \(C_{2v}\) symmetry be expected to raise of lower the activation barrier? Show how one could estimate where along the reaction path the barrier top occurs.

g. Would \(C(^1D) + H_2 \rightarrow CH_2\) be expected to have a larger or smaller barrier than you found for the \(^3P C\) reaction?

Q2

The decomposition of the ground-state single carbene, , to produce acetylene and \(^1\)D carbon is known to occur with an activation energy equal to the reaction endothermicity. However, when triplet carbene decomposes to acetylene and ground-state (triplet) carbon, the activation energy exceeds this reaction's endothermicity. Construct orbital, configuration, and state correlation diagrams which permit you to explain the above observations. Indicate whether single configuration or configuration interaction wavefunctions would be required to describe the above singlet and triplet decomposition processes.

Q3

We want to carry out a configuration interaction calculation on H2 at R=1.40 au. A minimal basis consisting of normalized 1s Slater orbitals with \(\xi\)=1.0 gives rise to the following overlap (S), one-electron (h), and two-electron atomic integrals:

\[ \langle 1S_A | 1S_B \rangle = 0.753 \equiv S, \nonumber \]

\[ \langle 1S_A |h|1s_A \rangle = -1.110, \text{ } \langle 1S_B |h|S_A \rangle = -0.968, \nonumber \]

\[ \langle 1S_A1S_A|h|1S_A1S_A\rangle = 0.625 \equiv \langle AA|AA\rangle \nonumber \]

\[ \langle AA|BB \rangle = 0.323 \text{, } \langle AB|AB \rangle = 0.504 \text{, and} \nonumber \]

\[ \langle AA|AB \rangle = 0.426. \nonumber \]

1. The normalized and orthogonal molecular orbitals we will use for this minimal basis will be determined purely by symmetry: \[ \sigma_g = \dfrac{(1S_A + 1S_B)}{\sqrt{2+2S}} \text{, and } \nonumber \] \[ \sigma_u = \dfrac{(1S_A - 1S_B)}{\sqrt{2+2S}} \nonumber \] Show that these orbitals are indeed orthogonal.
2. Evaluate (using the one- and two- electron atomic integrals given above) the unique one- and two- electron integrals over this molecular orbital basis (this is called a transformation from the ao to the mo basis). For example, evaluate <u|h|u>, <uu|uu>, <gu|gu>, ect.
3. Using the two \(^1\sum\limits_g^+\) configureations \(\sigma_g^2 \text{, and } \sigma_u^2\), show that the elements of the 2x2configuration interaction Hamiltonian matrix are -1.805, 0.140, and -0.568.
4. Using this configureation interaction matrix, find the configuration interaction (CI) approximation to the ground and excited state energies and wavefunctions.
5. Evaluate and make a rough sketch of the polarized orbitals which result from the above ground state \(\sigma_g^2 \text{ and } \sigma_u^2\) CI wavefunction.