7.5: Some Important Applications of Statistical Mechanics
- Page ID
- 17636
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this Section, I introduce several applications of statistical mechanics that are important for students to be aware of because they arise frequently when chemists make use of the tools of statistical mechanics. These examples include
- The basic equations connecting the translational, rotational, vibrational, and electronic properties of isolated (i.e., gas-phase) molecules to their thermodynamics.
- The most basic descriptions of the vibrations of ions, atoms, or molecules within crystals.
- The most elementary models for describing cooperative behavior and phase transitions in gas-surface and liquid-liquid systems.
- The contributions of intermolecular forces to the thermodynamics of gases.
Gas-Molecule Thermodynamics
The equations relating the thermodynamic variables to the molecular partition functions can be employed to obtain the following expressions for the energy \(E\), heat capacity \(C_V\), Helmholz free energy \(A\), entropy \(S\), and chemical potential \(\mu\) in the case of a gas (i.e., in the absence of intermolecular interactions) of polyatomic molecules:
\[\dfrac{E}{NkT} = \dfrac{3}{2} + \dfrac{3}{2} + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \dfrac{h\nu_J/kT} {\exp(h\nu_J/kT)-1} \right] – \dfrac{D_e}{kT},\]
\[\dfrac{C_V}{Nk} = \dfrac{3}{2} + \dfrac{3}{2} + \sum_{J=1}^{3N-6} \left(\dfrac{h\nu_J}{kT}\right)^2 \dfrac{\exp(h\nu_J/kT)}{(\exp(h\nu_J/kT)-1)^2} ,\]
\[-\dfrac{A}{NkT} = \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{V_e}{N}\right) + \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]
\[ - \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] + \dfrac{D_e}{kT} + \ln\omega_e\]
\[\dfrac{S}{Nk} = \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{V_e^{5/2}}{N}\right) + \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]
\[ + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J/kT} {\exp(h\nu_J/kT)-1} – \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] + \ln\omega_e\]
\[\dfrac{\mu}{kT} = - \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{kT}{p}\right) - \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]
\[ + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] - \dfrac{D_e}{kT} - \ln\omega_e.\]
Earlier in this Chapter in Section 7.1.2, we showed how these equations are derived, so I refer the reader back to that treatment for further details.
Notice that, except for the chemical potential \(\mu\), all of these quantities are extensive properties that depend linearly on the number of molecules in the system \(N\). Except for the chemical potential \(\mu\) and the pressure \(p\), all of the variables appearing in these expressions have been defined earlier when we showed the explicit expressions for the translational, vibrational, rotational, and electronic partition functions. These are the working equations that allow one to compute thermodynamic properties of stable molecules, ions, and even reactive species such as radicals in terms of molecular properties such as geometries, vibrational frequencies, electronic state energies and degeneracies, and the temperature, pressure, and volume.
Einstein and Debye Models of Solids
These two models deal with the vibrations of crystals that involve motions among the neighboring atoms, ions, or molecules that comprise the crystal. These inter-fragment vibrations are called phonons. In the Einstein model of a crystal, one assumes that:
- Each atom, ion, or molecule from which the crystal is constituted is trapped in a potential well formed by its interactions with neighboring species. This potential is denoted \(\phi(V/N)\) with the volume-to-number \(\dfrac{V}{N}\) ratio written to keep in mind that it likely depends on the packing density (i.e., the distances among neighbors) within the crystal. Keep in mind that f represents the interaction of any specific atom, ion, or molecule with the \(N-1\) other such species. So, \(\dfrac{N \phi}{2}\), not \(N \phi\) is the total interaction energy among all of the species; the factor of \(\dfrac{1}{2}\) is necessary to avoid double counting.
- Each such species is assumed to undergo local harmonic vibrational motions about its equilibrium position (\(q_J^0\)) within the local well that traps it. If the crystal is isotropic, the force constants \(k_J\) that characterize the harmonic potential \(\dfrac{1}{2} k_J(q_J-q_J^0)^2\) along the \(x\), \(y\), and \(z\) directions are equal; if not, these \(k_J\) parameters may be unequal. It is these force constants, along with the masses \(m\) of the atoms, ions, or molecules, that determine the harmonic frequencies \(\nu_J = \dfrac{1}{2}\pi \sqrt{\dfrac{k_J}{m}}\) of the crystal.
- The inter-species phonon vibrational partition function of the crystal is then assumed to be a product of \(N\) partition functions, one for each atom, ion, or molecule in the crystal, with each partition function taken to be of the harmonic vibrational form:
\[Q = \exp\bigg(-\dfrac{N \phi}{2kT}\bigg) \left\{\prod_{J=1}^3 \dfrac{\exp(-h\nu_J/2kT)}{1-\exp(-h\nu_J/kT)}\right\}^N.\]
There is no factor of \(N!\) in the denominator because, unlike a gas of \(N\) species, each of these \(N\) species (atoms, ions, or molecules) are constrained to stay put (i.e., not free to roam independently) in the trap induced by their neighbors. In this sense, the \(N\) species are distinguishable rather than indistinguishable as they are in the gas case. The \(\dfrac{N\phi}{2kT}\) factor arises when one asks what the total energy of the crystal is, aside from its vibrational energy, relative to \(N\) separated species; in other words, what is the total cohesive energy of the crystal. This energy is \(N\) times the energy of any single species \(\phi\), but, as noted above, divided by 2 to avoid double counting the inter-species interaction energies.
This partition function can be subjected to the thermodynamic equations discussed earlier to compute various thermodynamic properties. One of the most useful to discuss for crystals is the heat capacity \(C_V\), which is given by (see the vibrational contribution to \(C_V\) expressed in Section 7.5.1) :
\[C_V = Nk \sum_{J=1,3} \left(\dfrac{h\nu_J}{kT}\right)^2 \dfrac{\exp(h\nu_J/kT) }{(\exp(h\nu_J/kT) –1)^2}.\]
At very high temperatures, this function can be shown to approach \(3Nk\), which agrees with the experimental observation know as the law of Dulong and Petit. However, at very low temperatures, this expression approaches:
\[C_V \rightarrow \sum_{J=1,3} Nk \left(\dfrac{h\nu_J}{kT}\right)^2 \exp\Big(-\dfrac{h\nu_J}{kT}\Big),\]
which goes to zero as \(T\) approaches zero, but not in a way that is consistent with experimental observation. That is, careful experimental data shows that all crystal heat capacities approach zero proportional to \(T^3\) at low temperature; the Einstein model’s \(C_V\) approaches zero but not in the \(T^3\) form found in experiments.
So, although the Einstein model offers a very useful model of how a crystal’s stability relates to \(N\phi\) and how its \(C_V\) depends on vibrational frequencies of the phonon modes, it does not work well at low temperatures. Nevertheless, it remains a widely used model in which to understand the phonons’ contributions to thermodynamic properties as long as one does not attempt to extrapolate its predictions to low \(T\).
In the Debye model of phonons in crystals, one abandons the view in which each atom, ion, or molecule vibrates independently about it own equilibrium position and replaces this with a view in which the constituent species vibrate collectively in wave-like motions. Each such wave has a wave length \(\lambda\) and a frequency \(\nu\) that are related to the speed \(c\) of propagation of such waves in the crystal by
\[c = \lambda \nu.\]
The speed \(c\) is a characteristic of the crystal’s inter-species forces; it is large for stiff crystals and small for soft crystals.
In a manner much like we used to determine the density of quantum states \(\Omega(E)\) within a three-dimensional box, one can determine how many waves can fit within a cubic crystalline box having frequencies between \(\nu\) and \(\nu + d\nu\). The approach to this problem is to express the allowed wave lengths and frequencies as:
\[\lambda_n = \dfrac{2L}{n},\]
\[\nu_n = \dfrac{n c}{2L},\]
where \(L\) is the length of the box on each of its sides and \(\nu\) is an integer \(1, 2, 3, \cdots\). This prescription forces all wave lengths to match the boundary condition for vanishing at the box boundaries.
Then carrying out a count of how many (\(\Omega(\nu)\)) waves have frequencies between \(\nu\) and \(\nu + d\nu\) for a box whose sides are all equal gives the following expression:
\[\Omega(\nu) = \dfrac{12\pi V \nu^2}{c^3}.\]
The primary observation to be made is that the density of waves is proportional to \(\nu^2\):
\[\Omega(\nu) = a \nu^2.\]
It is conventional to define the parameter a in terms of the maximum frequency \(\nu_m\) that one obtains by requiring that the integral of \(\Omega(\nu)\) over all allowed \(\nu\) add up to \(3N\), the total number of inter-species vibrations that can occur:
\[3N = \int \Omega(\nu) d\nu = \dfrac{a \nu_m^3}{3}.\]
This then gives the constant a in terms of \(\nu_m\) and \(N\) and allows \(\Omega(\nu)\) to be written as
\[\Omega(\nu) = \dfrac{9N}{\nu_m^3}.\]
The Debye model uses this wave picture and computes the total energy \(E\) of the crystal much as done in the Einstein model, but with the sum over \(3N\) vibrational modes replaced by a continuous integral over the frequencies \(\nu\) weighted by the density of such states \(\Omega(\nu)\) ((see the vibrational contribution to \(E\) expressed in Section 7.5.1):
\[E = \dfrac{N\phi}{2} + \dfrac{9NkT}{\nu_m^3} \int \left[\dfrac{h\nu}{2kT} + \dfrac{h\nu /kT}{\exp(h\nu /kT) –1} \right]\nu^2 d\nu,\]
where the integral over \(\nu\) ranges from 0 to nm. It turns out that the \(C_V\) heat capacity obtained by taking the temperature derivative of this expression for \(E\) can be written as follows:
\[C_V = 3Nk \left[ 4 D\dfrac{h\nu_m}{kT} – \dfrac{3(h\nu_m/kT)}{\exp(h\nu_m/kT) –1} \right]\]
where the so-called Debye function \(D(u)\) is defined by
\[D(u) = 3 u^{-3} \int \dfrac{x^3}{\exp(x) – 1} dx,\]
and the integral is taken from \(x = 0\) to \(x = u\).
The important thing to be noted about the Debye model is that the heat capacity, as defined above, extrapolates to \(3Nk\) at high temperatures, thus agreeing with the law of Dulong and Petit, and varies at low temperature as
\[C_V \rightarrow \dfrac{12}{5} Nk\pi^4 \left(\dfrac{kT}{h\nu_m}\right)^3.\]
So, the Debye heat capacity does indeed vary as \(T^3\) at low \(T\) as careful experiments indicate. For this reason, it is appropriate to use the Debye model whenever one is interested in properly treating the energy, heat capacity, and other thermodynamic properties of crystals at temperatures for which \(\dfrac{kT}{h\nu_m}\) is small. At higher temperatures, it is appropriate to use either the Debye or Einstein models. The major difference between the two lies in how they treat the spectrum of vibrational frequencies that occur in a crystal. The Einstein model says that only one (or at most three, if three different \(k_J\) values are used) frequency occurs \(\nu_J = \dfrac{1}{2}\pi \sqrt{\dfrac{k_J}{m}}\); each species in the crystal is assumed to vibrate at this frequency. In contrast, the Debye model says that the species vibrate collectively and with frequencies ranging from \(n = 0\) up to \(\nu = \nu_m\), the so-called Debye frequency, which is proportional to the speed \(c\) at which phonons propagate in the crystal. In turn, this speed depends on the stiffness (i.e., the inter-species potentials) within the crystal.
Lattice Theories of Surfaces and Liquids
This kind of theory can be applied to a wide variety of chemical and physical problems, so it is a very useful model to be aware of. The starting point of the model is to consider a lattice containing \(M\) sites, each of which has \(c\) nearest neighbor sites (n.b., clearly, \(c\) will depend on the structure of the lattice) and to imagine that each of these sites can exist in either of two states that we label A and B. Before deriving the basic equations of this model, let me explain how the concepts of sites and A and B states are used to apply the model to various problems.
- The sites can represent binding sites on the surface of a solid and the two states A and B can represent situations in which the site is either occupied (A) or unoccupied (B) by a molecule that is chemisorbed or physisorbed to the site. This point of view is taken when one applies lattice models to adsorption of gases or liquids to solid surfaces.
- The sites can represent individual spin = 1/2 molecules or ions within a lattice, and the states A and B can denote the a and b spin states of these species. This point of view allows the lattice models to be applied to magnetic materials.
- The sites can represent positions that either of two kinds of molecules A and B might occupy in a liquid or solid in which case A and B are used to label whether each site contains an A or a B molecule. This is how we apply the lattice theories to liquid mixtures.
- The sites can represent cis- and trans- conformations in linkages within a polymer, and A and B can be used to label each such linkage as being either cis- or trans-. This is how we use these models to study polymer conformations.
In Figure 7.4, I show a two-dimensional lattice having 25 sites of which 16 are occupied by dark (A) species and 9 are occupied by lighter (B) species.

The partition function for such a lattice is written in terms of a degeneracy \(\Omega\) and an energy \(E\), as usual. The degeneracy is computed by considering the number of ways a total of \(N_A + N_B\) species can be arranged on the lattice:
\[\Omega = \dfrac{(N_A+N_B)!}{N_A! N_B!}.\]
The interaction energy among the A and B species for any arrangement of the A and B on the lattice is assumed to be expressed in terms of pair wise interaction energies. In particular, if only nearest neighbor interaction energies are considered, one can write the total interaction energy \(E_{\rm int}\) of any arrangement as
\[E_{\rm int} = N_{AA} E_{AA} + N_{BB} E_{BB} + N_{AB} E_{AB}\]
where \(N_{IJ}\) is the number of nearest neighbor pairs of type I-J and \(E_{IJ}\) is the interaction energy of an I-J pair. The example shown in Figure 7.4 has \(N_{AA} = 16\), \(N_{BB} = 4\) and \(N_{AB} = 19\).
The three parameters \(N_{IJ}\) that characterize any such arrangement can be re-expressed in terms of the numbers \(N_A\) and \(N_B\) of A and B species and the number of nearest neighbors per site \(c\) as follows:
\[2N_{AA} + N_{AB} = cN_A\]
\[2N_{BB} + N_{AB} = cN_B.\]
Note that the sum of these two equations states the obvious fact that twice the sum of AA, BB, and AB pairs must equal the number of A and B species multiplied by the number of neighbors per species, \(c\).
Using the above relationships among \(N_{AA}\), \(N_{BB}\), and \(N_{AB}\), we can rewrite the interaction energy as
\[E_{\rm int} = E_{AA} \dfrac{c N_A – N_{AB}}{2} + E_{BB} \dfrac{c N_B – N_{AB}}{2} + E_{AB} N_{AB}\]
\[=\dfrac{(N_A E_{AA} + N_B E_{BB}) c}{2} + \dfrac{(2 E_{AB} – E_{AA} – E_{BB} ) N_{AB}}{2}\]
The reason it is helpful to write \(E_{\rm int}\) in this manner is that it allows us to express things in terms of two variables over which one has direct experimental control, \(N_A\) and \(N_B\), and one variable \(N_{AB}\) that characterizes the degree of disorder among the A and B species. That is, if \(N_{AB}\) is small, the A and B species are arranged on the lattice in a phase-separated manner; whereas, if \(N_{AB}\) is large, the A and B are well mixed.
The total partition function of the A and B species arranged on the lattice is written as follows:
\[Q = q_A^{N_A} q_B^{N_B} \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}) \exp(-E_{\rm int}/kT).\]
Here, \(q_A\) and \(q_B\) are the partition functions (electronic, vibrational, etc.) of the A and B species as they sit bound to a lattice site and \(\Omega(N_A, N_B, N_{AB})\) is the number of ways that \(N_A\) species of type A and \(N_B\) of type B can be arranged on the lattice such that there are \(N_{AB}\) A-B type nearest neighbors. Of course, \(E_{\rm int}\) is the interaction energy discussed earlier. The sum occurs because a partition function is a sum over all possible states of the system. There are no (\(1/N_J!\)) factors because, as in the Einstein and Debye crystal models, the A and B species are not free to roam but are tied to lattice sites and thus are distinguishable.
This expression for \(Q\) can be rewritten in a manner that is more useful by employing the earlier relationships for \(N_{AA}\) and \(N_{BB}\):
\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}) \exp\Bigl(\dfrac{N_{AB}X}{2kT}\Bigr),\]
where
\[X = (-2 E_{AB} + E_{AA} + E_{BB} ).\]
The quantity \(X\) plays a central role in all lattice theories because it provides a measure of how different the A-B interaction energy is from the average of the A-A and B-B interaction energies. As we will soon see, if \(X\) is large and negative (i.e., if the A-A and B-B interactions are highly attractive), phase separation can occur; if \(X\) is positive, phase separation will not occur.
The problem with the above expression for the partition function is that no one has yet determined an analytical expression for the degeneracy \(\Omega(N_A, N_B, N_{AB})\) factor. Therefore, in the most elementary lattice theory, known as the Bragg-Williams approximation, one approximates the sum over \(N_{AB}\) by taking the following average value of \({AB}\):
\[N_{AB}^* = \dfrac{N_A(cN_B)}{N_A+N_B}\]
in the expression for \(\Omega\). This average is formed by taking the number of A sites and multiplying by the number of neighbor sites (c) and by the fraction of these neighbor sites that would be occupied by a B species if mixing were random. This approximation produces
\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \exp\Bigl(\dfrac{N_{AB}^*X}{2kT}\Bigr) \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}).\]
Finally, we realize that the sum \(\sum_{N_{AB}} \Omega(N_A, N_B, N_{AB})\) is equal to the number of ways of arranging \(N_A\) A species and \(N_B\) B species on the lattice regardless of how many A-B neighbor pairs there are. This number is, of course, \(\dfrac{(N_A+N_B)!}{N_A!N_B!}\).
So, the Bragg-Williams lattice model partition function reduces to:
\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \dfrac{(N_A+N_B)!}{N_A!N_B!} \exp\Bigl(\dfrac{N_{AB}^*X}{2kT}\Bigr).\]
The most common connection one makes to experimental measurements using this partition function arises by computing the chemical potentials of the A and B species on the lattice and equating these to the chemical potentials of the A and B as they exist in the gas phase. In this way, one uses the equilibrium conditions (equal chemical potentials in two phases) to relate the vapor pressures of A and B, which arise through the gas-phase chemical potentials, to the interaction energy \(X\).
Let me now show you how this is done. First, we use
\[\mu_J = -kT \left(\dfrac{∂\ln Q}{∂N_J}\right)_{T,V}\]
to compute the A and B chemical potentials on the lattice. This gives
\[\mu_A = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln\Bigl(\dfrac{N_A}{N_A+N_B}\Bigr) + \Bigl(1-\dfrac{N_A}{N_A+N_B}\Bigr)^2 \dfrac{cX}{2kT} \right\}\]
and an analogous expression for \(\mu_B\) with \(N_B\) replacing \(N_A\). The expression for the gas-phase chemical potentials \(\mu_A^g\) and \(\mu_B^g\) given earlier in this Chapter has the form:
\[\mu = - kT \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{kT}{p}\right) – kT \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]
\[+kT \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] - D_e – kT \ln\omega_e,\]
within which the vapor pressure appears. The pressure dependence of this gas-phase expression can be factored out to write each \(\mu\) as:
\[\mu_A^g = \mu_A^0 + kT \ln(p_A),\]
where \(p_A\) is the vapor pressure of A (in atmosphere units) and \(\mu_A^0\) denotes all of the other factors in \(\mu_A^g\). Likewise, the lattice-phase chemical potentials can be written as a term that contains the \(N_A\) and \(N_B\) dependence and a term that does not:
\[\mu_A = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln X_A + (1-X_A)^2 \dfrac{cX}{2kT} \right\},\]
where \(X_A\) is the mole fraction of A (\(\dfrac{N_A}{N_A+N_B}\)). Of course, an analogous expression holds for \(\mu_B\).
We now perform two steps:
- We equate the gas-phase and lattice-phase chemical potentials of species A in a case where the mole fraction of A is unity. This gives \[\mu_A^0 + kT \ln(p_A^0) = -kT{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)}\] where \(p_A^0\) is the vapor pressure of A that exists over the lattice in which only A species are present.
- We equate the gas- and lattice-phase chemical potentials of A for an arbitrary chemical potential \(X_A\) and obtain: \[\mu_A^0 + kT \ln(p_A) = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln X_A + (1-X_A)^2 \dfrac{cX}{2kT} \right\},\] which contains the vapor pressure \(p_A\) of A over the lattice covered by A and B with \(X_A\) being the mole fraction of A.
Subtracting these two equations and rearranging, we obtain an expression for how the vapor pressure of A depends on \(X_A\):
\[p_A = p_A^0 X_A \exp\Bigl(-\dfrac{cX(1-X_A)^2}{2kT}\Bigr).\]
Recall that the quantity \(X\) is related to the interaction energies among various species as
\[X = (-2 E_{AB} + E_{AA} + E_{BB} ).\]
Let us examine that physical meaning of the above result for the vapor pressure. First, if one were to totally ignore the interaction energies (i.e., by taking \(X = 0\)), one would obtain the well known Raoult’s Law expression for the vapor pressure of a mixture:
\[p_A = p_A^0 X_A\]
\[p_B = p_B^0 X_B.\]
In Figure 7.5, I plot the A and B vapor pressures vs. \(X_A\). The two straight lines are, of course, just the Raoult’s Law findings. I also plot the \(p_A\) vapor pressure for three values of the \(X\) interaction energy parameter. When \(X\) is positive, meaning that the A-B interactions are more energetically favorable than the average of the A-A and B-B interactions, the vapor pressure of A is found to deviate negatively from the Raoult’s Law prediction. This means that the observed vapor pressure is lower than is that expected based solely on Raoult’s Law. On the other hand, when \(X\) is negative, the vapor pressure deviates positively from Raoult’s Law.
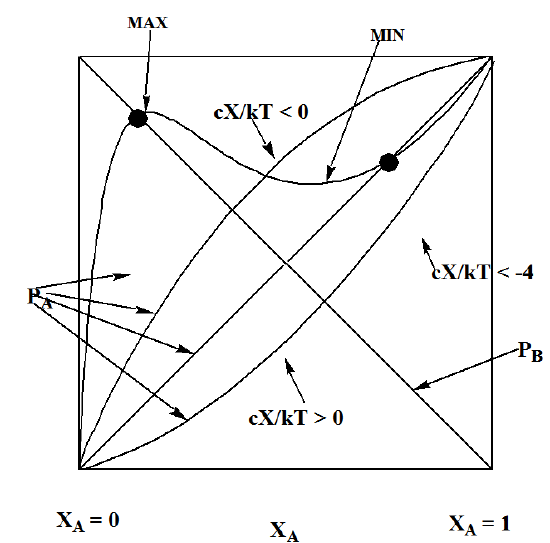
An especially important and interesting case arises when the \(X\) parameter is negative and has a value that makes \(\dfrac{cX}{2kT}\) be more negative than –4. It turns out that in such cases, the function \(p_A\) suggested in this Bragg-Williams model displays a behavior that suggests a phase transition may occur. Hints of this behavior are clear in Figure 7.5 where one of the plots displays both a maximum and a minimum, but the plots for \(X > 0\) and for \(\dfrac{cX}{2kT} > -4\) do not. Let me now explain this further by examining the derivative of \(p_A\) with respect to \(X_A\):
\[\dfrac{dp_A}{dX_A} = p_A^0 \left\{1 + X_A(1-X_A) \dfrac{2cX}{2kT}\right\} \exp\Bigl(-\dfrac{cX(1-X_A)^2}{2kT}\Bigr).\]
Setting this derivative to zero (in search of a maximum or minimum), and solving for the values of \(X_A\) that make this possible, one obtains:
\[X_A= \dfrac{1 ± \sqrt{1+4kT/cX} }{2}.\]
Because \(X_A\) is a mole fraction, it must be less than unity and greater than zero. The above result giving the mole fraction at which \(\dfrac{dp_A}{dX_A} = 0\) will not produce a realistic value of \(X_A\) unless
\[\dfrac{cX}{kT} < - 4.\]
If \(\dfrac{cX}{kT} = -4\), there is only one value of \(X_A\) (i.e., \(X_A\) = 1/2) that produces a zero slope; for \(\dfrac{cX}{kT} < -4\), there will be two such values given by \(X_A = \dfrac{1 ± \sqrt{1+4kT/cX} }{2}\), which is what we see in Figure 7.5 where the plot displays both a maximum and a minimum.
What does it mean for \(\dfrac{cX}{kT}\) to be less than \(-4\) and why is this important? For \(X\) to be negative, it means that the average of the A-A and B-B interactions are more energetically favorable than is the A-B interactions. It is for this reason that a phase separation is may be favored in such cases (i.e., the A species prefer to be near other A species more than to be near B species, and similarly for the B species). However, thermal motion can overcome a slight preference for such separation. That is, if \(X\) is not large enough, \(kT\) can overcome this slight preference. This is why \(cX\) must be less than \(-4kT\), not just less than zero.
So, the bottom line is that if the A-A and B-B interactions are more attractive, on average, than are the A-B interactions, one can experience a phase separation in which the A and B species do not remain mixed on the lattice but instead gather into two distinct kinds of domains. One domain will be rich in the A species, having an \(X_A\) value equal to that shown in the right dot in Figure 7.5. The other domains will be rich in B and have an \(X_A\) value of that shown by the left dot.
As I noted in the introduction to this Section, lattice models can be applied to a variety of problems. We just analyzed how it is applied, within the Bragg-Williams approximation, to mixtures of two species. In this way, we obtain expressions for how the vapor pressures of the two species in the liquid or solid mixture display behavior that reflects their interaction energies. Let me now briefly show you how the lattice model is applied in some other areas.
In studying adsorption of gases to sites on a solid surface, one imagines a surface containing M sites per unit area A with \(N_{ad}\) molecules (that have been adsorbed from the gas phase) bound to these sites. In this case, the interaction energy \(E_{\rm int}\) introduced earlier involves only interactions among neighboring adsorbed molecules; there are no lateral interactions among empty surface sites or between empty surface sites and adsorbed molecules. So, we can make the following replacements in our earlier equations:
\[N_A \rightarrow N_{ad}\]
\[N_B \rightarrow M – N_{ad}\]
\[E_{\rm int} = E_{ad,ad} N_{ad,ad},\]
where \(N_{ad,ad}\) is the number of nearest neighbor pairs of adsorbed species and \(E_{ad,ad}\) is the pairwise interaction energy between such a pair. The primary result obtained by equating the chemical potentials of the gas-phase and adsorbed molecules is:
\[p = kT \dfrac{q_{gas}}{V} \dfrac{1}{q_{ad}} \dfrac{\theta}{1-\theta} \exp\Big(\dfrac{E_{ad}c\theta}{kT}\Big).\]
Here \(q_{gas}/V\) is the partition function of the gas-phase molecules per unit volume, \(q_{ad}\) is the partition function of the adsorbed molecules (which contains the adsorption energy as \(\exp(-\phi /kT))\) and \(\theta\) is called the coverage (i.e., the fraction of surface sites to which molecules have adsorbed). Clearly, \(\theta\) plays the role that the mole fraction \(X_A\) played earlier. This so-called adsorption isotherm equation allows one to connect the pressure of the gas above the solid surface to the coverage.
As in our earlier example, something unusual occurs when the quantity \(E_{ad}c\theta/kT\) is negative and beyond a critical value. In particular, differentiating the expression for \(p\) with respect to \(\theta\) and finding for what \(\theta\) value(s) \(dp/d\theta\) vanishes, one finds:
\[q = \dfrac{ 1 ± \sqrt{1 +4kT/cE_{ad}} }{2}.\]
Since \(\theta\) is a positive fraction, this equation can only produce useful values if
\[\dfrac{cE_{ad}}{kT} < -4.\]
In this case, this means that if the attractions between neighboring adsorbed molecules is strong enough, it can overcome thermal factors to cause phase-separation to occur. The kind of phase separation on observes is the formation of islands of adsorbed molecules separated by regions where the surface has little or no adsorbed molecules.
There is another area where this kind of lattice model is widely used. When studying magnetic materials one often uses the lattice model to describe the interactions among pairs of neighboring spins (e.g., unpaired electrons on neighboring molecules or nuclear spins on neighboring molecules). In this application, one assumes that up or down spin states are distributed among the lattice sites, which represent where the molecules are located. \(N_\alpha\) and \(N_\beta\) are the total number such spins, so (\(N_\alpha - N_\beta\)) is a measure of what is called the net magnetization of the sample. The result of applying the Bragg-Williams approximation in this case is that one again observes a critical condition under which strong spin pairings occur. In particular, because the interactions between a and a spins, denoted \(–J\), and between \(\alpha\) and \(\beta\) spins, denoted \(+ J\), are equal and opposite, the \(X\) variable characteristic of all lattice models reduces to:
\[X = -2E_{\alpha,\beta} + E_{\alpha,\alpha} + E_{\beta,\beta} = -4 J.\]
The critical condition under which one expects like spins to pair up and thus to form islands of a-rich centers and other islands of b-rich centers is
\[-\dfrac{4 cJ}{kT} < - 4\]
or
\[\dfrac{cJ}{kT} > 1.\]
Virial Corrections to Ideal-Gas Behavior
Recall from our earlier treatment of classical partition function that one can decompose the total partition function into a product of two factors:
\[Q = \dfrac{h^{-NM}}{N!}\int \exp \Big(- \dfrac{H^0(y, p)}{kT}\Big) dy dp \int \exp \Big(-\dfrac{U(r)}{kT}\Big) dr\]
one of which
\[Q_{\rm ideal} = \dfrac{h^{-NM}}{N!} \int \exp \Big(- \dfrac{H^0(y, p)}{kT}\Big) dy dp V^N\]
is the result if no intermolecular potentials are operative. The second factor
\[Q_{\rm inter} = \dfrac{1}{V^N} {\int \exp \Big(-\dfrac{U(r)}{kT}\Big) dr}\]
thus contains all of the effects of intermolecular interactions. Recall also that all of the equations relating partition functions to thermodynamic properties involve taking \(\ln Q\) and derivatives of \(\ln Q\). So, all such equations can be cast into sums of two parts; that arising from \(\ln Q_{\rm ideal}\) and that arising from \( \ln Q_{\rm inter}\). In this Section, we will be discussing the contributions of \(Q_{\rm inter}\) to such equations.
The first thing that is done to develop the so-called cluster expansion of \(Q_{\rm inter}\) is to assume that the total intermolecular potential energy can be expressed as a sum of pair wise additive terms:
\[U = \sum_{I<J} U(r_{IJ})\]
where \(r_{IJ}\) labels the distance between molecule \(I\) and molecule \(J\). This allows the exponential appearing in \(Q_{\rm inter}\) to be written as a product of terms, one for each pair of molecules:
\[\exp\Big(-\dfrac{U}{kT}\Big) = \exp\Big(- \sum_{I<J} \dfrac{U(r_{IJ})}{kT}\Big) = \prod_{I<J} \exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big).\]
Each of the exponentials \(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big)\) is then expressed as follows:
\[\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big) = 1 + \Big(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big) –1\Big) = 1 + f_{IJ},\]
the last equality being what defines \(f_{IJ}\). These \(f_{IJ}\) functions are introduced because, whenever the molecules \(I\) and \(J\) are distant from one another and thus not interacting, \(U(r_{IJ})\) vanishes, so \(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big)\) approaches unity, and thus \(f_{IJ}\) vanishes. In contrast, whenever molecules \(I\) and \(J\) are close enough to experience strong repulsive interactions, \(U(r_{IJ})\) is large and positive, so \(f_{IJ}\) approaches \(-1\). These properties make \(f_{IJ}\) a useful measure of how molecules are interacting; if they are not, \(f = 0\), if they are repelling strongly, \(f = -1\), and if they are strongly attracting, \(f\) is large and positive.
Inserting the \(f_{IJ}\) functions into the product expansion of the exponential, one obtains:
\[\exp\Big(-\dfrac{U}{kT}\Big) = \prod_{I<J} (1 + f_{IJ}) = 1 + \sum_{I<J} f_{IJ} + \sum_{I<J} \sum_{K<L} f_{IJ} f_{KL} + \cdots\]
which is called the cluster expansion in terms of the \(f_{IJ}\) pair functions. When this expansion is substituted into the expression for \(Q_{\rm inter}\), we find:
\[Q_{\rm inter} = \dfrac{1}{V^N} \int (1 + \sum_{I<J} f_{IJ} + \sum_{I<J} \sum_{K<L} f_{IJ} f_{KL} + \cdots) dr\]
where the integral is over all \(3N\) of the \(N\) molecule’s center of mass coordinates.
The integrals involving only one \(f_{IJ}\) function are all equal (i.e., for any pair \(I\), \(J\), the molecules are identical in their interaction potentials) and reduce to:
\[\dfrac{N(N-1)}{2V^2} \int f(r_1,2) dr_1 dr_2.\]
The integrals over \(dr_3 \cdots dr_N\) produce \(V^{N-2}\), which combines with \(\dfrac{1}{V^N}\) to produce the \(V^{-2}\) seen. Finally, because \(f(r_{1,2})\) depends only on the relative positions of molecules 1 and 2, the six dimensional integral over \(dr_1 dr_2\) can be replaced by integrals over the relative location of the two molecules r, and the position of their center of mass \(R\). The integral over \(R\) gives one more factor of \(V\), and the above cluster integral reduces to
\[4\pi \dfrac{N(N-1)}{2V} \int f(r) r^2 dr.\]
with the \(4\pi\) coming from the angular integral over the relative coordinate \(r\). Because the total number of molecules \(N\) is very large, it is common to write the \(\dfrac{N(N-1)}{2}\) factor as \(\dfrac{N^2}{2}\).
The cluster integrals containing two \(f_{IJ} f_{KL}\) factors can also be reduced. However, it is important to keep track of different kinds of such factors (depending on whether the indices \(I\), \(J\), \(K\), \(L\) are all different or not). For example, terms of the form
\[\dfrac{1}{V^N} \int f_{IJ} f_{KL} dr_1 dr_2 \cdots dr_N\]
with \(I\), \(J\), \(K\), and \(L\) all unique.
reduce (again using the equivalence of the molecules and the fact that \(f_{IJ}\) depends only on the relative positions of \(I\) and J) to:
\[\dfrac{N^4}{4} (4\pi)^2 V^{-2} \int f_{12} r_{12}^2 dr_{12} \int f_{34} r_{34}^2 dr_{34},\]
where, again I used the fact that \(N\) is very large to replace \(\dfrac{N(N-1)}{2} \dfrac{(N-2)(N-3)}{2}\) by \(\dfrac{N^4}{4}\).
On the other hand, cluster integrals with, for example,\( I=K\) but \(J\) and \(L\) different reduce as follows:
\[\dfrac{1}{V^N} \int f_{12} f_{13} dr_1 dr_2 \cdots dr_N = \dfrac{1}{2} V^{-3} N^3 \int f_{12} f_{13} dr_1 dr_2 dr_3.\]
Because \(f_{12}\) depends only on the relative positions of molecules 1 and 2 and \(f_{13}\) depends on the relative positions of 1 and 3, the nine-dimensional integral over \(dr_1 dr_2 dr_3\) can be changed to a six-dimensional integral over \(dr_{12} dr_{13}\) and an integral over the location of molecule 1; the latter integral produces a factor of \(V\) when carried out. Thus, the above cluster integral reduces to:
\[(4\pi)^2 \dfrac{1}{2} V^{-2} N^3 \int f_{12} f_{13} r_{12}^2 r_{13}^2 dr_{12} dr_{13} .\]
There is a fundamental difference between cluster integrals of the type \(f_{12} f_{34}\) and those involving \(f_{12} f_{13}\). The former are called unlinked clusters because they involve the interaction of molecules 1 and 2 and a separate interaction of molecules 3 and 4. The latter are called linked because they involve molecule 1 interacting simultaneously with molecules 2 and 3 (although 2 and 3 need not be close enough to cause \(f_{23}\) to be non-zero). The primary differences between unlinked and linked cluster contributions are:
- The total number of unlinked terms is proportional to \(N^4\), while the number of linked terms is proportional to \(N^3\). This causes the former to be more important than the latter because they are more numerous.
- The linked terms only become important at densities where there is a significant probability that three molecules occupy nearby regions of space. The unlinked terms, on the other hand, do not require that molecules 1 and 2 be anywhere near molecules 3 and 4. This also causes the unlinked terms to dominate especially at low and moderate densities.
I should note that a similar observation was made in Chapter 6 when we discussed the configuration interaction and coupled-cluster expansion of electronic wave functions. That is, we noted that doubly excited configurations (analogous to \(f_{IJ}\)) are the most important contributions beyond the single determinant, and that quadruple excitations in the form of unlinked products of double excitations were next most important, not triple excitations. The unlinked nature in this case was related to the amplitudes of the quadruple excitations being products of the amplitudes of two double excitations. So, both in electronic structures and in liquid structure, one finds that pair correlations followed by unlinked pair correlations are the most important to consider.
Clearly, the cluster expansion approach to \(Q_{\rm inter}\) can be carried to higher and higher-level clusters (e.g., involving \(f_{12} f_{34} f_{56}\) or \(f_{12} f_{13} f_{34}\), etc.). Generally, one finds that the unlinked terms (e.g., \(f_{12} f_{34} f_{56}\) in this example) are most important (because they are proportional to higher powers of \(N\) and because they do not require more than binary collisions). It is most common, however, to employ a severely truncated expansion and to retain only the linked terms. Doing so for \(Q_{\rm inter}\) produces at the lower levels:
\[Q_{\rm inter} = 1 + \dfrac{1}{2} \Big(\dfrac{N}{V}\Big)^2 4\pi V \int f r^2 dr + \dfrac{1}{4} \Big(\dfrac{N}{V}\Big)^4 [4\pi V \int f r^2 dr ]^2\]
\[+ \dfrac{1}{2} \Big(\dfrac{N}{V}\Big)^3 V (4\pi)^2 \int f_{12} f_{13} r_{12}^2 r_{13}^2 dr_{12} dr_{13}.\]
One of the most common properties to compute using a partition function that includes molecular interactions in the cluster manner is the pressure, which is calculated as:
\[p = kT \left(\dfrac{∂\ln Q}{∂V}\right)_{N,T}.\]
Using \(Q = Q_{\rm ideal} Q_{\rm inter}\) and inserting the above expression for \(Q_{\rm inter}\) produces the following result for the pressure:
\[\dfrac{pV}{NkT} = 1 + B_2 \Big(\dfrac{N}{V}\Big) + B_3 \Big(\dfrac{N}{V}\Big)^2 + \cdots\]
where the so-called virial coefficients \(B_2\) and \(B_3\) are defined as the factors proportional to \(\Big(\dfrac{N}{V}\Big)\) and \(\Big(\dfrac{N}{V}\Big)^2\), respectively. The second virial coefficient’s expression in terms of the cluster integrals is:
\[B_2 = - 2\pi \int f r^2 dr = - 2\pi \int \Big[\exp\Big(-\dfrac{U(r)}{kT}\Big) –1\Big] r^2 dr.\]
The third virial coefficient involves higher order cluster integrals.
The importance of such cluster analysis is that they allow various thermodynamic properties (e.g., the pressure above) to be expressed as one contribution that would occur if the system consisted of non-interacting molecules and a second contribution that arises from the intermolecular forces. It thus allows experimental measurements of the deviation from ideal (i.e., non-interacting) behavior to provide a direct way to determine intermolecular potentials. For example, by measuring pressures at various \(N/V\) values and various temperatures, one can determine \(B_2\) and thus gain valuable information about the intermolecular potential \(U\).
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


