6.9: Experimental Probes of Electronic Structure
- Page ID
- 11590
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Visible and Ultraviolet Spectroscopy
Visible and ultraviolet spectroscopies are used to study transitions between states of a molecule or ion in which the electrons’ orbital occupancy changes. We call these electronic transitions, and they usually require light in the 5000 cm\(^{-1}\) to 100,000 cm\(^{-1}\) regime. When such transitions occur, the initial and final states generally differ in their electronic, vibrational, and rotational energies because any change to the electrons' orbital occupancy will induce changes in the Born-Oppenheimer energy surface which, in turn, governs the vibrational and rotational character. Excitations of inner-shell and core orbital electrons may require even higher energy photons as would excitations that eject an electron. The interpretation of all such spectroscopic data relies heavily on theory as this Section is designed to illustrate.
The Electronic Transition Dipole and Use of Point Group Symmetry
The interaction of electromagnetic radiation with a molecule's electrons and nuclei can be treated using perturbation theory as we discussed in Chapter 4. The result is a standard expression that we derived in Chapter 4
\[R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2\]
for the rate of photon absorption between initial \(\Phi_i\) and final \(\Phi_f\) states. In this equation, \(f(\omega)\) is the intensity of the photon source at the frequency \(\omega\), \(\omega_{f,i}\) is the frequency corresponding to the transition under study, and \(\textbf{E}_0\) is the electric field vector of the photon field. The vector \(\boldsymbol{\mu}\) is the electric dipole moment of the electrons and nuclei in the molecule.
Because each of these wave functions is a product of an electronic ye, a vibrational, and a rotational function, we realize that the electronic integral appearing in this rate expression involves
\[\langle \psi_{ef} | \boldsymbol{\mu} | \psi_{ei}\rangle = \boldsymbol{\mu}_{f,i} (R),\]
a transition dipole matrix element between the initial \(\psi_{ei}\) and final \(\psi_{ef}\) electronic wave functions. This element is a function of the internal vibrational coordinates of the molecule, and is a vector locked to the molecule's internal axis frame.
Molecular point-group symmetry can often be used to determine whether a particular transition's dipole matrix element will vanish and, as a result, the electronic transition will be forbidden and thus predicted to have zero intensity. If the direct product of the symmetries of the initial and final electronic states \(\psi_{ei}\) and \(\psi_{ef}\) do not match the symmetry of the electric dipole operator (which has the symmetry of its \(x\), \(y\), and \(z\) components; these symmetries can be read off the right most column of the character tables), the matrix element will vanish.
For example, the formaldehyde molecule \(H_2CO\) has a ground electronic state that has \(^1A_1\) symmetry in the \(C_{2v}\) point group. Its \(\pi \Rightarrow \pi^*\) singlet excited state also has \(^1A_1\) symmetry because both the \(\pi\) and \(\pi^*\) orbitals are of \(b_1\) symmetry. In contrast, the lowest \(n \Rightarrow \pi^*\) (these orbitals are shown in Figure 6.15) singlet excited state is of \(^1A_2\) symmetry because the highest energy oxygen centered non-bonding orbital is of \(b_2\) symmetry and the \(\pi^*\) orbital is of \(b_1\) symmetry, so the Slater determinant in which both the \(n\) and \(\pi^*\) orbitals are singly occupied has its symmetry dictated by the \(b_2 \times b_1\) direct product, which is \(A_2\).
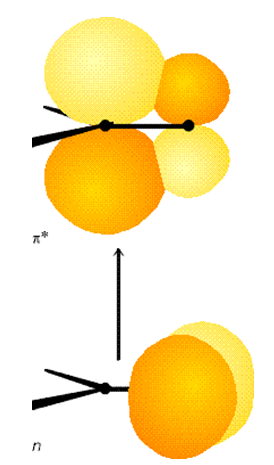
The \(\pi \Rightarrow \pi^*\) transition thus involves ground (\(^1A_1\)) and excited (\(^1A_1\)) states whose direct product (\(A_1 \times A_1\)) is of \(A_1\) symmetry. This transition thus requires that the electric dipole operator possess a component of \(A_1\) symmetry. A glance at the \(C_{2v}\) point group's character table shows that the molecular \(z\)-axis is of \(A_1\) symmetry. Thus, if the light's electric field has a non-zero component along the \(C_2\) symmetry axis (the molecule's \(z\)-axis), the \(\pi \Rightarrow \pi^*\) transition is predicted to be allowed. Light polarized along either of the molecule's other two axes cannot induce this transition.
In contrast, the \(n \Rightarrow \pi^*\) transition has a ground-excited state direct product of \(B_2\times B_1=A_2\) symmetry. The \(C_{2v}\)'s point group character table shows that the electric dipole operator (i.e., its \(x\), \(y\), and \(z\) components in the molecule-fixed frame) has no component of \(A_2\) symmetry; thus, light of no electric field orientation can induce this \(n \Rightarrow \pi^*\) transition. We thus say that the \(n \Rightarrow \pi^*\) transition is forbidden.
The above examples illustrate one of the most important applications of visible-UV spectroscopy. The information gained in such experiments can be used to infer the symmetries of the electronic states and hence of the orbitals occupied in these states. It is in this manner that this kind of experiment probes electronic structures.
The Franck-Condon Factors
Beyond such electronic symmetry analysis, it is also possible to derive vibrational selection rules for electronic transitions that are allowed. It is conventional to expand the transition dipole matrix element \(\boldsymbol{\mu}_{f,i} (R)\) in a power series about the equilibrium geometry of the initial electronic state (since this geometry is characteristic of the molecular structure prior to photon absorption and, because the photon absorption takes place quickly, the nuclei don’t have time to move far from there):
\[\boldsymbol{\mu}_{f,i}(R) = \boldsymbol{\mu}_{f,i}(R_e) + \sum_a \frac{\partial \boldsymbol{\mu}_{f,i}}{∂R_a} (R_a - R_{a,e}) + ....\]
The first term in this expansion, when substituted into the integral over the vibrational coordinates, gives \(\boldsymbol{\mu}_{f,i}(R_e) \langle \chi_{v_f} | \chi_{v_i}\rangle \), which has the form of the electronic transition dipole multiplied by the overlap integral between the initial and final vibrational wave functions. The \(\boldsymbol{\mu}_{f,i}(R_e)\) factor was discussed above; it is the electronic transition integral evaluated at the equilibrium geometry of the absorbing state. Symmetry can often be used to determine whether this integral vanishes, as a result of which the transition will be forbidden.
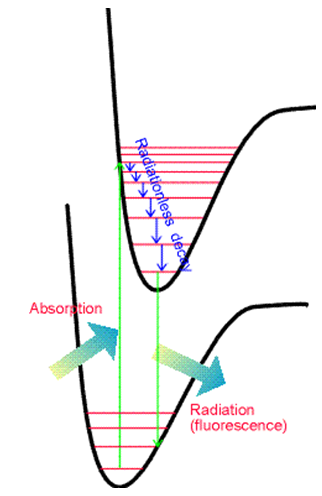
The vibrational overlap integrals \(\langle \chi_{v_f} | \chi_{v_i}\rangle \) do not necessarily vanish because \(\chi_{v_f}\) and \(\chi_{v_i}\) are eigenfunctions of different vibrational Hamiltonians because they belong to different Born-Oppenheimer energy surfaces. \(\chi_{v_f}\) is an eigenfunction whose potential energy is the final electronic state's energy surface; \(\chi_{v_i}\) has the initial electronic state's energy surface as its potential. The squares of these \(\langle \chi_{v_f} | \chi_{v_i}\rangle \) integrals, which are what eventually enter into the transition rate expression \(R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2\), are called Franck-Condon factors. Their relative magnitudes play strong roles in determining the relative intensities of various vibrational bands (i.e., series of peaks) within a particular electronic transition's spectrum. In Figure 6.16, I show two potential energy curves and illustrate the kinds of absorption (and emission) transitions that can occur when the two electronic states have significantly different geometries.
Whenever an electronic transition causes a large change in the geometry (bond lengths or angles) of the molecule, the Franck-Condon factors tend to display the characteristic broad progression shown in Figure 6.17 when considered for one initial-state vibrational level \(v_i\) and various final-state vibrational levels \(v_f\):
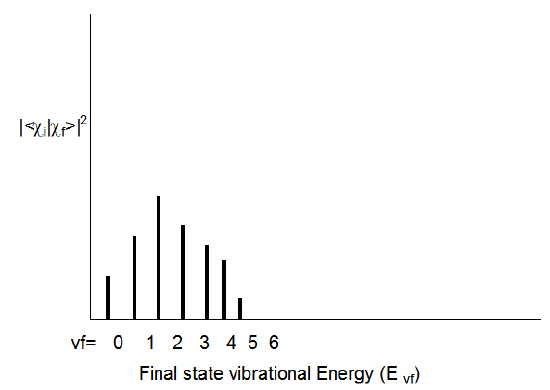
Notice that as one moves to higher \(v_f\) values, the energy spacing between the states (Evf - Evf-1) decreases; this, of course, reflects the anharmonicity in the excited-state vibrational potential. For the above example, the transition to the \(v_f = 2\) state has the largest Franck-Condon factor. This means that the overlap of the initial state's vibrational wave function \(\chi_{v_i}\) is largest for the final state's \(\chi_{v_f}\) function with \(v_f = 2\).
As a qualitative rule of thumb, the larger the geometry difference between the initial- and final- state potentials, the broader will be the Franck-Condon profile (as shown in Figure 6.17) and the larger the \(v_f\) value for which this profile peaks. Differences in harmonic frequencies between the two states can also broaden the Franck-Condon profile.
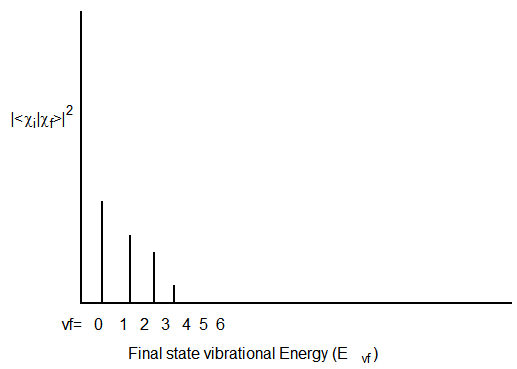
If the initial and final states have very similar geometries and frequencies along the mode that is excited when the particular electronic excitation is realized, the type of Franck-Condon profile shown in Figure 6.18 may result:
Another feature that is important to emphasize is the relation between absorption and emission when the two states’ energy surfaces have different equilibrium geometries or frequencies. Subsequent to photon absorption to form an excited electronic state but prior to photon emission, the molecule can undergoe collisions with other nearby molecules. This, of course, is especially true in condensed-phase experiments. These collisions cause the excited molecule to lose some of its vibrational and rotational energy, thereby relaxing it to lower levels on the excited electronic surface. This relaxation process is illustrated in Figure 6.19.
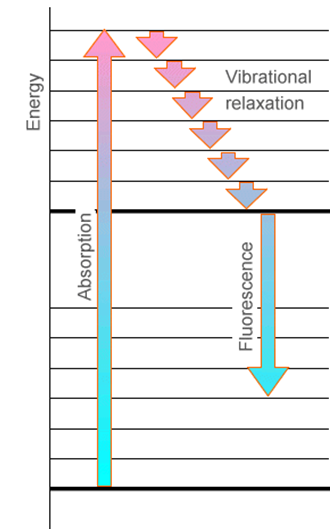
Subsequently, the electronically excited molecule can undergo photon emission (also called fluorescence) to return to its ground electronic state as shown in Figure 6.20.
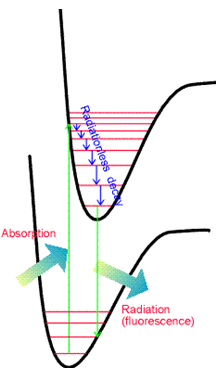
The Franck-Condon principle discussed earlier also governs the relative intensities of the various vibrational transitions arising in such emission processes. Thus, one again observes a set of peaks in the emission spectrum as shown in Figure 6.21.
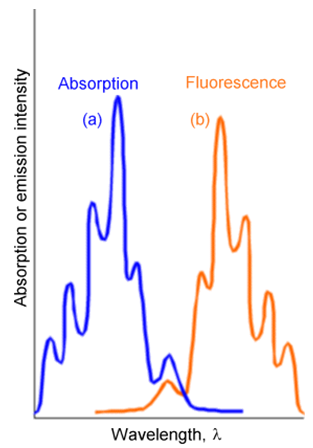
There are two differences between the lines that occur in emission and in absorption. First, the emission lines are shifted to the red (i.e., to lower energy or longer wavelength) because they occur at transition energies connecting the lowest vibrational level of the upper electronic state to various levels of the lower state. In contrast, the absorption lines connect the lowest vibrational level of the ground state to various levels of the upper state. These relationships are shown in Figure 6.22.
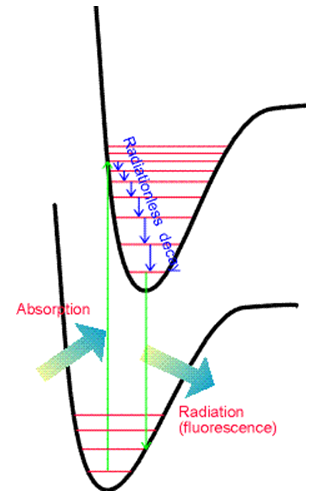
The second difference relates to the spacings among the vibrational lines. In emission, these spacings reflect the energy spacings between vibrational levels of the ground state, whereas in absorption they reflect spacings between vibrational levels of the upper state.
The above examples illustrate how vibrationally-resolved visible-UV absorption and emission spectra can be used to gain valuable information about
- the vibrational energy level spacings of the upper and ground electronic states (these spacings, in turn, reflect the strengths of the bonds existing in these states),
- the change in geometry accompanying the ground-to-excited state electronic transition as reflected in the breadth of the Franck-Condon profiles (these changes also tell us about the bonding changes that occur as the electronic transition occurs).
So, again we see how visible-UV spectroscopy can be used to learn about the electronic structure of molecules in various electronic states.
Time Correlation Function Expressions for Transition Rates
The above so-called golden-rule expression for the rates of photon-induced transitions are written in terms of the initial and final electronic/vibrational/rotational states of the molecule. There are situations in which these states simply cannot be reliably known. For example, the higher vibrational states of a large polyatomic molecule or the states of a molecule that strongly interacts with surrounding solvent molecules are such cases. In such circumstances, it is possible to recast the golden rule formula into a form that is more amenable to introducing specific physical models that lead to additional insights.
Specifically, by using so-called equilibrium averaged time correlation functions, it is possible to obtain rate expressions appropriate to a large number of molecules that exist in a distribution of initial states (e.g., for molecules that occupy many possible rotational and perhaps several vibrational levels at room temperature). As we will soon see, taking this route to expressing spectroscopic transition rates also allows us to avoid having to know each vibrational-rotational wave function of the two electronic states involved; as noted above, this is especially useful for large molecules or molecules in condensed media where such knowledge is likely not available.
To begin re-expressing the spectroscopic transition rates, the expression obtained earlier
\[R_{i,f} = \frac{2\pi}{\hbar^2} f(\omega_{f,i}) | \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle |^2 ,\]
appropriate to transitions between a particular initial state \(\Phi_i\) and a specific final state \(\Phi_f\), is rewritten as
\[R_{i,f} = \frac{2\pi}{\hbar^2} \int f(\omega)|\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \delta(\omega_{f,i}-\omega)d\omega .\]
Here, the \(\delta(\omega_{f,i} - \omega)\) function is used to specifically enforce the resonance condition which states that the photons' frequency \(\omega\) must be resonant with the transition frequency \(\omega_{f,i}\). The following integral identity can be used to replace the \(d\)-function:
\[\delta(\omega_{f,i} - \omega) = \frac{1}{\pi} \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt \]
by a form that is more amenable to further development. Then, the state-to-state rate of transition becomes:
\[R_{i,f} = \frac{1}{\hbar^2} \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega .\]
If this expression is then multiplied by the equilibrium probability \(\rho_i\) that the molecule is found in the state \(\Phi_i\) and summed over all such initial states and summed over all final states \(\Phi_f\) that can be reached from \(\Phi_i\) with photons of energy \(\hbar\omega\), the equilibrium averaged rate of photon absorption by the molecular sample is obtained:
\[R_{\rm eq.ave.} = \frac{1}{\hbar^2}\sum_{f,i} \rho_i \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega.\]
This expression is appropriate for an ensemble of molecules that can be in various initial states \(\Phi_i\) with probabilities \(\rho_i\). The corresponding result for transitions that originate in a particular state (\(\Phi_i\)) but end up in any of the allowed (by energy and selection rules) final states reads:
\[R_i = \frac{1}{\hbar^2}\sum_{f} \rho_i \int f(\omega) |\textbf{E}_0 \cdot \langle \Phi_f | \boldsymbol{\mu} | \Phi_i \rangle |^2 \int_{-\infty}^\infty \exp[i(\omega_{f,i}-\omega)t] dt d\omega.\]
As we discuss in Chapter 7, for an ensemble in which the number of molecules, the temperature \(T\), and the system volume are specified, \(\rho_i\) takes the form:
\[\rho_i = g_i \exp(-E_i^0/kT)/Q\]
where \(Q\) is the partition function of the molecules and \(g_i\) is the degeneracy of the state \(\Phi_i\) whose energy is \(E_i^0\). If you are unfamiliar with partition functions and do not want to simply trust me in the analysis of time correlation functions that we am about to undertake, I suggest you interrupt your study of Chapter 6 and read up through Section 7.1.3 of Chapter 7 at this time.
In the above expression for \(R_{\rm eq.ave.}\), a double sum occurs. Writing out the elements that appear in this sum in detail, one finds:
\[\sum_{i,f} \rho_i \textbf{E}_0· \langle \Phi_i | \boldsymbol{\mu} | \Phi_f\rangle \textbf{E}_0· \langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle \exp[i(\omega_{f,i})t].\]
In situations in which one is interested in developing an expression for the intensity arising from transitions to all allowed final states, the sum over the final states can be carried out explicitly by first writing
\[\langle \Phi_f | \boldsymbol{\mu} | \Phi_i\rangle \exp[i(\omega_{f,i})t] = \langle \Phi_f |\exp(iHt/\hbar) \boldsymbol{\mu} \exp(-iHt/\hbar)| \Phi_i\rangle \]
and then using the fact that the set of states {\(\Phi_k\)} are complete and hence obey
\[\sum_k |\Phi_k\rangle \langle \Phi_k| = 1.\]
The result of using these identities as well as the Heisenberg definition of the time-dependence of the dipole operator
\[\boldsymbol{\mu}(t) = \exp(iHt/\hbar) \boldsymbol{\mu} \exp(-iHt/\hbar),\]
is:
\[\sum_i\rho_i \langle \Phi_i | \textbf{E}_0· \boldsymbol{\mu} \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle .\]
In this form, one says that the time dependence has been reduce to that of an equilibrium averaged (i.e., as reflected in the \(\sum_i \rho_i \langle \Phi_i | | \Phi_i\rangle \) expression) time correlation function involving the component of the dipole operator along the external electric field at \(t = 0\), \(( \textbf{E}_0· \boldsymbol{\mu} )\) and this component at a different time \(t\), \((\textbf{E}_0· \boldsymbol{\mu} (t))\).
If \(\omega_{f,i}\) is positive (i.e., in the photon absorption case), the above expression will yield a non-zero contribution when multiplied by \(\exp(-i\omega t)\) and integrated over positive \(\omega\)- values. If \(\omega_{f,i}\) is negative (as for stimulated photon emission), this expression will contribute, when multiplied by \(\exp(-i\omega t)\), for negative \(\omega\)-values. In the latter situation, \(\rho_i\) is the equilibrium probability of finding the molecule in the (excited) state from which emission will occur; this probability can be related to that of the lower state \(\rho_f\) by
\[\begin{align*} \rho_{\rm excited} &= \rho_{\rm lower} \exp[ - (E^0_{\rm excited} - E^0_{\rm lower})/kT ] \\[4pt] &= \rho_{\rm lower} \exp[ - \hbar\omega/kT ]. \end{align*}\]
The absorption and emission cases can be combined into a single expression for the net rate of photon absorption by recognizing that the latter process leads to photon production, and thus must be entered with a negative sign. The resultant expression for the net rate of decrease of photons is:
\[R_{\rm eq.ave.net} = \frac{1}{\hbar^2} \sum_i \rho_i\]
\[\int \int f(\omega) \langle \Phi_i | (\textbf{E}_0· \boldsymbol{\mu}) \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle (1 - \exp(- \hbar\omega/kT) ) \exp(-i\omega t) d\omega dt.\]
It is convention to introduce the so-called line shape function \(I (\omega)\):
\[I (\omega) = \sum_i \rho_i \exp(-i\omega t) dt\]
in terms of which the net photon absorption rate is
\[R_{\rm eq.ave.net} = \frac{1}{\hbar^2} (1 - \exp(- \hbar\omega/kT) ) .\]
The function
\[C (t) = \sum_i \rho_i \langle \Phi_i | (\textbf{E}_0· \boldsymbol{\mu} ) \textbf{E}_0· \boldsymbol{\mu} (t) | \Phi_i\rangle \]
is called the equilibrium averaged time correlation function of the component of the electric dipole operator along the direction of the external electric field \(E_0\). Its Fourier transform is \(I (\omega)\), the spectral line shape function. The convolution of \(I(\omega)\) with the light source's \(f (\omega)\) function, multiplied by \((1 - \exp(-\hbar\omega/kT)\)), the correction for stimulated photon emission, gives the net rate of photon absorption.
Although the correlation function expression for the photon absorption rate is equivalent to the state-to-state expression from which it was derived, we notice that
- \(C(t)\) does not contain explicit reference to the final-state wave functions \(\phi\); instead,
- \(C(t)\) requires us to describe how the dipole operator changes with time.
That is, in the time correlation framework, one is allowed to use models of the time evolution of the system to describe the spectra. This is especially appealing for large complex molecules and molecules in condensed media because, for such systems, it would be hopeless to attempt to find the final-state wave functions, but it may be reasonable (albeit challenging) to model the system’s time evolution. Prof. Eric Heller at Harvard has pioneered the use of time-domain methods for treating molecular spectroscopy; his web site offers access to further information and insight into this subject.
It turns out that a very wide variety of spectroscopic and thermodynamic properties (e.g., light scattering intensities, diffusion coefficients, and thermal conductivity) can be expressed in terms of molecular time correlation functions. The text Statistical Mechanics, D. A. McQuarrie, Harper and Row, New York (1977) has a good treatment of many of these cases. Let’s now examine how such time evolution issues are used within the correlation function framework for the specific photon absorption case.
Line Broadening Mechanisms
If the rotational motion of the system’s molecules is assumed to be entirely unhindered (e.g., by any environment or by collisions with other molecules), it is appropriate to express the time dependence of each of the dipole time correlation functions listed above in terms of a free rotation model. For example, when dealing with diatomic molecules, the electronic-vibrational-rotational \(C(t)\) appropriate to a specific electronic-vibrational transition becomes:
\[C(t) = (q_r q_v q_e q_t)^{-1} \sum_J (2J+1) \exp\bigg(- \frac{\hbar^2J(J+1)}{8\pi^2IkT}\bigg) \exp\Big(- \frac{\hbar\nu_{\rm vib}v_i}{kT}\Big)\]
\[g_{ie} \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle |\langle \chi_{iv} | \chi_{fv}\rangle |^2\]
\[\exp(i [\hbar\nu_{\rm vib}] t + i\Delta E_{i,f} t/\hbar).\]
Here,
\[q_r = \frac{8\pi^2IkT}{\hbar^2}\]
is the rotational partition function (I being the molecule's moment of inertia \(I = mR_e^2\), and \(\dfrac{\hbar^2J(J+1)}{8\pi^2I}\) being the molecule's rotational energy for the state with quantum number \(J\) and degeneracy \(2J+1\)),
\[q_v = \frac{\exp(-\hbar\nu_{\rm vib}/2kT)}{1-\exp(-\hbar\nu_{\rm vib}/kT)}\]
is the vibrational partition function \(\nu_{\rm vib}\) being the vibrational frequency), \(g_{ie}\) is the degeneracy of the initial electronic state,
\[q_t = (2\pi mkT/\hbar^2)^{3/2} V\]
is the translational partition function for the molecules of mass \(\boldsymbol{\mu}\) moving in volume \(V\), and \(\Delta E_{i,f}\) is the adiabatic electronic energy spacing. The origins of such partition functions are treated in Chapter 7 of this text.
The functions \(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) describe the time evolution of the electronic transition dipole vector for the rotational state \(J\). In a free-rotation model, this function is taken to be of the form:
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \]
\[= \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) |\phi_J\rangle \cos(\omega_Jt)\]
where \(\omega_J\) is the rotational frequency (in cycles per second) for rotation of the molecule in the state labeled by \(J\). This oscillatory time dependence, combined with the \(\exp(i [\hbar\nu_{\rm vib}] t + i\Delta E_{i,f} t/\hbar)\) time dependence arising from the electronic and vibrational factors, produce, when this \(C(t)\) function is Fourier transformed to generate \(I(\omega)\), a series of \(d\)-function peaks. The intensities of these peaks are governed by the quantities
\[(q_r q_v q_e q_t)^{-1} \sum_J (2J+1) \exp\bigg(- \frac{\hbar^2J(J+1)}{8\pi^2IkT}\bigg) \exp\Big(- \frac{\hbar\nu_{\rm vib}v_i}{kT}\Big) g_{ie},\]
Boltzmann population factors, as well as by the \(|\langle \chi_{iv} | \chi_{fv}\rangle |^2\) Franck-Condon factors and the \(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \) terms.
This same analysis can be applied to the pure rotation and vibration-rotation \(C(t)\) time dependences with analogous results. In the former, \(d\)-function peaks are predicted to occur at
\[\omega = ± \omega_J\]
and in the latter at
\[\omega = \omega_{fv,iv} ± \omega_J ;\]
with the intensities governed by the time independent factors in the corresponding expressions for \(C(t)\).
In experimental measurements, such sharp \(d\)-function peaks are, of course, not observed. Even when very narrow bandwidth laser light sources are used (i.e., for which \(f(\omega)\) is an extremely narrowly peaked function), spectral lines are found to possess finite widths. Let us now discuss several sources of line broadening, some of which will relate to deviations from the "unhindered" rotational motion model introduced above.
Doppler Broadening
In the above expressions for \(C(t)\), the averaging over initial rotational, vibrational, and electronic states is explicitly shown. There is also an average over the translational motion implicit in all of these expressions. Its role has not (yet) been emphasized because the molecular energy levels, whose spacings yield the characteristic frequencies at which light can be absorbed or emitted, do not depend on translational motion. However, the frequency of the electromagnetic field experienced by moving molecules does depend on the velocities of the molecules, so this issue must now be addressed.
Elementary physics classes express the so-called Doppler shift of a wave's frequency induced by relative movement of the light source and the molecule as follows:
\[\omega_{\rm observed} = \omega_{\rm nominal} (1 + v_z/c)^{-1} \approx \omega_{\rm nominal} (1 - v_z/c + ...).\]
Here, \(\omega_{\rm nominal}\) is the frequency of the unmoving light source seen by unmoving molecules, \(v_z\) is the velocity of relative motion of the light source and molecules, \(c\) is the speed of light, and wobserved is the Doppler-shifted frequency (i.e., the frequency seen by the molecules). The second identity is obtained by expanding, in a power series, the \((1 + v_z/c)^{-1}\) factor, and is valid in truncated form when the molecules are moving with speeds significantly below the speed of light.
For all of the cases considered earlier, a \(C(t)\) function is subjected to Fourier transformation to obtain a spectral line shape function \(I(\omega)\), which then provides the essential ingredient for computing the net rate of photon absorption. In this Fourier transform process, the variable \(\omega\) is assumed to be the frequency of the electromagnetic field experienced by the molecules. The above considerations of Doppler shifting then lead one to realize that the correct functional form to use in converting \(C(t)\) to \(I(\omega)\) is:
\[I(\omega) = \int C(t) \exp\left(-i t \omega\Big(1-\dfrac{v_z}{c}\Big)\right)dt,\]
where \(\omega\) is the nominal frequency of the light source.
As stated earlier, within \(C(t)\) there is also an equilibrium average over translational motion of the molecules. For a gas-phase sample undergoing random collisions and at thermal equilibrium, this average is characterized by the well-known Maxwell-Boltzmann velocity distribution:
\[\left(\frac{m}{2\pi kT}\right)^{3/2} \exp\bigg(-\frac{m (v_x^2+v_y^2+v_z^2)}{2kT}\bigg) dv_x dv_y dv_z.\]
Here \(\boldsymbol{\mu}\) is the mass of the molecules and \(v_x\), \(v_y\), and \(v_z\) label the velocities along the lab-fixed Cartesian coordinates.
Defining the \(z\)-axis as the direction of propagation of the light's photons and carrying out the averaging of the Doppler factor over such a velocity distribution, one obtains:
\[\int_{-\infty}^\infty \exp\left(-i t \omega\Big(1-\dfrac{v_z}{c}\Big)\right) \left(\frac{m}{2\pi kT}\right)^{3/2}\exp\bigg(-\frac{m (v_x^2+v_y^2+v_z^2)}{2kT}\bigg) dv_x dv_y dv_z\\
= \exp(-i\omega t)\int_{-\infty}^\infty \left(\frac{m}{2\pi kT}\right)^{1/2} \exp\left(it\omega \dfrac{v_z}{c}\right)\exp\Big(-\dfrac{mv_z^2}{2kT}\Big)dv_z\]
\[= \exp(-i\omega t) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg).\]
This result, when substituted into the expressions for \(C(t)\), yields expressions identical to those given for the three cases treated above but with one modification. The translational motion average need no longer be considered in each \(C(t)\); instead, the earlier expressions for \(C(t)\) must each be multiplied by a factor \(\exp(- \omega^2t^2kT/(2mc^2))\) that embodies the translationaly averaged Doppler shift. The spectral line shape function \(I(\omega)\) can then be obtained for each \(C(t)\) by simply Fourier transforming:
\[I(\omega) = \int_{-\infty}^\infty \exp(-i\omega t)C(t) dt.\]
When applied to the rotation, vibration-rotation, or electronic-vibration-rotation cases within the unhindered rotation model treated earlier, the Fourier transform involves integrals of the form:
This integral would arise in the electronic-vibration-rotation case; the other two cases would involve integrals of the same form but with the \(\Delta E_{i,f}/\hbar\) absent in the vibration-rotation situation and with \(\omega_{fv,iv} + \Delta E_{i,f}/\hbar\) missing for pure rotation transitions. All such integrals can be carried out analytically and yield:
\[\sqrt{\frac{2mc^2\pi}{\omega^2kT}} \exp\left[ - \frac{(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2 mc^2}{2\omega^2kT} \right].\]
The result is a series of Gaussian peaks in \(\omega\)-space, centered at:
\[\omega = \omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J\]
with widths (\(\sigma\)) determined by
\[\sigma^2= \frac{\omega^2kT}{mc^2},\]
given the temperature \(T\) and the mass of the molecules \(m\). The hotter the sample, the faster the molecules are moving on average, and the broader is the distribution of Doppler shifted frequencies experienced by these molecules. The net result then of the Doppler effect is to produce a line shape function that is similar to the unhindered rotation model's series of \(d\)-functions but with each \(d\)-function peak broadened into a Gaussian shape.
If spectra can be obtained to accuracy sufficient to determine the Doppler width of the spectral lines, such knowledge can be used to estimate the temperature of the system. This can be useful when dealing with systems that cannot be subjected to alternative temperature measurements. For example, the temperatures of stars can be estimated (if their velocity relative to the earth is known) by determining the Doppler shifts of emission lines from them. Alternatively, the relative speed of a star from the earth may be determined if its temperature is known. As another example, the temperature of hot gases produced in an explosion can be probed by measuring Doppler widths of absorption or emission lines arising from molecules in these gases.
Pressure Broadening
To include the effects of collisions on the rotational motion part of any of the above \(C(t)\) functions, one must introduce a model for how such collisions change the dipole-related vectors that enter into \(C(t)\). The most elementary model used to address collisions applies to gaseous samples which are assumed to undergo unhindered rotational motion until struck by another molecule at which time a kick is applied to the dipole vector and after which the molecule returns to its unhindered rotational movement.
The effects of such infrequent collision-induced kicks are treated within the so-called pressure broadening (sometimes called collisional broadening) model by modifying the free-rotation correlation function through the introduction of an exponential damping factor \(\exp( -|t|/t)\):
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \cos \frac{\hbar J(J+1) t}{4\pi I}\]
\[Þ \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \cos \frac{\hbar J(J+1) t}{4\pi I} \exp\bigg(-\dfrac{|t|}{\tau}\bigg).\]
This damping function's time scale parameter \(\tau\) is assumed to characterize the average time between collisions and thus should be inversely proportional to the collision frequency. Its magnitude is also related to the effectiveness with which collisions cause the dipole function to deviate from its unhindered rotational motion (i.e., related to the collision strength). In effect, the exponential damping causes the time correlation function \(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) to lose its memory and to decay to zero. This memory point of view is based on viewing \(\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \) as the projection of \(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t)\) along its \(t = 0\) value \(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0)\) as a function of time t.
Introducing this additional \(\exp( -|t|/t)\) time dependence into \(C(t)\) produces, when \(C(t)\) is Fourier transformed to generate \(I(\omega)\), integrals of the form
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} ± \omega_J\Big) t \right) dt\]
In the limit of very small Doppler broadening, the \(\dfrac{\omega^2t^2kT}{2mc^2}\) factor can be ignored (i.e., \(\exp\bigg(- \dfrac{\omega^2t^2kT}{2mc^2}\bigg) \) set equal to unity), and
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
results. This integral can be performed analytically and generates:
\[\frac{1}{4\pi}\left[\frac{1/\tau}{(1/\tau)^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{1/\tau}{(1/\tau)^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right],\]
a pair of Lorentzian peaks in \(\omega\)-space centered again at
\[\omega = ± [\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J].\]
The full width at half height of these Lorentzian peaks is \(2/\tau\). One says that the individual peaks have been pressure or collisionally broadened.
When the Doppler broadening can not be neglected relative to the collisional broadening, the above integral
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
is more difficult to perform. Nevertheless, it can be carried out and again produces a series of peaks centered at
\[\omega = \omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J\]
but whose widths are determined both by Doppler and pressure broadening effects. The resultant line shapes are thus no longer purely Lorentzian nor Gaussian (which are compared in Figure 6.23 for both functions having the same full width at half height and the same integrated area), but have a shape that is called a Voight shape.
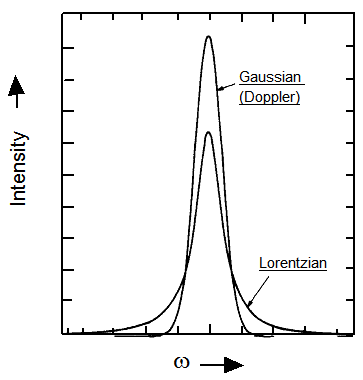
Experimental measurements of line widths that allow one to extract widths originating from collisional broadening provide information (through \(\tau\)) on the frequency of collisions and the strength of these collisions. By determining \(\tau\) at a series of gas densities, one can separate the collision-frequency dependence and determine the strength of the individual collisions (meaning how effective each collision is in reorienting the molecule’s dipole vector).
Rotational Diffusion Broadening
Molecules in liquids and very dense gases undergo such frequent collisions with the other molecules that the mean time between collisions is short compared to the rotational period for their unhindered rotation. As a result, the time dependence of the dipole-related correlation functions can no longer be modeled in terms of free rotation that is interrupted by (infrequent) collisions and Doppler shifted. Instead, a model that describes the incessant buffeting of the molecule's dipole by surrounding molecules becomes appropriate. For liquid samples in which these frequent collisions cause the dipole to undergo angular motions that cover all angles (i.e., in contrast to a frozen glass or solid in which the molecule's dipole would undergo strongly perturbed pendular motion about some favored orientation), the so-called rotational diffusion model is often used.
In this picture, the rotation-dependent part of \(C(t)\) is expressed as:
\[\langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t) |\phi_J\rangle \]
\[= \langle \phi_J | \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e) \textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,0) |\phi_J\rangle \exp( -2D_{\rm rot}|t|),\]
where \(D_{\rm rot}\) is the rotational diffusion constant whose magnitude details the time
decay in the averaged value of \(\textbf{E}_0· \boldsymbol{\mu}_{i,f}(R_e,t)\) at time \(t\) with respect to its value at time \(t = 0\); the larger \(D_{\rm rot}\), the faster is this decay. As with pressure broadening, this exponential time dependence, when subjected to Fourier transformation, yields:
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp( -2D_{\rm rot}|t|) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right)\]
Again, in the limit of very small Doppler broadening, the \(\dfrac{\omega^2t^2kT}{2mc^2}\) factor can be ignored (i.e., \(\exp\bigg(- \dfrac{\omega^2t^2kT}{2mc^2}\bigg)\) set equal to unity), and
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp( -2D_{\rm rot}|t|) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right)\]
results. This integral can be evaluated analytically and generates:
\[\frac{1}{4\pi}\left[\frac{2D_{\rm rot}}{(2D_{\rm rot})^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{2D_{\rm rot}}{(2D_{\rm rot})^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right],\]
a pair of Lorentzian peaks in \(\omega\)-space centered again at
\[\omega = ±[\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J].\]
The full width at half height of these Lorentzian peaks is \(4D_{\rm rot}\). In this case, one says that the individual peaks have been broadened via rotational diffusion. In such cases, experimental measurement of line widths yield valuable information about how fast the molecule is rotationally diffusing in its condensed environment.
Lifetime or Heisenberg Homogeneous Broadening
Whenever the absorbing species undergoes one or more processes that depletes its numbers, we say that it has a finite lifetime. For example, a species that undergoes unimolecular dissociation has a finite lifetime, as does an excited state of a molecule that decays by spontaneous emission of a photon. Any process that depletes the absorbing species contributes another source of time dependence for the dipole time correlation functions \(C(t)\) discussed above. This time dependence is usually modeled by appending, in a multiplicative manner, a factor \(\exp(-|t|/t)\). This, in turn modifies the line shape function \(I(\omega)\) in a manner much like that discussed when treating the rotational diffusion case:
\[\int_{-\infty}^\infty \exp(-i\omega t) \exp\bigg(-\dfrac{|t|}{\tau}\bigg) \exp\bigg(- \frac{\omega^2t^2kT}{2mc^2}\bigg) \exp\left(i \Big(\omega_{fv,iv} + \dfrac{\Delta E_{i,f}}{\hbar} \pm \omega_J\Big) t \right) dt\]
Not surprisingly, when the Doppler contribution is small, one obtains:
\[\frac{1}{4\pi}\left[\frac{1/\tau}{(1/\tau)^2+(\omega-\omega_{fv,iv} - \Delta E_{i,f}/\hbar ± \omega_J)^2} + \frac{1/\tau}{(1/\tau)^2+(\omega+\omega_{fv,iv} + \Delta E_{i,f}/\hbar ± \omega_J)^2} \right].\]
In these Lorentzian lines, the parameter \(\tau\) describes the kinetic decay lifetime of the molecule. One says that the spectral lines have been lifetime or Heisenberg broadened by an amount proportional to \(1/\tau\). The latter terminology arises because the finite lifetime of the molecular states can be viewed as producing, via the Heisenberg uncertainty relation \(\Delta E \Delta t \rangle \hbar\), states whose energy is uncertain to within an amount \(\Delta E\).
Site Inhomogeneous Broadening
Among the above line broadening mechanisms, the pressure, rotational diffusion, and lifetime broadenings are all of the homogeneous variety. This means that each and every molecule in the sample is affected in exactly the same manner by the broadening process. For example, one does not find some molecules with short lifetimes and others with long lifetimes in the Heisenberg case; the entire ensemble of molecules is characterized by a single lifetime.
In contrast, Doppler broadening is inhomogeneous in nature because each molecule experiences a broadening that is characteristic of its particular velocity \(v_z\). That is, the fast molecules have their lines broadened more than do the slower molecules. Another important example of inhomogeneous broadening is provided by so-called site broadening. Molecules imbedded in a liquid, solid, or glass do not, at the instant of their photon absorption, all experience exactly the same interactions with their surroundings. The distribution of instantaneous solvation environments may be rather narrow (e.g., in a highly ordered solid matrix) or quite broad (e.g., in a liquid at high temperature or in a super-critical liquid). Different environments produce different energy level splittings \(\omega = \omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J\) (because the initial and final states are solvated differently by the surroundings) and thus different frequencies at which photon absorption can occur. The distribution of energy level splittings causes the sample to absorb at a range of frequencies as illustrated in Figure 6.24 where homogeneous and inhomogeneous line shapes are compared.
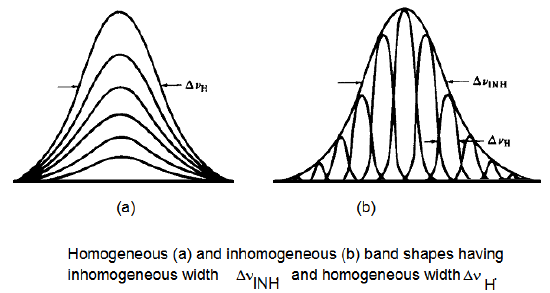
The spectral line shape function \(I(\omega)\) is therefore further broadened when site inhomogeneity is present and significant. These effects can be modeled by convolving the kind of \(I(\omega)\) function that results from Doppler, lifetime, rotational diffusion, and pressure broadening with a Gaussian distribution \(P(\Delta E)\) that describes the inhomogeneous distribution of energy level splittings:
\[I(\omega) = \int I^0(\omega,\Delta E)P(\Delta E)d\Delta E.\]
Here \(I^0(\omega;\Delta E)\) is a line shape function such as those described earlier each of which contains a set of frequencies (e.g., \(\omega_{fv,iv}+\Delta E_{i,f}/\hbar ± \omega_J +\Delta E /\hbar = \omega+\Delta E /\hbar\)) at which absorption or emission occurs and \(P(\Delta E)\) is a Gaussian probability function describing the inhomogeneous broadening of the energy splitting \(\Delta E\).
A common experimental test to determine whether inhomogeneous broadening is significant involves hole burning. In such experiments, an intense light source (often a laser) is tuned to a frequency \(\omega_{\rm burn}\) that lies within the spectral line being probed for inhomogeneous broadening. Then, with the intense light source constantly turned on, a second tunable light source is used to scan through the profile of the spectral line, and an absorption spectrum is recorded. Given an absorption profile as shown in Figure 6.25 in the absence of the intense burning light source:
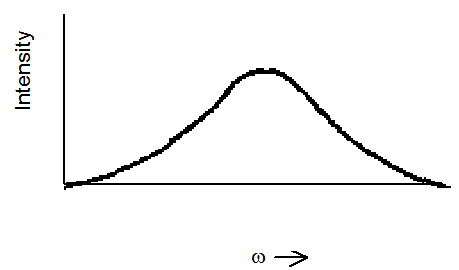
one expects to see a profile such as that shown in Figure 6.26 if inhomogeneous broadening is operative.
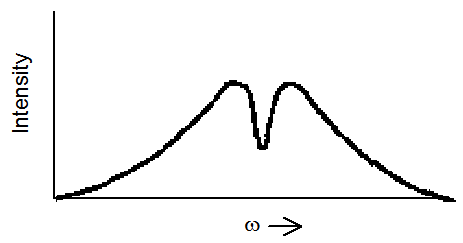
The interpretation of the change in the absorption profile caused by the bright light source proceeds as follows:
- In the ensemble of molecules contained in the sample, some molecules will absorb at or near the frequency of the bright light source \(\omega_{\rm burn}\); other molecules (those whose environments do not produce energy level splittings that match \(\omega_{\rm burn}\)) will not absorb at this frequency.
- Those molecules that do absorb at \(\omega_{\rm burn}\) will have their transition saturated by the intense light source, thereby rendering this frequency region of the line profile transparent to further absorption.
- When the probe light source is scanned over the line profile, it will induce absorptions for those molecules whose local environments did not allow them to be saturated by the \(\omega_{\rm burn}\) light. The absorption profile recorded by this probe light source's detector thus will match that of the original line profile, until
- The probe light source's frequency matches \(\omega_{\rm burn}\), upon which no absorption of the probe source's photons will be recorded because molecules that absorb in this frequency regime have had their transition saturated.
- Hence, a hole will appear in the absorption spectrum recorded by the probe light source's detector in the region of \(\omega_{\rm burn}\).
Unfortunately, the technique of hole burning does not provide a fully reliable method for identifying inhomogeneously broadened lines. If a hole is observed in such a burning experiment, this provides ample evidence, but if one is not seen, the result is not definitive. In the latter case, the transition may not be strong enough (i.e., may not have a large enough rate of photon absorption) for the intense light source to saturate the transition to the extent needed to form a hole.
Photoelectron Spectroscopy
Photoelectron spectroscopy (PES) is a special kind of electronic spectroscopy. It uses visible or UV light to excite a molecule or ion to a final state in which an electron is ejected. In effect, it induces transitions to final states in which an electron has been promoted to an unbound so-called continuum orbital. Most PES experiments are carried out using a fixed-frequency light source (usually a laser). This source’s photons, when absorbed, eject electrons whose intensity and kinetic energies \(KE\) are then measured. Subtracting the electrons’ \(KE\) from the photon’s energy \(h\nu\) gives the binding energy \(BE\) of the electron:
\[BE = h\nu - KE.\]
If the sample subjected to the PES experiment has molecules in a variety of initial states (e.g., two electronic states or various vibrational-rotational levels of the ground electronic state) having various binding energies \(BE_k\), one will observe a series of peaks corresponding to electrons ejected with a variety of kinetic energies \(KE_k\) as Figure 6.27 illustrates and as the energy-balance condition requires:
\[BE_k = h\nu - KE_k.\]
The peak of electrons detected with the highest kinetic energy came from the highest-lying state of the parent, while those with low kinetic energy came from the lowest-energy state of the parent.
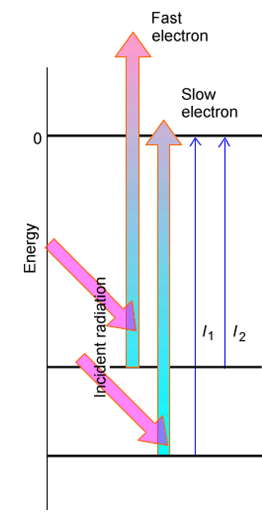
By examining the spacings between these peaks, one learns about the spacings between the energy levels of the parent species that has been subjected to electron loss.
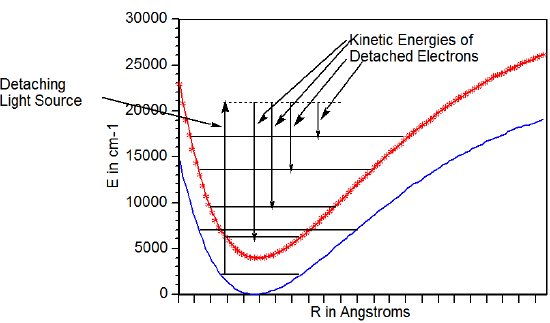
Alternatively, if the parent species exists primarily in its lowest state but the daughter species produced when an electron is removed from the parent has excited (electronic, vibration-rotation) states that can be accessed, one can observe a different progression of peaks. In this case, the electrons with highest kinetic energy arise from transitions leading to the lowest-energy state of the daughter as Figure 6.28 illustrates. In that figure, the lower energy surface belongs to the parent and the upper curve to the daughter.
An example of experimental photodetachment data is provided in Figure 6.29 showing the intensity of electrons detected when \(Cu_2^-\) anion loses an electron vs. the kinetic energy of the ejected electrons.
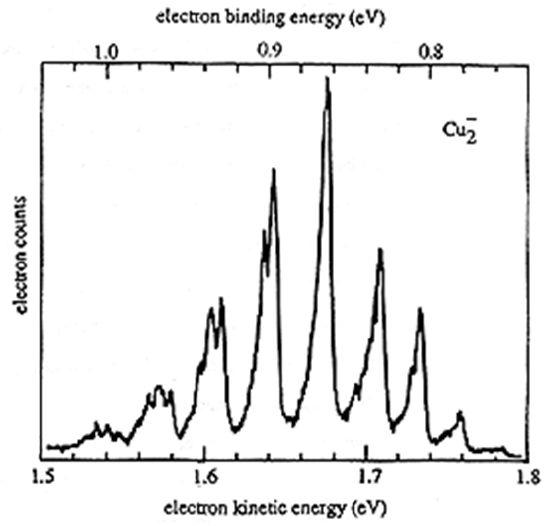
The peak at a kinetic energy of ca. 1.54 eV, corresponding to a binding energy of 1.0 eV, arises from \(Cu_2^-\) in \(v=0\) losing an electron to produce \(Cu_2\) in \(v=0\). The most intense peak corresponds to a \(v=0\) to \(v=4\) transition. As in the visible-UV spectroscopy case, Franck-Condon factors involving the overlap of the \(Cu_2^-\) anion and \(Cu_2\) neutral vibrational wave functions govern the relative intensities of the PES peaks.
Another example is given in Figure 6.30 where the photodetachment spectrum of \(H_2C=C^-\) (the anion of the carbene vinylidene) appears.
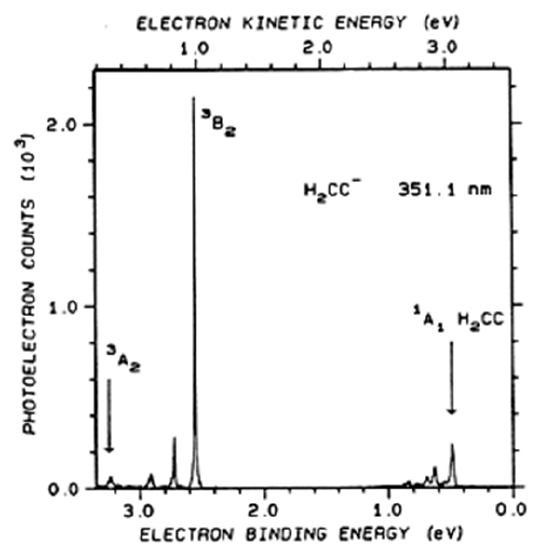
In this spectrum, the peaks having electron binding energies near 0.5 eV correspond to transitions in which ground-state \(H_2C=C^-\) in \(v=0\) is detached to produce ground-state (\(^1A_1\)) \(H_2C=C\) in various v levels. The spacings between this group of peaks relate to the spacings in vibrational states of this \(^1A_1\) electronic state. The series of peaks with binding energies near 2.5 eV correspond to transitions in which \(H_2C=C^-\) is detached to produce \(H_2C=C\) in its \(^3B_2\) excited electronic state. The spacings between peaks in this range relate to spacings in vibrational states of this \(^3B_2\) state. The spacing between the peaks near 0.5 eV and those near 2.5 eV relate to the energy difference between the \(^3B_2\) and \(^1A_1\) electronic states of the neutral \(H_2C=C\).
Because PES offers a direct way to measure energy differences between anion and neutral or neutral and cation state energies, it is a powerful and widely used means of determining molecular electron affinities (EAs) and ionization potentials (IPs). Because IPs and EAs relate, via Koopmans’ theorem, to orbital energies, PES is thus seen to be a way to measure orbital energies. Its vibrational envelopes also offer a good way to probe vibrational energy level spacings, and hence the bonding strengths.
Probing Continuum Orbitals
There is another type of spectroscopy that can be used to directly probe the orbitals of a molecule that lie in the continuum (i.e., at energies higher than that of the parent neutral). I ask that you reflect back on our discussion in Chapter 2 of tunneling and of resonance states that can occur when an electron experiences both attractive and repulsive potentials. In such cases, there exists a special energy at which the electron can be trapped by the attractive potential and have to tunnel through the repulsive barrier to eventually escape. It is these kinds of situations that this spectroscopy probes.
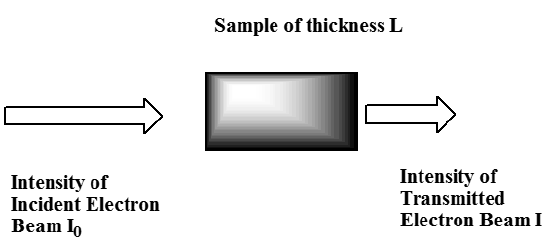
This experiment is called electron-transmission spectroscopy (ETS). In such an experiment, a beam of electrons having a known intensity \(I_0\) and narrowly defined range of kinetic energies \(E\) is allowed to pass through a sample (usually gaseous) of thickness \(L\). The intensity \(I\) of electrons observed to pass through the sample and arrive at a detector lying along the incident beam’s direction is monitored, as are the kinetic energies of these electrons \(E’\). Such an experiment is described in qualitative form in Figure 6.31.
If the molecules in the sample have a resonance orbital whose energy is close to the kinetic energy \(E\) of the colliding electrons, it is possible for an electron from the beam to be captured into such an orbital and to exist in this orbital for a considerable time. Of course, in the absence of any collisions or other processes to carry away excess energy, this anion will re-emit an electron at a later time. Hence, such anions are called metastable and their electronic states are called resonance states. If the captured electron remains in this orbital for a length of time comparable to or longer than the time it takes for the nascent molecular anion to undergo vibrational or rotational motion, various events can take place before the electron is re-emitted:
i.some bond lengths or angles can change (this will happen if the orbital occupied by the beam’s electron has bonding or antibonding character) so, when the electron is subsequently emitted, the neutral molecule is left with a change in vibrational energy;
ii.the molecule may rotate, so when the electron is ejected, it is not emitted in the same direction as the incident beam.
In the former case, one observes electrons emitted with energies \(E’\) that differ from that of the incident beam by amounts related to the internal vibrational energy levels of the anion. In the latter, one sees a reduction in the intensity of the beam that is transmitted directly through the sample and electrons that are scattered away from this direction.
Such an ETS spectrum is shown in Figure 6.32 for a gaseous sample of \(CO_2\) molecules.
In this spectrum, the energy of the transmitted beam’s electrons is plotted on the horizontal axis and the derivative of the intensity of the transmitted beam is plotted on the vertical axis. It is common to plot such derivatives in ETS-type experiments to allow the variation of the signal with energy to be more clearly identified.
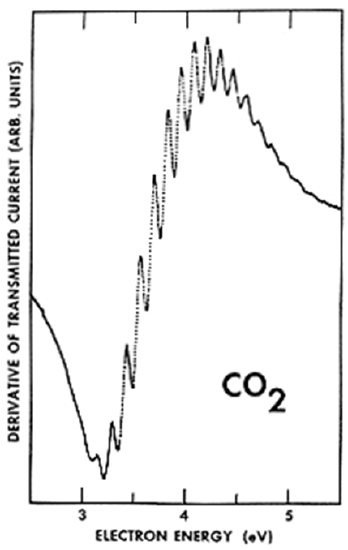
In this ETS spectrum of \(CO_2\), the oscillations that appear within the major spectral feature displayed (whose center is near 3.8 eV) correspond to stretching and bending vibrational levels of the metastable \(CO_2^-\) anion. It is the bending vibration that is primarily excited because the beam electron enters the LUMO of \(CO_2\), which is an orbital of the form shown in Figure 6.33.
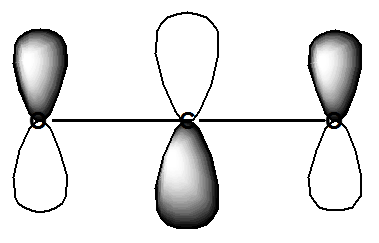
Occupancy of this antibonding \(\pi^*\) orbital, causes both C-O bonds to lengthen and the O-C-O angle to bend away from 180 deg. The bending allows the antibonding nature of this orbital to be reduced.
Other examples of ETS spectra are shown in Figure 6.34.
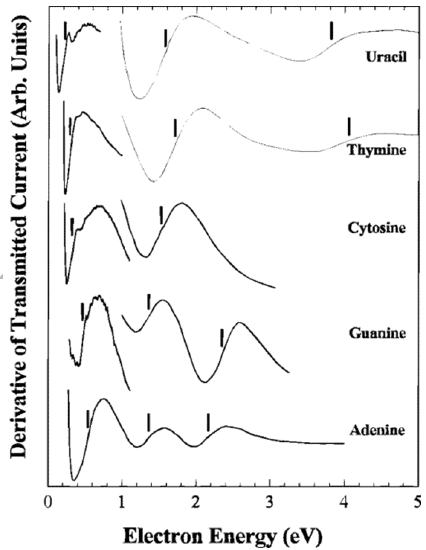
Here, again a derivative spectrum is shown, and the vertical lines have been added to show where the derivative passes through zero, which is where the ETS absorption signal would have a peak. These maxima correspond to electrons entering various virtual \(\pi^*\) orbitals of the uracil and DNA base molecules. It is by finding these peaks in the ETS spectrum that one can determine the energies of such continuum orbitals.
Before closing this section, it is important to describe how one uses theory to simulate the metastable states that arise in such ETS experiments. Such calculations are not at all straightforward, and require the introduction of special tools designed to properly model the resonant continuum orbital.
For metastable anions, it is difficult to approximate the potential experienced by the excess electron. For example, singly charged anions in which the excess electron occupies a molecular orbital \(\phi\) that possesses non-zero angular momentum have effective potentials as shown in Figure 6.35, which depend on the angular momentum \(L\) value of the orbital.
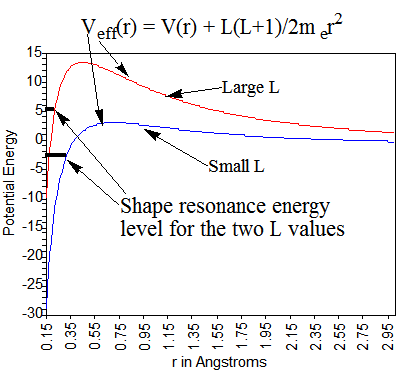
For example, the \(\pi^*\) orbital of \(N_2^-\) shown in Figure 6.36 produces two counteracting contributions to the effective radial potential \(V_{\rm eff}(r)\) experienced by an electron occupying it.
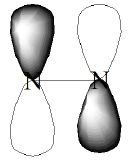
First, the two nitrogen centers exert attractive potentials on the electron in this orbital. These attractions are strongest when the excess electron is near the nuclei but decay rapidly at larger distances because the other electrons’ Coulomb repulsions screen the nuclear attractions. Secondly, because the \(\pi^*\) molecular orbital is comprised of atomic basis functions of \(p_{\pi}\), \(d_{\pi}\), etc. symmetry, it possesses non-zero angular momentum. Because the \(\pi^*\) orbital has gerade symmetry, its large-r character is dominated by \(L = 2\) angular momentum. As a result, the excess electron has a centrifugal radial potential \(L(L+1)/2m_er^2\) derived largely from its \(L = 2\) character.
The attractive short-range valence potentials \(V(r)\) and the centrifugal potential combine to produce a net effective potential as illustrated in Figure 6.35. The energy of an electron experiencing such a potential may or may not lie below the \(r \rightarrow \infty\) asymptote. If the attractive potential is sufficiently strong, as it is for \(O_2^{-1}\), the electron in the \(\pi^*\) orbital will be bound and its energy will lie below this asymptote. On the other hand, if the attractive potential is not as strong, as is the case for the less-electronegative nitrogen atoms in \(N_2^{-1}\), the energy of the \(\pi^*\) orbital can lie above the asymptote. In the latter cases, we speak of metastable shape-resonance states. They are metastable because their energies lie above the asymptote so they can decay by tunneling through the centrifugal barrier. They are called shape-resonances because their metastability arises from the shape of their repulsive centrifugal barrier.
If one had in-hand a reasonable approximation to the attractive short-range potential \(V(r)\) and if one knew the L-symmetry of the orbital occupied by the excess electron, one could form \(V_{\rm eff}(r)\) as above. However, to compute the lifetime of the shape resonance, one has to know the energy \(E\) of this state. The most common and powerful tool for studying such metastable states theoretically is the stabilization method (SM) that Prof. Howard Taylor at USC pioneered. This method involves embedding the system of interest (e.g., the \(N_2^{-1}\) anion) within a finite radial box in order to convert the continuum of states corresponding, for example, to \(N_2 + e^-\), into discrete states that can be handled using more conventional methods. By then varying the size of the box, one can vary the energies of the discrete states that correspond to \(N_2 + e^-\) (i.e., one varies the kinetic energy \(KE\) of the orbital containing the excess electron). As the box size is varied, one eventually notices (e.g., by plotting the orbitals) that one of the \(N_2 + e^-\) states possesses a significant amount of valence (i.e., short-range) character. That is, one such state has significant amplitude not only at large-r but also in the region of the two nitrogen centers. It is this state that corresponds to the metastable shape-resonance state, and it is the energy \(E\) where significant valence components develop that provides the stabilization estimate of the state energy.
Let us continue using \(N_2^{-1}\) as an example for how the SM would be employed, especially how one usually varies the box within which the anion is constrained. One would use a conventional atomic orbital basis set that would likely include s and \(\pi\) functions on each \(N\) atom, perhaps some polarization d functions and some conventional diffuse s and \(\pi\) orbitals on each \(N\) atom. These basis orbitals serve primarily to describe the motions of the electrons within the usual valence regions of space.
To this basis, one would append extra sets of diffuse \(\pi\)-symmetry orbitals. These orbitals could be \(p_\pi\) (and maybe \(d_\pi\)) functions centered on each nitrogen atom, or they could be \(p_\pi\) (and maybe \(d_\pi\)) orbitals centered at the midpoint of the N-N bond. One usually would not add just one such function; rather several such functions, each with an orbital exponent \(\alpha_J\) that characterizes its radial extent, would be used. Let us assume, for example, that \(K\) such \(\pi\) functions have been used.
Next, using the conventional atomic orbital basis as well as the \(K\) extra \(\pi\) basis functions, one carries out a calculation (most often a variational calculation in which one computes many energy levels) on the \(N_2^{-1}\) anion. In this calculation, one tabulates the energies of many (say M) of the electronic states of \(N_2^{-1}\). Of course, because a finite atomic orbital basis set must be used, one finds a discrete spectrum of orbital energies and thus of electronic state energies. There are occupied orbitals having negative energy that represent, via. Koopmans' theorem, the bound states of the \(N_2^-\). There are also so-called virtual orbitals (i.e., those orbitals that are not occupied) whose energies lie above zero (i.e., do not describe bound states). The latter orbitals offer a discrete approximation to the continuum within which the resonance state of interest lies.
One then scales the orbital exponents {\(\alpha_J\)} of the \(K\) extra \(\pi\) basis orbitals by a factor \(\eta\): \(\alpha_J \rightarrow \eta \alpha_J\) and repeats the calculation of the energies of the M lowest energies of \(N_2^{-1}\). This scaling causes the extra \(\pi\) basis orbitals to contract radially (if \(\eta > 1\)) or to expand radially (if \(\eta < 1\)). It is this basis orbital expansion and contraction that produces expansion and contraction of the box discussed above. That is, one does not employ a box directly; instead, one varies the radial extent of the most diffuse basis orbitals to simulate the box variation.
If the conventional orbital basis is adequate, one finds that the extra \(\pi\) orbitals, whose exponents are being scaled, do not affect appreciably the energy of the neutral \(N_2\) molecule. This can be probed by plotting the \(N_2\) energy as a function of the scaling parameter h; if the energy varies little with \(\eta\), the conventional basis is adequate.
In contrast to plots of the neutral \(N_2\) energy vs. \(\eta\), plots of the energies of the M \(N_2^{-1}\) states show significant h-dependence as Figure 6.37 illustrates.
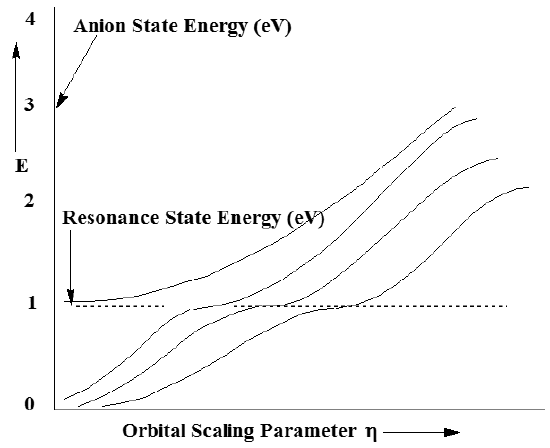
What does such a stabilization plot tell us and what do the various branches of the plot mean? First, one should notice that each of the plots of the energy of an anion state (relative to the neutral molecule’s energy, which is independent of \(\eta\)) grows with increasing h. This h-dependence arises from the h-scaling of the extra diffuse \(\pi\) basis orbitals. Because most of the amplitude of such basis orbitals lies outside the valence region, the kinetic energy is the dominant contributor to such orbitals’ energy. Because \(\eta\) enters into each orbital as \(\exp(-\eta \alpha r^2)\), and because the kinetic energy operator involves the second derivative with respect to r, the kinetic energies of orbitals dominated by the diffuse \(\pi\) basis functions vary as \(\eta^2\).
For small \(\eta\), all of the \(\pi\) diffuse basis functions have their amplitudes concentrated at large r and have low kinetic energy. This is because, for small \(\eta\) all of these orbitals are very diffuse and concentrate electron density at large distances. As \(\eta\) grows, these functions become more radially compact and their kinetic energies grow. For example, note the three lowest energies shown above increasing from near zero as \(\eta\) grows.
As \(\eta\) further increases, one reaches a point at which the third and fourth anion-state energies undergo an avoided crossing. At this \(\eta\) value, if one examines the nature of the two wave functions whose energies avoid one another, one finds that one of them contains substantial amounts of both valence and extra-diffuse \(\pi\) function character. Just to the left of the avoided crossing, the lower-energy state (the third state for small \(\eta\)) contains predominantly extra diffuse \(\pi\) orbital character, while the higher-energy state (the fourth state) contains largely valence \(\pi^*\) orbital character.
However, at the special value of \(\eta\) where these two states nearly cross, the kinetic energy of the third state (as well as its radial size and its de Broglie wavelength) are appropriate to connect properly with the fourth state. By connect properly we mean that the two states have wave function amplitudes, phases, and slopes that match. So, at this special \(\eta\) value, one can achieve a description of the shape-resonance state that correctly describes this state both in the valence region and in the large-r region. Only by tuning the energy of the large-r states using the \(\eta\) scaling can one obtain this proper boundary condition matching.
In summary, by carrying out a series of anion-state energy calculations for several states and plotting them vs. \(\eta\), one obtains a stabilization graph. By examining this graph and looking for avoided crossings, one can identify the energies at which metastable resonances occur. It is also possible to use the shapes (i.e., the magnitude of the energy splitting between the two states and the slopes of the two avoiding curves) of the avoided crossings in a stabilization graph to compute the lifetimes of the metastable states. Basically, the larger the avoided crossing energy splitting between the two states, the shorter is the lifetime of the resonance state.
So, the ETS and PES experiments offer wonderful probes of the bound and continuum states of molecules and ions that tell us a lot about the electronic nature and chemical bonding of these species. The theoretical study of these phenomena is complicated by the need to properly identify and describe any continuum orbitals and states that are involved. The stabilization technique allows us to achieve a good approximation to resonance states that lie in such continua.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


