5.1: What is Theoretical Chemistry About?
- Page ID
- 11586
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The science of chemistry deals with molecules including the radicals, cations, and anions they produce when fragmented or ionized. Chemists study isolated molecules (e.g., as occur in the atmosphere and in astronomical environments), solutions of molecules or ions dissolved in solvents, as well as solid, liquid, and plastic materials comprised of molecules. All such forms of molecular matter are what chemistry is about. Chemical science includes how to make molecules (synthesis), how to detect and quantitate them (analysis), how to probe their properties and the changes they undergo as reactions occur (physical).
Molecular Structure- bonding, shapes, electronic structures
One of the more fundamental issues chemistry addresses is molecular structure, which means how the molecule’s atoms are linked together by bonds and what the inter-atomic distances and angles are. Another component of structure analysis relates to what the electrons are doing in the molecule; that is, how the molecule’s orbitals are occupied and in which electronic state the molecule exists. For example, in the arginine molecule shown in Figure 5.1, a \(HOOC^-\) carboxylic acid group (its oxygen atoms are shown in red) is linked to an adjacent carbon atom (yellow) which itself is bonded to an \(–NH_2\) amino group (whose nitrogen atom is blue). Also connected to the a-carbon atom are a chain of three methylene \(–CH_2^-\) groups, a \(–NH^-\) group, then a carbon atom attached both by a double bond to an imine \(–NH\) group and to an amino \(–NH_2\) group.
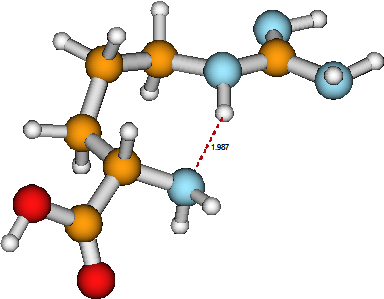
The connectivity among the atoms in arginine is dictated by the well known valence preferences displayed by H, C, O, and N atoms. The internal bond angles are, to a large extent, also determined by the valences of the constituent atoms (i.e., the \(sp_3\) or \(sp_2\) nature of the bonding orbitals). However, there are other interactions among the several functional groups in arginine that also contribute to its ultimate structure. In particular, the hydrogen bond linking the a-amino group’s nitrogen atom to the \(–NH^-\) group’s hydrogen atom causes this molecule to fold into a less extended structure than it otherwise might.
What does theory have to do with issues of molecular structure and why is knowledge of structure so important? It is important because the structure of a molecule has a very important role in determining the kinds of reactions that molecule will undergo, what kind of radiation it will absorb and emit, and to what active sites in neighboring molecules or nearby materials it will bind. A molecule’s shape (e.g., rod like, flat, globular, etc.) is one of the first things a chemist thinks of when trying to predict where, at another molecule or on a surface or at a cell membrane, the molecule will fit and be able to bind and perhaps react. The presence of lone pairs of electrons (which act as Lewis base sites), of \(\pi\) orbitals (which can act as electron donor and electron acceptor sites), and of highly polar or ionic groups guide the chemist further in determining where on the molecule’s framework various reactant species (e.g., electrophilic or nucleophilic or radical) will be most strongly attracted. Clearly, molecular structure is a crucial aspect of the chemists’ toolbox.
How does theory relate to molecular structure? As we discussed in the Part 1 of this text, the Born-Oppenheimer approximation leads us to use quantum mechanics to predict the energy \(E\) of a molecule for any positions ({\(R_a\)}) of its nuclei, given the number of electrons Ne in the molecule (or ion). This means, for example, that the energy of the arginine molecule in its lowest electronic state (i.e., with the electrons occupying the lowest energy orbitals) can be determined for any location of the nuclei if the Schrödinger equation governing the movements of the electrons can be solved.
If you have not had a good class on how quantum mechanics is used within chemistry, I urge you to take the time needed to master Part 1. In those pages, I introduce the central concepts of quantum mechanics and I show how they apply to several very important cases including
- electrons moving in 1, 2, and 3 dimensions and how these models relate to electronic structures of polyenes and to electronic bands in solids
- the classical and quantum probability densities and how they differ,
- time propagation of quantum wave functions,
- the Hückel or tight-binding model of chemical bonding among atomic orbitals,
- harmonic vibrations,
- molecular rotations,
- electron tunneling,
- atomic orbitals’ angular and radial characteristics,
- and point group symmetry and how it is used to label orbitals and vibrations
You need to know this material if you wish to understand most of what this text offers, so I urge you to read Part 1 if your education to date has not yet adequately been exposed to it.
Let us now return to the discussion of how theory deals with molecular structure. We assume that we know the energy \(E(\{R_a\})\) at various locations {\(R_a\)} of the nuclei. In some cases, we denote this energy \(V(R_a)\) and in others we use \(E(R_a)\) because, within the Born-Oppenheimer approximation, the electronic energy \(E\) serves as the potential V for the molecule’s vibrational motions. As discussed in Part 1, one can then perform a search for the lowest energy structure (e.g., by finding where the gradient vector vanishes \(\dfrac{∂E}{∂R_a}=0\) and where the second derivative or Hessian matrix \(\bigg(\dfrac{∂^2E}{∂R_a∂R_b}\bigg)\) has no negative eigenvalues). By finding such a local-minimum in the energy landscape, theory is able to determine a stable structure of such a molecule. The word stable is used to describe these structures not because they are lower in energy than all other possible arrangements of the atoms but because the curvatures, as given in terms of eigenvalues of the Hessian matrix \(\bigg(\dfrac{∂^2E}{∂R_a∂R_a}\bigg)\), are positive at this particular geometry. The procedures by which minima on the energy landscape are found may involve simply testing whether the energy decreases or increases as each geometrical coordinate is varied by a small amount. Alternatively, if the gradients \(\dfrac{∂E}{∂R_a}\) are known at a particular geometry, one can perform searches directed downhill along the negative of the gradient itself. By taking a small step along such a direction, one can move to a new geometry that is lower in energy. If not only the gradients \(\dfrac{∂E}{∂R_a}\) but also the second derivatives \(\bigg(\dfrac{∂^2E}{∂R_a∂R_a}\bigg)\) are known at some geometry, one can make a more intelligent step toward a geometry of lower energy. For additional details about how such geometry optimization searches are performed within modern computational chemistry software, see Chapter 3 where this subject was treated in greater detail.
It often turns out that a molecule has more than one stable structure (isomer) for a given electronic state. Moreover, the geometries that pertain to stable structures of excited electronic state are different than those obtained for the ground state (because the orbital occupancy and thus the nature of the bonding is different). Again using arginine as an example, its ground electronic state also has the structure shown in Figure 5.2 as a stable isomer. Notice that this isomer and that shown earlier have the atoms linked together in identical manners, but in the second structure the a-amino group is involved in two hydrogen bonds while it is involved in only one in the former. In principle, the relative energies of these two geometrical isomers can be determined by solving the electronic Schrödinger equation while placing the constituent nuclei in the locations described in the two figures.
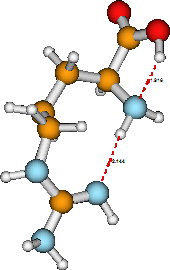
If the arginine molecule is excited to another electronic state, for example, by promoting a non-bonding electron on its C=O oxygen atom into the neighboring C-O \(\pi^*\) orbital, its stable structures will not be the same as in the ground electronic state. In particular, the corresponding C-O distance will be longer than in the ground state, but other internal geometrical parameters may also be modified (albeit probably less so than the C-O distance). Moreover, the chemical reactivity of this excited state of arginine will be different than that of the ground state because the two states have different orbitals available to react with attacking reagents.
In summary, by solving the electronic Schrödinger equation at a variety of geometries and searching for geometries where the gradient vanishes and the Hessian matrix has all positive eigenvalues, one can find stable structures of molecules (and ions). The Schrödinger equation is a necessary aspect of this process because the movement of the electrons is governed by this equation rather than by Newtonian classical equations. The information gained after carrying out such a geometry optimization process include (1) all of the inter-atomic distances and internal angles needed to specify the equilibrium geometry {\(R_{a{\rm eq}}\)} and (2) the total electronic energy \(E\) at this particular geometry.
It is also possible to extract much more information from these calculations. For example, by multiplying elements of the Hessian matrix \(\bigg(\dfrac{∂^2E}{∂R_a∂R_b}\bigg)\) by the inverse square roots of the atomic masses of the atoms labeled a and b, one forms the mass-weighted Hessian (\(\dfrac{1}{\sqrt{m_am_b}}\dfrac{∂^2E}{∂R_a∂R_b}\)) whose non-zero eigenvalues give the harmonic vibrational frequencies {\(\omega_k\)} of the molecule. The eigenvectors {\(R_{k,a}\)} of the mass-weighted Hessian matrix give the relative displacements in coordinates \(R_{ka}\) that accompany vibration in the \(k^{\rm th}\) normal mode (i.e., they describe the normal mode motions). Details about how these harmonic vibrational frequencies and normal modes are obtained were discussed earlier in Chapter 3.
Molecular Change- reactions and interactions
1.Changes in bonding
Chemistry also deals with transformations of matter including changes that occur when molecules react, are excited (electronically, vibrationally, or rotationally), or undergo geometrical rearrangements. Again, theory forms the cornerstone that allows experimental probes of chemical change to be connected to the molecular level and that allows simulations of such changes.
Molecular excitation may or may not involve altering the electronic structure of the molecule; vibrational and rotational excitation do not, but electronic excitation, ionization, and electron attachment do. As illustrated in Figure 5.3 where a bi-molecular reaction is displayed, chemical reactions involve breaking some bonds and forming others, and thus involve rearrangement of the electrons among various molecular orbitals.
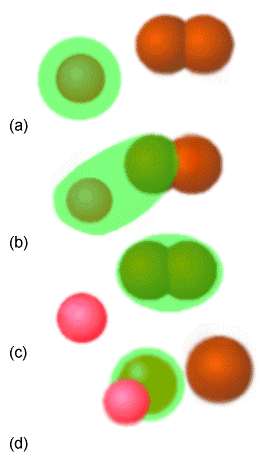
In this example, in part (a) the green atom collides with the brown diatomic molecule and forms the bound triatomic molecule (b). Alternatively, in (c) and (d), a pink atom collides with a green diatomic to break the bond between the two green atoms and form a new bond between the pink and green atoms. Both such reactions are termed bi-molecular because the basic step in which the reaction takes place requires a collision between to independent species (i.e., the atom and the diatomic).
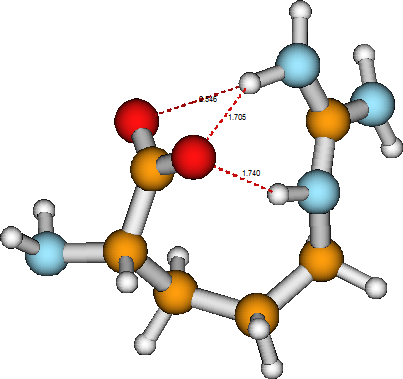
A simple example of a unimolecular chemical reaction is offered by the arginine molecule considered above. In the first structure shown for arginine, the carboxylic acid group retains its \(HOOC-\) bonding. However, in the zwitterion structure of this same molecule, shown in Figure 5.4, the \(HOOC-\) group has been deprotonated to produce a carboxylate anion group \(–COO^-\), with the \(H^+\) ion now bonded to the terminal imine group, thus converting it to an amino group and placing the net positive charge on the adjacent carbon atom. The unimolecular tautomerization reaction in which the two forms of arginine are interconverted involves breaking an \(O-H\) bond, forming a \(N-H\) bond, and changing a carbon-nitrogen double bond into a carbon-nitrogen single bond. In such a process, the electronic structure is significantly altered, and, as a result, the two isomers can display very different chemical reactivities toward other reagents. Notice that, once again, the ultimate structure of the zwitterion tautomer of arganine is determined by the valence preferences of its constituent atoms as well as by hydrogen bonds formed among various functional groups (the carboxylate group and one amino group and one \(–NH^-\) group).
Energy Conservation
In any chemical reaction as in all physical processes (other than nuclear event in which mass and energy can be interconveted), total energy must be conserved. Reactions in which the summation of the strengths of all the chemical bonds in the reactants exceeds the sum of the bond strengths in the products are termed endothermic. For such reactions, external energy must to provided to the reacting molecules to allow the reaction to occur. Exothermic reactions are those for which the bonds in the products exceed in strength those of the reactants. For exothermic reactions, no net energy input is needed to allow the reaction to take place. Instead, excess energy is generated and liberated when such reactions take place. In the former (endothermic) case, the energy needed by the reaction usually comes from the kinetic energy of the reacting molecules or molecules that surround them. That is, thermal energy from the environment provides the needed energy. Analogously, for exothermic reactions, the excess energy produced as the reaction proceeds is usually deposited into the kinetic energy of the product molecules and into that of surrounding molecules. For reactions that are very endothermic, it may be virtually impossible for thermal excitation to provide sufficient energy to effect reaction. In such cases, it may be possible to use a light source (i.e., photons whose energy can excite the reactant molecules) to induce reaction. When the light source causes electronic excitation of the reactants (e.g., one might excite one electron in the bound diatomic molecule discussed above from a bonding to an anti-bonding orbital), one speaks of inducing reaction by photochemical means.
Conservation of Orbital Symmetry- the Woodward-Hoffmann Rules
An example of how important it is to understand the changes in bonding that accompany a chemical reaction, let us consider a reaction in which 1,3-butadiene is converted, via ring-closure, to form cyclobutene. Specifically, focus on the four \(\pi\) orbitals of 1,3-butadiene as the molecule undergoes so-called disrotatory closing along which the plane of symmetry which bisects and is perpendicular to the \(C_2-C_3\) bond is preserved. The orbitals of the reactant and product can be labeled as being even-e or odd-o under reflection through this symmetry plane. It is not appropriate to label the orbitals with respect to their symmetry under the plane containing the four C atoms because, although this plane is indeed a symmetry operation for the reactants and products, it does not remain a valid symmetry throughout the reaction path. That is, in applying the Woodward-Hoffmann rules, we symmetry label the orbitals using only those symmetry elements that are preserved throughout the reaction path being examined.
The four \(\pi\) orbitals of 1,3-butadiene are of the following symmetries under the preserved symmetry plane (see the orbitals in Figure 5.5): \(\pi_1= e, \pi_2= o, \pi_3=e, \pi_4= o\). The \(\pi\) and \(\pi^*\) and \(\sigma\) and \(\sigma^*\) orbitals of the product cyclobutane, which evolve from the four orbitals of the 1,3-butadiene, are of the following symmetry and energy order: \(\sigma = e, \pi = e, \pi^* = o, \sigma^* = o\). The Woodward-Hoffmann rules instruct us to arrange the reactant and product orbitals in order of increasing energy and to then connect these orbitals by symmetry, starting with the lowest energy orbital and going through the highest energy orbital. This process gives the following so-called orbital correlation diagram:
We then need to consider how the electronic configurations in which the electrons are arranged as in the ground state of the reactants evolves as the reaction occurs.
We notice that the lowest two orbitals of the reactants, which are those occupied by the four \(\pi\) electrons of the reactant, do not connect to the lowest two orbitals of the products, which are the orbitals occupied by the two \(\sigma\) and two \(\pi\) electrons of the products. This causes the ground-state configuration of the reactants (\(\pi_1{}^2 \pi_2{}^2\)) to evolve into an excited configuration (\(\sigma^2 \pi^{*2}\)) of the products. This, in turn, produces an activation barrier for the thermal disrotatory rearrangement (in which the four active electrons occupy these lowest two orbitals) of 1,3-butadiene to produce cyclobutene.
If the reactants could be prepared, for example by photolysis, in an excited state having orbital occupancy \(\pi_1{}^2\pi_2{}^1\pi_3{}^1\), then reaction along the path considered would not have any symmetry-imposed barrier because this singly excited configuration correlates to a singly-excited configuration \(\sigma^2\pi^1\pi^{*1}\) of the products. The fact that the reactant and product configurations are of equivalent excitation level causes there to be no symmetry constraints on the photochemically induced reaction of 1,3-butadiene to produce cyclobutene. In contrast, the thermal reaction considered first above has a symmetry-imposed barrier because the orbital occupancy is forced to rearrange (by the occupancy of two electrons from \(\pi_2{}^2 = \pi^{*2}\) to \(\pi^2 = \pi_3{}^2\)) for the ground-state wave function of the reactant to smoothly evolve into that of the product. Of course, if the reactants could be generated in an excited state having \(\pi_1{}^2 \pi_3{}^2\) orbital occupancy, then products could also be produced directly in their ground electronic state. However, it is difficult, if not impossible, to generate such doubly-excited electronic states, so it is rare that one encounters reactions being induced via such states.
It should be stressed that although these symmetry considerations may allow one to anticipate barriers on reaction potential energy surfaces, they have nothing to do with the thermodynamic energy differences of such reactions. What the above Woodward-Hoffmann symmetry treatment addresses is whether there will be symmetry-imposed barriers above and beyond any thermodynamic energy differences. The enthalpies of formation of reactants and products contain the information about the reaction's overall energy balance and need to be considered independently of the kind of orbital symmetry analysis just introduced.
As the above example illustrates, whether a chemical reaction occurs on the ground or an excited-state electronic surface is important to be aware of. This example shows that one might want to photo-excite the reactant molecules to cause the reaction to occur at an accelerated rate. With the electrons occupying the lowest-energy orbitals, the ring closure reaction can still occur, but it has to surmount a barrier to do so (it can employ thermal collision al energy to surmount this barrier), so its rate might be slow. If an electron is excited, there is no symmetry barrier to surmount, so the rate can be greater. Reactions that take place on excited states also have a chance to produce products in excited electronic states, and such excited-state products may emit light. Such reactions are called chemiluminescent because they produce light (luminescence) by way of a chemical reaction.
Rates of change
Rates of reactions play crucial roles in many aspects of our lives. Rates of various biological reactions determine how fast we metabolize food, and rates at which fuels burn in air determine whether an explosion or a calm flame will result. Chemists view the rate of any reaction among molecules (and perhaps photons or electrons if they are used to induce excitation in reactant molecules) to be related to (1) the frequency with which the reacting species encounter one another and (2) the probability that a set of such species will react once they do encounter one another. The former aspects relate primarily to the concentrations of the reacting species and the speeds with which they are moving. The latter have more to do with whether the encountering species collide in a favorable orientation (e.g., do the enzyme and substrate dock properly, or does the \(Br^-\) ion collide with the \(H_3C^-\) end of \(H_3C-Cl\) or with the \(Cl\) end in the SN2 reaction that yields \(CH_3Br + Cl^-\) ?) and with sufficient energy to surmount any barrier that must be passed to effect breaking bonds in reactants to form new bonds in products.
The rates of reactions can be altered by changing the concentrations of the reacting species, by changing the temperature, or by adding a catalyst. Concentrations and temperature control the collision rates among molecules, and temperature also controls the energy available to surmount barriers. Catalysts are molecules that are not consumed during the reaction but which cause the rate of the reaction to be increased (species that slow the rate of a reaction are called inhibitors). Most catalysts act by providing orbitals of their own that interact with the reacting molecules’ orbitals to cause the energies of the latter to be lowered as the reaction proceeds. In the ring-closure reaction cited earlier, the catalyst’s orbitals would interact (i.e., overlap) with the 1,3-butadiene’s \(\pi\) orbitals in a manner that lowers their energies and thus reduces the energy barrier that must be overcome for reaction to proceed
In addition to being capable of determining the geometries (bond lengths and angles), energies, vibrational frequencies of species such as the isomers of arginine discussed above, theory also addresses questions of how and how fast transitions among these isomers occur. The issue of how chemical reactions occur focuses on the mechanism of the reaction, meaning how the nuclei move and how the electronic orbital occupancies change as the system evolves from reactants to products. In a sense, understanding the mechanism of a reaction in detail amounts to having a mental moving picture of how the atoms and electrons move as the reaction is occurring.
The issue of how fast reactions occur relates to the rates of chemical reactions. In most cases, reaction rates are determined by the frequency with which the reacting molecules access a critical geometry (called the transition state or activated complex) near which bond breaking and bond forming takes place. The reacting molecules’ potential energy along the path connecting reactants through a transition state to produces is often represented as shown in Figure 5.7.
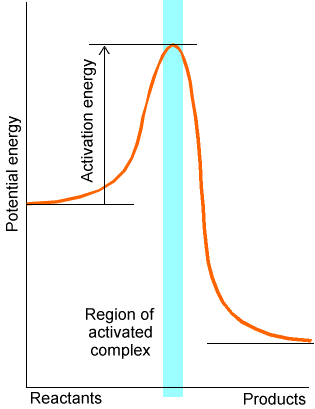
Figure 5.7 Energy vs. reaction progress plot showing the transition state or activated complex and the activation energy.
In this figure, the potential energy (i.e., the electronic energy without the nuclei’s kinetic energy included) is plotted along a coordinate connecting reactants to products. The geometries and energies of the reactants, products, and of the activated complex can be determined using the potential energy surface searching methods discussed briefly above and detailed earlier in Chapter 3. Chapter 8 provides more information about the theory of reaction rates and how such rates depend upon geometrical, energetic, and vibrational properties of the reacting molecules.
The frequencies with which the transition state is accessed are determined by the amount of energy (termed the activation energy \(E^*\)) needed to access this critical geometry. For systems at or near thermal equilibrium, the probability of the molecule gaining energy \(E^*\) is shown for three temperatures in Figure 5.8.
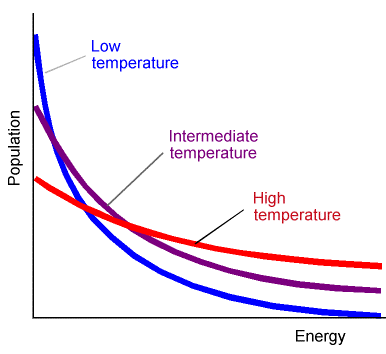
For such cases, chemical reaction rates usually display a temperature dependence characterized by linear plots of \(\ln(k)\) vs \(1/T\). Of course, not all reactions involve molecules that have been prepared at or near thermal equilibrium. For example, in supersonic molecular beam experiments, the kinetic energy distribution of the colliding molecules is more likely to be of the type shown in Figure 5.9.
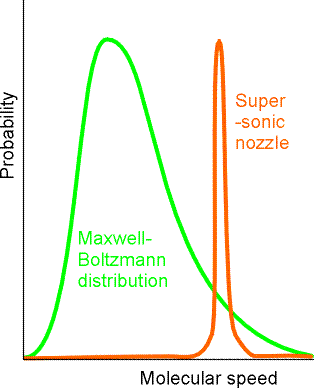
In this figure, the probability is plotted as a function of the relative speed with which reactant molecules collide. It is common in making such collision speed plots to include the \(v^2\) volume element factor in the plot. That is, the normalized probability distribution for molecules having reduced mass m to collide with relative velocity components \(v_z, v_y, v_z\) is
\[P(v_x, v_y, v_z) dv_x dv_y dv_z = \bigg(\dfrac{\mu}{2\pi kT}\bigg)^{3/2} \exp\bigg(-\dfrac{\mu(v_x^2+v_y^2+v_z^2)}{2kT}\bigg) dv_x dv_y dv_z.\]
Because only the total collisional kinetic energy is important in surmounting reaction barriers, we convert this Cartesian velocity component distribution to one in terms of \(v = \sqrt{v_x^2+v_y^2+v_z^2}\) the collision speed. This is done by changing from Cartesian to polar coordinates (in which the radial variable is v itself) and gives (after integrating over the two angular coordinates):
\[P(v) dv = 4p \bigg(\dfrac{\mu}{2\pi kT}\bigg)^{3/2} \exp\bigg(-\dfrac{\mu v^2}{2kT}\bigg) v^2 dv.\]
It is the \(v^2\) factor in this speed distribution that causes the Maxwell-Boltzmann distribution to vanish at low speeds in the above plot.
Another kind of experiment in which non-thermal conditions are used to extract information about activation energies occurs within the realm of ion-molecule reactions where one uses collision-induced dissociation (CID) to break a molecule apart. For example, when a complex consisting of a \(Na^+\) cation bound to a uracil molecule is accelerated by an external electric field to a kinetic energy \(E\) and subsequently allowed to impact into a gaseous sample of Xe atoms, the high-energy collision allows kinetic energy to be converted into internal energy. This collisional energy transfer may deposit into the Na+(uracil) complex enough energy to fragment the \(Na^+\) …uracil attractive binding energy, thus producing \(Na^+\) and neutral uracil fragments. If the signal for production of \(Na^+\) is monitored as the collision energy \(E\) is increased, one generates a CID reaction rate profile such as I show in Figure 5.10.
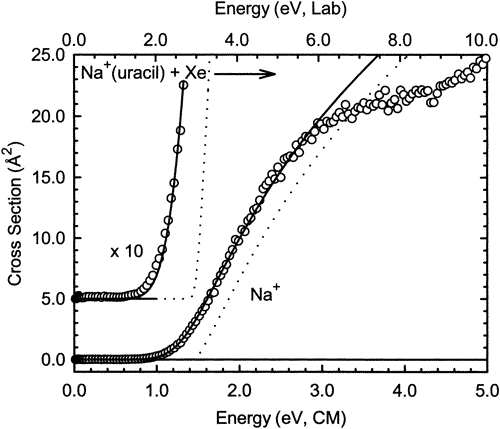
On the vertical axis is plotted a quantity proportional to the rate at which \(Na^+\) ions are formed. On the horizontal axis is plotted the collision energy \(E\) in two formats. The laboratory kinetic energy is simply 1/2 the mass of the \(Na^+({\rm uracil})\) complex multiplied by the square of the speed of these ion complexes measured with respect to a laboratory-fixed coordinate frame. The center-of-mass (CM) kinetic energy is the amount of energy available between the \(Na^+({\rm uracil})\) complex and the Xe atom, and is given by
\[E_{\rm CM} = \dfrac{1}{2} \dfrac{m_{\rm complex} m_{Xe}}{m_{\rm complex} + m_{Xe}} v^2,\]
where \(v\) is the relative speed of the complex and the Xe atom, and \(m_{Xe}\) and \(m_{\rm complex}\) are the respective masses of the colliding partners.
The most essential lesson to learn from such a graph is that no dissociation occurs if \(E\) is below some critical threshold value, and the CID reaction
\[Na^+({\rm uracil}) \rightarrow Na^+ + {\rm uracil}\]
occurs with higher and higher rate as the collision energy \(E\) increases beyond the threshold. For the example shown above, the threshold energy is ca. 1.2-1.4 eV. These CID thresholds can provide us with estimates of reaction endothermicities and are especially useful when these energies are greatly in excess of what can be realized by simply heating the sample.
Statistical Mechanics: Treating Large Numbers of Molecules in Close Contact
When one has a large number of molecules that undergo frequent collisions (thereby exchanging energy, momentum, and angular momentum), the behavior of this collection of molecules can often be described in a simple way. At first glance, it seems unlikely that the treatment of a large number of molecules could require far less effort than that required to describe one or a few such molecules.
To see the essence of what I am suggesting, consider a sample of 10 cm3 of water at room temperature and atmospheric pressure. In this macroscopic sample, there are approximately 3.3 x1023 water molecules. If one imagines having an instrument that could monitor the instantaneous speed of a selected molecule, one would expect the instrumental signal to display a very jerky irregular behavior if the signal were monitored on time scales of the order of the time between molecular collisions. On this time scale, the water molecule being monitored may be moving slowly at one instant, but, upon collision with a neighbor, may soon be moving very rapidly. In contrast, if one monitors the speed of this single water molecule over a very long time scale (i.e., much longer than the average time between collisions), one obtains an average square of the speed that is related to the temperature \(T\) of the sample via \(\dfrac{1}{2} mv^2 = \dfrac{3}{2} kT\). This relationship holds because the sample is at equilibrium at temperature \(T\).
An example of the kind of behavior I describe above is shown in Figure 5.11.
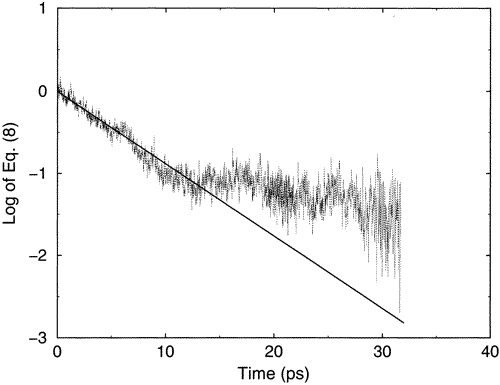
In this figure, on the vertical axis is plotted the log of the energy (kinetic plus potential) of a single \(CN^-\) anion in a solution with water as the solvent as a function of time. The vertical axis label says Eq.(8) because this figure was taken from a literature article. The \(CN^-\) ion initially has excess vibrational energy in this simulation which was carried out in part to model the energy flow from this hot solute ion to the surrounding solvent molecules. One clearly sees the rapid jerks in energy that this ion experiences as it undergoes collisions with neighboring water molecules. These jerks occur approximately every 0.01 ps, and some of them correspond to collisions that take energy from the ion and others to collisions that given energy to the ion. On longer time scales (e.g., over 1-10 ps), we also see a gradual drop off in the energy content of the \(CN^-\) ion which illustrates the slow loss of its excess energy on the longer time scale.
Now, let’s consider what happens if we monitor a large number of molecules rather than a single molecule within the 1 cm3 sample of \(H_2O\) mentioned earlier. If we imagine drawing a sphere of radius \(R\) and monitoring the average speed of all water molecules within this sphere, we obtain a qualitatively different picture if the sphere is large enough to contain many water molecules. For large R, one finds that the average square of the speed of all the \(N\) water molecules residing inside the sphere (i.e., \(\displaystyle\sum_{K =1}^N \dfrac{1}{2} mv_K^2\)) is independent of time (even when considered at a sequence of times separated by fractions of ps) and is related to the temperature \(T\) through \(\displaystyle\sum_K \dfrac{1}{2} mv_K^2 = \dfrac{3N}{2} kT\).
This example shows that, at equilibrium, the long-time average of a property of any single molecule is the same as the instantaneous average of this same property over a large number of molecules. For the single molecule, one achieves the average value of the property by averaging its behavior over time scales lasting for many, many collisions. For the collection of many molecules, the same average value is achieved (at any instant of time) because the number of molecules within the sphere (which is proportional to \(\dfrac{4}{3} \pi R^3\)) is so much larger than the number near the surface of the sphere (proportional to \(4\pi R^2\)) that the molecules interior to the sphere are essentially at equilibrium for all times.
Another way to say the same thing is to note that the fluctuations in the energy content of a single molecule are very large (i.e., the molecule undergoes frequent large jerks) but last a short time (i.e., the time between collisions). In contrast, for a collection of many molecules, the fluctuations in the energy for the whole collection are small at all times because fluctuations take place by exchange of energy with the molecules that are not inside the sphere (and thus relate to the surface area to volume ratio of the sphere).
So, if one has a large number of molecules that one has reason to believe are at thermal equilibrium, one can avoid trying to follow the instantaneous short-time detailed dynamics of any one molecule or of all the molecules. Instead, one can focus on the average properties of the entire collection of molecules. What this means for a person interested in theoretical simulations of such condensed-media problems is that there is no need to carry out a Newtonian molecular dynamics simulation of the system (or a quantum simulation) if it is at equilibrium because the long-time averages of whatever is calculated can be found another way. How one achieves this is through the magic of statistical mechanics and statistical thermodynamics. One of the most powerful of the devices of statistical mechanics is the so-called Monte-Carlo simulation algorithm. Such theoretical tools provide a direct way to compute equilibrium averages (and small fluctuations about such averages) for systems containing large numbers of molecules. In Chapter 7, I provide a brief introduction to the basics of this sub-discipline of theoretical chemistry where you will learn more about this exciting field.
Sometimes we speak of the equilibrium behavior or the dynamical behavior of a collection of molecules. Let me elaborate a little on what these phrases mean. Equilibrium properties of molecular collections include the radial and angular distribution functions among various atomic centers. For example, the O-O and \(O-H\) radial distribution functions in liquid water and in ice are shown in Figure 5.12.
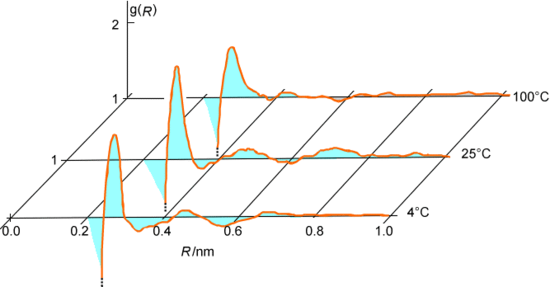
Such properties represent averages, over long times or over a large collection of molecules, of some property that is not changing with time except on a very fast time scale corresponding to individual collisions.
In contrast, dynamical properties of molecular collections include the folding and unfolding processes that proteins and other polymers undergo; the migrations of protons from water molecule to water molecule in liquid water and along \(H_2O\) chains within ion channels; and the self assembly of molecular monolayers on solid surfaces as the concentration of the molecules in the liquid overlayer varies. These are properties that occur on time scales much longer than those between molecular collisions and on time scales that we wish to probe by some experiment or by simulation.
Having briefly introduced the primary areas of theoretical chemistry- structure, dynamics, and statistical mechanics, let us now examine each of them in somewhat greater detail, keeping in mind that Chapters 6-8 are where each is treated more fully.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


