2.8: Rotations of Molecules
- Page ID
- 17182
Rotational Motion For Rigid Diatomic and Linear Polyatomic Molecules
This Schrödinger equation relates to the rotation of diatomic and linear polyatomic molecules. It also arises when treating the angular motions of electrons in any spherically symmetric potential.
A diatomic molecule with fixed bond length \(R\) rotating in the absence of any external potential is described by the following Schrödinger equation:
\[- \frac{\hbar^2}{2\mu} \left[
\frac{1}{R^2\sin\theta}\frac{\partial}{\partial \theta} \left(\sin\theta \frac{\partial}{\partial \theta} \right)
+
\frac{1}{R^2\sin^2\theta} \frac{\partial^2}{\partial \phi^2}
\right] \psi = E \psi\]
or
\[\frac{\textbf{L}^2\psi}{2\mu R^2} = E \psi,\]
where \(\textbf{L}^2\) is the square of the total angular momentum operator \(\textbf{L}_x^2 + \textbf{L}_y^2 + \textbf{L}_z^2\) expressed in polar coordinates above. The angles \(\theta\) and \(\phi\) describe the orientation of the diatomic molecule's axis relative to a laboratory-fixed coordinate system, and \(\mu\) is the reduced mass of the diatomic molecule \(\mu=\dfrac{m_1m_2}{m_1+m_2}\). The differential operators can be seen to be exactly the same as those that arose in the hydrogen-like-atom case discussed earlier in this Chapter. Therefore, the same spherical harmonics that served as the angular parts of the wave function in the hydrogen-atom case now serve as the entire wave function for the so-called rigid rotor: \(\psi = Y_{J,M}(\theta,\phi)\). These are exactly the same functions as we plotted earlier when we graphed the \(s (L=0)\), \(p (L=1)\), and \(d (L=2)\) orbitals. The energy eigenvalues corresponding to each such eigenfunction are given as:
\[E_J = \frac{\hbar^2 J(J+1)}{2\mu R^2} = B J(J+1)\]
and are independent of \(M\). Thus each energy level is labeled by \(J\) and is \(2J+1\)-fold degenerate (because \(M\) ranges from \(-J\) to \(J\)). Again, this is just like we saw when we looked at the hydrogen orbitals; the p orbitals are 3-fold degenerate and the d orbitals are 5-fold degenerate. The so-called rotational constant \(B\) (defined as \(\dfrac{\hbar^2}{2\mu R^2}\)) depends on the molecule's bond length and reduced mass. Spacings between successive rotational levels (which are of spectroscopic relevance because, as shown in Chapter 6, angular momentum selection rules often restrict the changes \(\Delta J\) in \(J\) that can occur upon photon absorption to 1,0, and -1) are given by
\[\Delta E = B (J+1)(J+2) - B J(J+1) = 2B(J+1).\]
These energy spacings are of relevance to microwave spectroscopy which probes the rotational energy levels of molecules. In fact, microwave spectroscopy offers the most direct way to determine molecular rotational constants and hence molecular bond lengths.
The rigid rotor provides the most commonly employed approximation to the rotational energies and wave functions of linear molecules. As presented above, the model restricts the bond length to be fixed. Vibrational motion of the molecule gives rise to changes in \(R\), which are then reflected in changes in the rotational energy levels (i.e., there are different \(B\) values for different vibrational levels). The coupling between rotational and vibrational motion gives rise to rotational \(B\) constants that depend on vibrational state as well as dynamical couplings, called centrifugal distortions, which cause the total ro-vibrational energy of the molecule to depend on rotational and vibrational quantum numbers in a non-separable manner.
Within this rigid rotor model, the absorption spectrum of a rigid diatomic molecule should display a series of peaks, each of which corresponds to a specific \(J \rightarrow J+1\) transition. The energies at which these peaks occur should grow linearly with \(J\) as shown above. An example of such a progression of rotational lines is shown in the Figure 2.23.
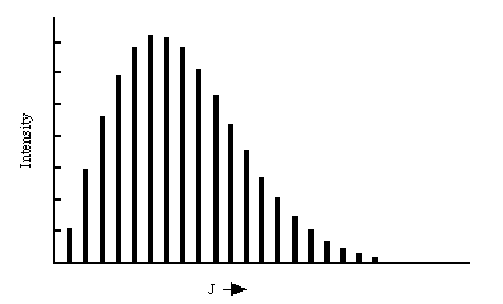
The energies at which the rotational transitions occur appear to fit the \(\Delta E = 2B (J+1)\) formula rather well. The intensities of transitions from level \(J\) to level \(J+1\) vary strongly with \(J\) primarily because the population of molecules in the absorbing level varies with \(J\). These populations \(P_J\) are given, when the system is at equilibrium at temperature \(T\), in terms of the degeneracy (\(2J+1\)) of the Jth level and the energy of this level \(B J(J+1)\) by the Boltzmann formula:
\[P_J = \frac{1}{Q} (2J+1) \exp\bigg(-\dfrac{BJ(J+1)}{kT}\bigg),\]
where \(Q\) is the rotational partition function:
\[Q = \sum_J (2J+1) \exp\bigg(-\dfrac{BJ(J+1)}{kT}\bigg).\]
For low values of \(J\), the degeneracy is low and the \(\exp(-BJ(J+1)/kT)\) factor is near unity. As \(J\) increases, the degeneracy grows linearly but the \(\exp(-BJ(J+1)/kT)\) factor decreases more rapidly. As a result, there is a value of \(J\), given by taking the derivative of \((2J+1) \exp(-BJ(J+1)/kT)\) with respect to \(J\) and setting it equal to zero,
\[2J_{\rm max}+ 1 =\sqrt{\frac{2kT}{B}}\]
at which the intensity of the rotational transition is expected to reach its maximum. This behavior is clearly displayed in the above figure.
The eigenfunctions belonging to these energy levels are the spherical harmonics \(Y_{L,M}(\theta,\phi)\) which are normalized according to
\[\int_0^\pi\int_0^{2\pi}Y_{L,M}^*(\theta,\phi)Y_{L',M'}(\theta,\phi)\sin\theta d\theta d\phi= \delta_{L,L'} \delta_{m,m^\prime} .\]
As noted above, these functions are identical to those that appear in the solution of the angular part of Hydrogenic atoms. The above energy levels and eigenfunctions also apply to the rotation of rigid linear polyatomic molecules; the only difference is that the moment of inertia I entering into the rotational energy expression, which is \(\mu R^2\) for a diatomic, is given by
\[I = \sum_a m_a R_a^2\]
where ma is the mass of the \(a^{\rm th}\) atom and \(R_a\) is its distance from the center of mass of the molecule to this atom.
Rotational Motions of Rigid Non-Linear Molecules
The Rotational Kinetic Energy
The classical rotational kinetic energy for a rigid polyatomic molecule is
\[H_{\rm rot} = \frac{J_a^2}{2I_a} + \frac{J_b^2}{2I_b} + \frac{J_c^2}{2I_c}\]
where the \(I_k (k = a, b, c)\) are the three principal moments of inertia of the molecule (the eigenvalues of the moment of inertia tensor). This tensor has elements in a Cartesian coordinate system (\(K, K' = X, Y, Z\)), whose origin is located at the center of mass of the molecule, that can be computed as:
\[I_{K,K} = \sum_j m_j (R_j^2 - R_{K,j}^2) \hspace{1cm} (\text{for }K = K')\]
\[I_{K,K'} = - \sum_j m_j R_{K,j} R_{K',j} \hspace{1cm} (\text{for } K \ne K').\]
As discussed in more detail in R. N. Zare, Angular Momentum, John Wiley, New York (1988), the components of the corresponding quantum mechanical angular momentum operators along the three principal axes are:
\[\textbf{J}_a = -i\hbar \cos\chi \left[\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi} \right] -i\hbar \sin\chi \frac{\partial}{\partial \theta}\]
\[\textbf{J}_b = i\hbar \sin\chi \left[\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi}\right] -i\hbar \cos\chi \frac{\partial}{\partial \theta}\]
\[\textbf{J}_c = - i\hbar \frac{\partial}{\partial \chi} .\]
The angles \(\theta\), \(\phi\), and \(\chi\) are the Euler angles needed to specify the orientation of the rigid molecule relative to a laboratory-fixed coordinate system. The corresponding square of the total angular momentum operator \(\textbf{J}^2\) can be obtained as
\[\textbf{J}^2 = \textbf{J}_a^2 + \textbf{J}_b^2 + \textbf{J}_c^2\]
\[= - \hbar^2 \frac{\partial^2}{\partial \theta^2} - \hbar^2\cot\theta \frac{\partial}{\partial \theta} + \hbar^2 \frac{1}{\sin^2\theta} \left[\frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \chi^2} - 2 \cos\theta\frac{\partial^2}{\partial \phi\partial \chi} \right],\]
and the component along the lab - fixed \(Z\) axis \(J_Z\) is \(- i\hbar \partial /\partial \phi\) as we saw much earlier in this text.
The Eigenfunctions and Eigenvalues for Special Cases
Spherical Tops
When the three principal moment of inertia values are identical, the molecule is termed a spherical top. In this case, the total rotational energy can be expressed in terms of the total angular momentum operator \(\textbf{J}^2 \)
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I}.\]
As a result, the eigenfunctions of \(\textbf{H}_{\rm rot}\) are those of \(\textbf{J}^2\) and \(J_a\) as well as \(J_Z\) both of which commute with \(\textbf{J}^2\) and with one another. \(J_Z\) is the component of \(J\) along the lab-fixed \(Z\)-axis and commutes with \(J_a\) because \(J_Z = - i\hbar \partial /\partial \phi\) and \(J_a = - i\hbar \partial /\partial \chi\) act on different angles. The energies associated with such eigenfunctions are
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2},\]
for all \(K\) (i.e., \(J_a\) quantum numbers) ranging from \(-J\) to \(J\) in unit steps and for all \(M\) (i.e., \(J_Z\) quantum numbers) ranging from \(-J\) to \(J\). Each energy level is therefore \((2J + 1)^2\) degenerate because there are \(2J + 1\) possible \(K\) values and \(2J + 1\) possible \(M\) values for each \(J\).
The eigenfunctions \(|J,M,K\rangle \) of \(\textbf{J}^2\), \(J_Z\) and \(J_a\) , are given in terms of the set of so-called rotation matrices \(D_{J,M,K}\):
\[|J,M,K\rangle = \sqrt{\frac{2J+1}{8\pi^2}}D^*_{J,M,K}(\theta,\phi,\chi)\]
which obey
\[\textbf{J}^2|J,M,K\rangle = \hbar^2 J(J+1) |J,M,K\rangle ,\]
\[\textbf{J}_a |J,M,K\rangle = \hbar K |J,M,K\rangle ,\]
\[\textbf{J}_Z |J,M,K\rangle = \hbar M |J,M,K\rangle .\]
These \(D_{J,M,K}\) functions are proportional to the spherical harmonics \(Y_{J,M}(\theta,\phi)\) multiplied by \(\exp(iK\chi)\), which reflects its c-dependence.
Symmetric Tops
Molecules for which two of the three principal moments of inertia are equal are called symmetric tops. Those for which the unique moment of inertia is smaller than the other two are termed prolate symmetric tops; if the unique moment of inertia is larger than the others, the molecule is an oblate symmetric top. An American football is prolate, and a Frisbee is oblate.
Again, the rotational kinetic energy, which is the full rotational Hamiltonian, can be written in terms of the total rotational angular momentum operator \(\textbf{J}^2\) and the component of angular momentum along the axis with the unique principal moment of inertia:
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_a^2\left[\frac{1}{2I_a} - \frac{1}{2I}\right]\text{, for prolate tops}\]
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_c^2\left[\frac{1}{2I_c} - \frac{1}{2I}\right]\text{, for oblate tops}\]
Here, the moment of inertia I denotes that moment that is common to two directions; that is, I is the non-unique moment of inertia. As a result, the eigenfunctions of \(H_{\rm rot}\) are those of \(\textbf{J}^2\) and \(J_a\) or \(J_c\) (and of \(J_Z\)), and the corresponding energy levels are:
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_a} - \frac{1}{2I}\right],\]
for prolate tops
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_c} - \frac{1}{2I}\right],\]
for oblate tops, again for \(K\) and \(M\) (i.e., \(J_a\) or \(J_c\) and \(J_Z\) quantum numbers, respectively) ranging from \(-J\) to \(J\) in unit steps. Since the energy now depends on \(K\), these levels are only \(2J + 1\) degenerate due to the \(2J + 1\) different \(M\) values that arise for each \(J\) value. Notice that for prolate tops, because \(I_a\) is smaller than \(I\), the energies increase with increasing \(K\) for given \(J\). In contrast, for oblate tops, since \(I_c\) is larger than \(I\), the energies decrease with \(K\) for given \(J\). The eigenfunctions \(|J, M,K\rangle \) are the same rotation matrix functions as arise for the spherical-top case, so they do not require any further discussion at this time.
iii. Asymmetric Tops
The rotational eigenfunctions and energy levels of a molecule for which all three principal moments of inertia are distinct (a so-called asymmetric top) cannot analytically be expressed in terms of the angular momentum eigenstates and the \(J, M,\) and \(K\) quantum numbers. In fact, no one has ever solved the corresponding Schrödinger equation for this case. However, given the three principal moments of inertia \(I_a\), \(I_b\), and \(I_c\), a matrix representation of each of the three contributions to the rotational Hamiltonian
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}_a^2}{2I_a} + \frac{\textbf{J}_b^2}{2I_b} + \frac{\textbf{J}_c^2}{2I_c}\]
can be formed within a basis set of the {\(|J, M, K\rangle \)} rotation-matrix functions discussed earlier. This matrix will not be diagonal because the \(|J, M, K\rangle \) functions are not eigenfunctions of the asymmetric top \(\textbf{H}_{\rm rot}\). However, the matrix can be formed in this basis and subsequently brought to diagonal form by finding its eigenvectors {\(C_{n, J,M,K}\)} and its eigenvalues {\(E_n\)}. The vector coefficients express the asymmetric top eigenstates as
\[\psi_n (\theta,\phi,\chi) = \sum_{J, M, K} C_{n, J,M,K} |J, M, K\rangle .\]
Because the total angular momentum \(\textbf{J}^2\) still commutes with \(H_{\rm rot}\), each such eigenstate will contain only one \(\textbf{J}_{-}\) value, and hence \(\psi_n\) can also be labeled by a \(J\) quantum number:
\[\psi_{n,J} (\theta,\phi,\chi) = \sum_{M, K} C_{n, J,M,K} |J, M, K\rangle .\]
To form the only non-zero matrix elements of \(H_{\rm rot}\) within the \(|J, M, K\rangle \) basis, one can use the following properties of the rotation-matrix functions (see, for example, R. N. Zare, Angular Momentum, John Wiley, New York (1988)):
\[\langle J, M, K| \textbf{J}_a^2| J, M, K\rangle = \langle J, M, K| \textbf{J}_b^2| J, M, K\rangle \]
\[= \frac{1}{2} \langle J, M, K| \textbf{J}^2 - \textbf{J}_c^2 | J, M, K\rangle = \hbar^2 [ J(J+1) - K^2 ],\]
\[\langle J, M, K| \textbf{J}_c^2| J, M, K\rangle = \hbar^2 K^2,\]
\[\langle J, M, K| \textbf{J}_a^2| J, M, K ± 2\rangle = - \langle J, M, K| \textbf{J}_b^2| J, M, K ± 2\rangle \]
\[= \hbar^2 \sqrt{J(J+1) - K(K± 1)} \sqrt{J(J+1) -(K± 1)(K± 2)}\]
\[\langle J, M, K| \textbf{J}_c^2| J, M, K ± 2\rangle = 0.\]
Each of the elements of \(\textbf{J}_c^2\), \(\textbf{J}_a^2\), and \(\textbf{J}_b^2\) must, of course, be multiplied, respectively, by \(\dfrac{1}{2I_c}\), \(\dfrac{1}{2I_a}\), and \(\dfrac{1}{2I_b}\) and summed together to form the matrix representation of \(H_{\rm rot}\). The diagonalization of this matrix then provides the asymmetric top energies and wave functions.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)