7.7: Derivation of the Van der Waals equation
- Page ID
- 5246
As a specific example of the application of perturbation theory, we consider the Van der Waals equation of state. Let \(U_0\) be given by a pair potential:
\[ U_0({{\textbf r}_1,...,{\textbf r}_N}) = {1 \over 2}\sum_{i\neq j} u_0(\vert{\textbf r}_i-{\textbf r}_j\vert) \nonumber \]
with
\[u_0(r) = \left\{\matrix{0 & \;\;\;\;\;\;\;\;r>\sigma \cr\infty & \;\;\;\;\;\;\;\;\;\;r\leq \sigma}\right. \nonumber \]
This potential is known as the hard sphere potential. In the low-density limit, the radial distribution function can be shown to be given correctly by \(g_0(r) \sim \exp(-\beta u_0(r))\) or
\[ \begin{align*} g_0 (r) &= \theta (r - \sigma ) \\[4pt] &= u_1 (r) \end{align*} \]
\(u (r) = u_0 (r) + u_1(r) \) is taken to be some arbitrary attractive potential, whose specific form is not particularly important. Then, the full potential might look like:
\[A^{(1)} \approx u(r)=u_0(r)+u_1(r)\]
Now, the first term in \(A ^{(1)} \) is
\[ \begin{align*} {1 \over 2}\rho^2 V \int _0^{\infty} 4\pi r^2 u_1 (r) g_0 (r) &= {1 \over 2}\rho^2 V\int_0^{\infty}4\pi r^2 u_1(r) \theta (r - \sigma ) \\[4pt] &=2 \pi \rho^2V \int_{\sigma}^{\infty} r^2 u_1(r) dr \equiv -aN \rho \\[4pt] &=a = -2\pi \int_{\sigma}^{\infty} dr r^2 u_1(r) > 0 \end{align*}\]
where \(\sigma\) is a number that depends on \(u_0 (r) \) and the specific form of \(u(r) = u_0 (r) + u_1 (r) \).
Since the potential \( {Z_N (0) } \) is a hard sphere potential, \( {u_0} \) can be determined analytically. If \(u_0 (r) \) were 0, then \( Z_N^{(0)} = V^N \) would describe an ideal gas and
\[Z_N{^{(0)}}= V^N \nonumber\]
However, because two particles may not approach each other closer than a distance \(u_0 (r) \) between their centers, there is some excluded volume:
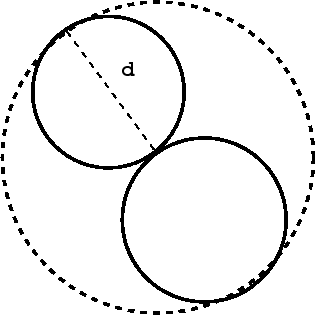
If we consider two hard spheres at closest contact and draw the smallest imaginary sphere that contains both particles, then we find this latter sphere has a radius \(u_0 (r) \):
\[\frac{4}{3} \pi \sigma^3\]
Hence the excluded volume for these two particles is
\[{2 \over 3}\pi \sigma^3 \equiv b \nonumber \]
and hence the excluded volume per particle is just half of this:
\[ Nb \nonumber \]
Therefore \(Z_N{^{(0)}}= (V-Nb)^N\) is the total excluded volume, and we find that, in the low density limit, the partition function is given approximately by
\[A(N,V,T) \approx -{1 \over \beta} \ln \left[{(V-Nb)^N \over N! \lambda^{3N}}\right] - {aN^2 \over V} \nonumber \]
Thus, the free energy is
\[P = -\left({\partial A \over \partial V}\right)_{N,T} \nonumber \]
If we now use this free energy to compute the pressure from
\[{ {P \over kT}} \nonumber \]
we find that
\[ \begin{align*} {N \over V-Nb} - {aN^2 \over kTV^2} &= { {\rho \over 1-\rho b} - {a \rho^2 \over kT} } \\[4pt] &= \rho b \gg 1 \end{align*}\]
This is the well know Van der Waals equation of state. In the very low density limit, we may assume that
\[{1 \over 1-\rho b} \approx 1 + \rho b, \nonumber \]
hence
\[{P \over kT} \approx \rho + \rho^2\left(b-{a \over kT}\right) \nonumber \]
Thus,
\[ B_2 (T) \approx b - {a \over kT} = {2 \over 3} \pi \sigma^3 + {2 \pi \over kT} \int _{\sigma }^{\infty} dr r^2 u_1 (r) \nonumber \]
from which we can approximate the second virial coefficient:
\[B_2(T) \approx b-{a \over kT} = {2 \over 3}\pi \sigma^3 +{2\pi \over kT}\int_{\sigma}^{\infty} dr r^2 u_1(r)\]
A plot of the isotherms of the Van der Waals equation of state is shown below:
\[\frac{\partial P}{\partial V}=0\]
\[\frac{\partial^2 P}{\partial V}=0\]
The red and blue isotherms appear similar to those of an ideal gas, i.e., there is a monotonic decrease of pressure with increasing volume. The black isotherm exhibits an unusual feature not present in any of the ideal-gas isotherms - a small region where the curve is essentially horizontal (flat) with no curvature. At this point, there is no change in pressure as the volume changes. Below this isotherm, the Van der Waals starts to exhibit unphysical behavior. The green isotherm has a region where the pressure decreases with decreasing volume, behavior that is not expected on physical grounds. What is observed experimentally, in fact, is that at a certain pressure, there is a dramatic, discontinuous change in the volume. This dramatic jump in volume signifies that a phase transition has occurred, in this case, a change from a gaseous to a liquid state. The dotted line shows this jump in the volume. Thus, the small flat neighborhood along the black isotherm becomes larger on isotherms below this one. The black isotherm just represents a boundary between those isotherms along which no such phase transition occurs and those that exhibit phase transitions in the form of discontinuous changes in the volume. For this reason, the black isotherm is called the critical isotherm, and the point at which the isotherm is flat and has zero curvature is called a critical point.
A critical point is a point at which
\[V_c \nonumber \]
Using these two conditions, we can solve for the critical volume (\(V_c\)) and critical temperature (\((T_c\)):
\[\begin{align*} V_c &= 3Nb \\[4pt] kT_c &= {8a \over 27b} \\[4pt] P_c &= {a \over 27b^2} \end{align*}\]
and the critical pressure is therefore
\[\kappa_{\rm T} = {1 \over V}{\partial V \over \partial P} \nonumber \]
Using these values for the critical pressure, temperature and volume, we can show that the isothermal compressibility, given by
\[ \left.{\partial P \over \partial V}\right\vert _{V=V_c} =-{NkT \over 2N^2b^2} + {2aN^2 \over 27N^3b^3} = -{kT \over 4Nb^2} + {2a \over 27Nb^3} = {1 \over 4Nb^2}\left({8a \over 27b} - kT\right) \sim (T-T_c) \nonumber \]
diverges as the critical point is approached. To see this, note that
\[\kappa_{T} \sim (T-T_c)^{-1} \nonumber \]
Thus,
\[ {\kappa_T} \nonumber \]
It is observed that at a critical point, \( { \vert T-T_c\vert^{-\gamma}} \) diverges, generally, as \( Q(N,V,T) = e^{-\beta A(N,V,T)} = {(V-Nb)^N \over N!\lambda^{3N}}e^{\beta aN^2/V}\). To determine the heat capacity, note that
\[E \nonumber \]
so that
\( -{\partial \over \partial \beta}\ln Q(N,V,T) = { -{\partial \over \partial \beta}\left[N\ln (V-Nb) - \ln N! - 3N\ln\lambda + {\beta aN^2 \over V}\right]} \)
\(= {{3N \over \lambda}{\partial \lambda \over \partial \beta} + {aN^2 \over V} } \)
\(= {{3N \over \lambda}{\lambda \over \partial \beta} + {aN^2 \over V} } \)
\(= {{3 NkT \over 2} + {aN^2 \over V} } \)
\(= C_V = \left({\partial E \over \partial T}\right)_V\)
Then, since
\[ C_V = {3 \over 2}Nk \sim \vert T-T_c\vert^0 \nonumber \]
it follows that
\[ {\vert T-T_c\vert^{-\alpha} } \nonumber \]
The heat capacity is observed to diverge as \(\alpha \). Exponents such as \( {\gamma} \) and \(\delta \) are known as critial exponents.
Finally, one other exponent we can easily determine is related to how the pressure depends on density near the critical point. The exponent is called \({P \over kT} \sim {\rm const} + C(\rho-\rho_c)^{\delta}\), and it is observed that
\[ {P_c \over kT_c} + {1 \over kT_c}{\partial P \over \partial \rho} \vert _{\rho = \rho _c} (\rho - \rho _c) + {1 \over 2kT_c}{\partial^2 P \over \partial \rho ^2} \vert _{\rho = rho_c} (\rho - \rho _c)^2 + {1 \over 6kT_c}{\partial^3 P \over \partial \rho ^3} \vert _{\rho = \rho_c} (\rho - \rho _c)^3 + \cdots \nonumber \]
What does our theory predict for
\({P \over kT} \sim const + C ( \rho - \rho _c )^{\delta} \)? To determine \({P \over kT} \sim const + C ( \rho - \rho _c )^{\delta} \) we expand the equation of state about the critical density and temperature:
\[ \begin{algin*} {N \over V - Nb} - {aN^2 \over kTV^2} &= {P_c \over kT_c} + {1 \over kT_c}\left.{\partial P \over \partial V}{\partial V \over \partial \rho}_{\rho= \rho_c} (\rho - rho_c) + {1 \over 2kT_c} \left [ {\partial^2 P \over \partial V^2} \left (\partial V \over \partial \rho \right ) + {\partial P \over \partial V}{\partial^2 V \over \partial \rho^2} \right ] \vert_{\rho = \rho_c } (\rho - \rho_c)^2 + {1 \over 6kT_c} {\partial^3 P \over \partial \rho^3}\right\vert _{\rho=\rho_c}(\rho-\rho_c)^3 + \cdots \\[4pt] &= {1 \over kT_c}{\partial ^3 P \over \partial \rho ^3} \vert _{\rho = \rho_c} &= {243 \over 8} b^2 \ne 0 \end{align*}\]
The second and third terms vanish by the conditions of the critical point. The third derivative term can be worked out straightforwardly and does not vanish. Rather
\[ \delta =0 3 \nonumber \]
Thus, we see that, by the above expansion, \(\alpha = 0 \gamma = 1 \delta = 3 \).
The behavior of these quantities near the critical temperature determine three critical exponents. To summarize the results, the Van der Waals theory predicts that
\[ {\alpha = 0.1, \gamma = 1.45} \nonumber \]
The determination of critical exponents such as these is an active area in statistical mechanical research. The reason for this is that such exponents can be grouped into universality classes - groups of systems with exactly the same sets of critical exponents. The existence of universality classes means that very different kinds of systems exhibit essentially the same behavior at a critical point, a fact that makes the characterization of phase transitions via critical exponents quite general. The values obtained above for \( {\gamma} \), \(\delta \) and \( {P \over kT} \sim const + C (\rho - rho_c )^{\delta} \) are known as the mean-field exponents and shows that the Van der Waals theory is really a mean field theory.
These exponents do not agree terribly well with experimental values ( \(\delta = 4.2, {\partial P \over \partial V } > 0 \) ). However, the simplicity of mean-field theory and its ability to give, at least, qualitative results, makes it, nevertheless, useful. To illustrate universality classes, it can be shown that, within mean field theory, the Van der Waals gas/liquid and a magnetic system composed of spins at particular lattice sites, which composes the so called Ising model, have exactly the same mean field theory exponents, despite the completely different nature of these two systems.
Another problem with the Van der Waals theory that is readily apparent is the fact that it predicts \( {\rho } \) for certain values of the density \(g_0 (r) \). Such behavior is unstable. Possible ways of improving the approximations used are the following:
- Improve the approximation to \(U_0 (r_1, \cdots , r_N ) \).
- Choose a better zeroth order potential .
- Go to a higher order in perturbation theory.
Barker and Henderson have shown that going to second order in perturbation theory (see discussion in McQuarrie's book, chapter 14), yields well converged results for a square well fluid, compared to "exact'' results from a molecular dynamics simulation.


