1.4: Phase Space

Last updated
Save as PDF

Page ID: 5100

Mark Tuckerman
New York University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

We construct a Cartesian space in which each of the \(6N\) coordinates and momenta is assigned to one of \(6N\) mutually orthogonal axes. Phase space is, therefore, a \(6N\) dimensional space. A point in this space is specified by giving a particular set of values for the \(6N\) coordinates and momenta. Denote such a point by

\[ x = (p_1, \cdots , p_N, r_1, \cdots , r_N ) \nonumber \]

\(x\) is a \(6N\) dimensional vector. Thus, the time evolution or trajectory of a system as specified by Hamilton's equations of motion, can be expressed by giving the phase space vector, \(x\) as a function of time.

Figure \(\PageIndex{1}\): Evolution of an ensemble of classical systems in phase space (top). The systems are a massive particle in a one-dimensional potential well (red curve, lower figure). The initially compact ensemble becomes swirled up over time.

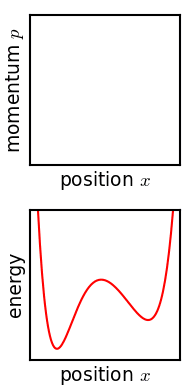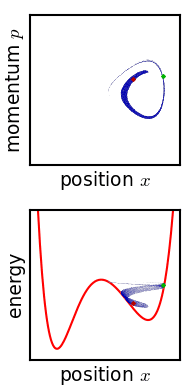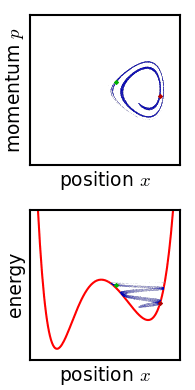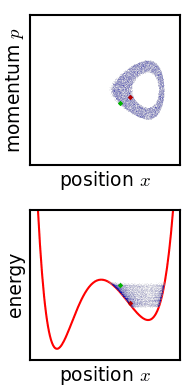
The law of conservation of energy, expressed as a condition on the phase space vector:

\[ H(x(t)) = \text {const} = E \nonumber \]

defines a \(6N - 1\) dimensional hypersurface in phase space on which the trajectory must remain.