Absorption Intensity

Last updated
Save as PDF

Page ID: 1244

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Molar absoptivities may be very large for strongly absorbing chromophores (>10,000) and very small if absorption is weak (10 to 100). The magnitude of \(\epsilon\) reflects both the size of the chromophore and the probability that light of a given wavelength will be absorbed when it strikes the chromophore. A general equation stating this relationship may be written as follows:

\[\epsilon = 0.87 \times 10^{20} \times Ρ \times a\]

with

\(Ρ\) is the transition probability (between 0 to 1) and
\(a\) is the chromophore area in \(cm^^2\)

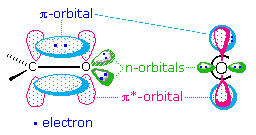
The factors that influence transition probabilities are complex, and are treated by what spectroscopists refer to as "Selection Rules". A rigorous discussion of selection rules is beyond the scope of this text, but one obvious factor is the overlap of the orbitals involved in the electronic excitation. This is nicely illustrated by the two common transitions of an isolated carbonyl group. The \(n \rightarrow \pi^*\) transition is lower in energy (\(\lambda_{max}=290\; nm\)) than the \(\pi \rightarrow \pi^*\) transition (\(\lambda_{max}=180\; nm\)), but the ε of the former is a thousand times smaller than the latter. The spatial distribution of these orbitals suggests why this is so. As illustrated in the following diagram, the n-orbitals do not overlap at all well with the \(\pi*\) orbital, so the probability of this excitation is small. The \(\pi \rightarrow \pi^*\) transition, on the other hand, involves orbitals that have significant overlap, and the probability is near 1.0.

Contributors

William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry