Woodward Hoffmann rules

Robert Burns Woodward and Roald Hoffmann devised these set of rules to explain the stereochemistry of pericyclic reactions based on the orbital symmetry. There are several ways to explain the Woodward Hoffmann rules and are discussed in separate topics. Hoffmann received the 1981 Nobel prize in chemistry along with Fukui (Frontier molecular orbital approach). Woodward had died two years before and therefore was not considered for what could have been his second Nobel prize.

General rule

A general way of stating the Woodward Hoffmann rules for thermal pericyclic reactions:

A ground-state pericyclic change is symmetry-allowed when the total number of (4q + 2)s and (4r)a components is odd.

The subscripts "s" and "a" stand for suprafacial and antarafacial respectively, "q" and "r" stand for integers (0, 1, 2, 3, ...). In the following discussion we will explain how this general rule is applicable in all the pericyclic reactions.

Notes to keep in mind

1. Orbital symmetry is conserved in concerted reactions.
2. In this page, molecular orbitals are symbolized in terms of the atomic orbitals whose interaction give the actual molecular orbital. The relative sizes of the resultant atomic orbital contributions are not identical but are ignored as the nodal properties are the subjects of interest here.
3. It is important to identify the σ and π levels, their corresponding anti-bonding levels while drawing a correlation diagram. The number of levels of each symmetry type on the right hand side of the correlation diagram should match those on the left side.
4. All bonding σ orbitals which are not symmetric or anti-symmetric with respect to every molecular symmetry element must be mixed until they become so.
5. All orbitals of a given symmetry can be mixed with each other for convenience.

Precautions

1. Each basic process must be isolated and analyzed separately. Otherwise the superposition of two forbidden but independent processes may lead one to the erroneous conclusion that the combined process is symmetry-allowed.
2. Only symmetry elements that are present in reactants, products and transition state are useful. Additionally, the symmetry elements chosen for analysis must bisect bonds made or broken in the process. Two corollaries which follow:
   • a symmetry element of no use in analyzing a reaction is one with respect to which the orbitals considered are either all symmetric or all anti-symmetric.
   • if the only symmetry element is one which does not bisect any bonds made or broken, then the correlation diagram constructed based on this element can lead to false conclusion.
3. Each case must be reduced to its highest inherent symmetry. Thus, if there are heteroatoms in a polyene component, they are to be replaced by their isoelectronic carbon groupings. If there are substituents with trivial electronic demands they should be replaced by hydrogens. Heteroatoms can offer new reactivity patterns by the inclusion of the lone pairs or by the availability of low lying unoccupied orbitals. These cases have to be dealt with care.

Side Notes

Robert Burns Woodward was a professor at Harvard University when Roald Hoffmann was a research fellow there. Woodward's lectures often continued for hours. As he was rather slow with chalk drawing, it was easy to take class notes. See the bottom of this page for the videos of his lectures.

• Suprafacial: If a component undergoes addition (forms bond) on the same face, it is called a suprafacial component.
• Antarafacial: If a component undergoes addition on opposite faces, it is called an antarafacial component.
• In a conrotatory mode of an electrocyclic reaction the substituents located at the termini of a conjugated double bond system move in the same (clockwise or counter clockwise) direction during ring opening or ring closure. In a disrotatory mode, they move in opposite directions.
• Correlation diagram: A diagram which shows the relative energies of orbitals, configurations, valence bond structures, or states of reactants and products of a reaction, as a function of the molecular geometry, or another suitable parameter. An example involves the interpolation between the energies obtained for the united atoms and the values for the separated atom limits.
• Conservation of orbital symmetry: IUPAC definition: The orbital symmetry control of concerted reactions; this requires transformation of the molecular orbitals of reactants into those of products to proceed continuously by following a reaction path along which the symmetry of these orbitals remains unchanged. Reactions which adhere to this requirement are classified as symmetry-allowed reactions, and those which do not as symmetry-forbidden reactions.
• Forbidden or allowed? A reaction may be allowed but may also require high energy or in other case, a reaction may be forbidden but may also often occur relatively easily. By the term "forbidden" it is meant that the reaction has a high symmetry imposed barrier along a specific geometry of approach apart from the other factors such as sterics. This does not mean that the reactions cannot happen. Similarly, a reaction may need to overcome high activation energy even though it is symmetry allowed.

Corey's claim on WH rules and Hoffmann's rebuttal: E. J. Corey's claim and Roald Hoffmann's rebuttal are here and you should judge yourself.

Cycloaddition Reactions

Here we will see how Woodward Hoffmann selection rules for cycloaddition are derived. Before doing that let's see how to draw a correlation diagram for a cycloaddition reaction. An example of cycloaddition reaction is the formation of cyclobutane from two ethylene molecules. A simple orbital correlation diagram or orbital symmetry diagram is shown below to explain the outcome of of this reaction. The symmetry element chosen are the mirror planes (plane 1 and plane 2 in section 1.2.)bisecting the bonds made or broken (depicted in blue dotted lines in the correlation diagram, see section 1.3.).

Any other symmetry elements passing through the two ethylene molecules or cyclobutane will not suffice for the discussion of the bond formation of two ethylene molecules (a pictorial description is given below).

Which plane of symmetry to choose

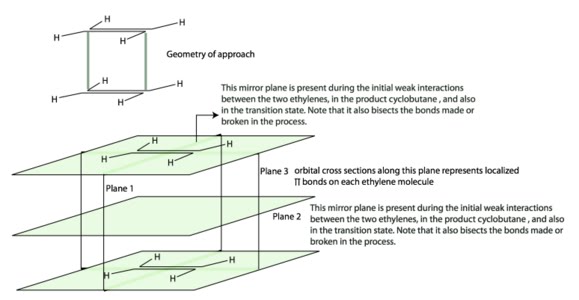
For a simple example, the approach of the two ethylene molecules are considered as parallel. Any other approach is not considered for now. Two mirror planes 1 and 2 are considered as the choice of symmetry elements for the purpose of discussion as they satisfy the required conditions as mentioned in the "precautions" section.

Orbital Correlation Diagram

In the orbital symmetry diagram or the orbital correlation diagram shown in the left, we consider the combinations (π1 + π2) and (π1 - π2) of the two ethylenes and (σ1 + σ2), (σ1 - σ2) of cyclobutane. The energy levels of either of these combinations should be degenerate when the two ethylenes are not interacting or the cyclobutane is not being broken apart. Any weak interactions break the degeneracy of these levels.

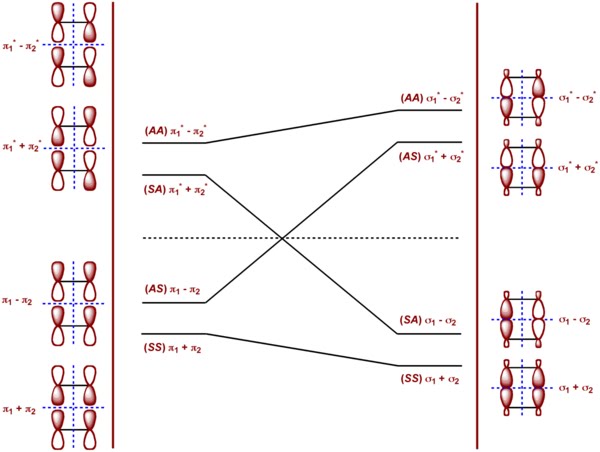
The symmetry labels of the combinations are with respect to the two mirror planes considered here. (SS) represents the orbital symmetry where the π orbitals are symmetric under reflection on both the mirror planes, (AA) represents where they are anti-symmetric, (SA) and (AS) represent levels where the π orbitals are symmetric under one mirror plane but anti-symmetric under the other mirror plane.

Applying the concept of "conservation of orbital symmetry" introduced by Woodward and Hoffmann, it is shown in the diagram how the levels transform along the course of the reaction. The ground state of ethylene becomes a doubly excited state of cyclobutane. The reverse is also true and the ground state of cyclobutane becomes a doubly excited state of ethylene. This is highly undesirable outcome of the reaction and termed as forbidden under thermal conditions.

State Correlation Diagram

For all the pericyclic reactions, orbital correlation diagrams are sufficient to predict the reaction outcome. However, a deeper understanding arises from the corresponding state correlation diagrams. State correlation diagrams deal with the actual quantum mechanical states and not the orbitals. As quantum mechanical states are definite solutions of the Schrödinger equation, they relate directly with the reality. State correlation diagrams can always be used to verify the outcome predicted by the orbital correlation diagram. A simple procedure to assign the state symmetry is shown below.

The figure in the right is showing an example of how to derive the state symmetry based on the individual electron configurations in the orbitals. The symmetry of the states is obtained by multiplying the symmetry labels of each electrons following the rules:

\[S \times S = S = A \times A\]

\[S \times A = A = A \times S\]

(S = symmetric; A = anti-symmetric)

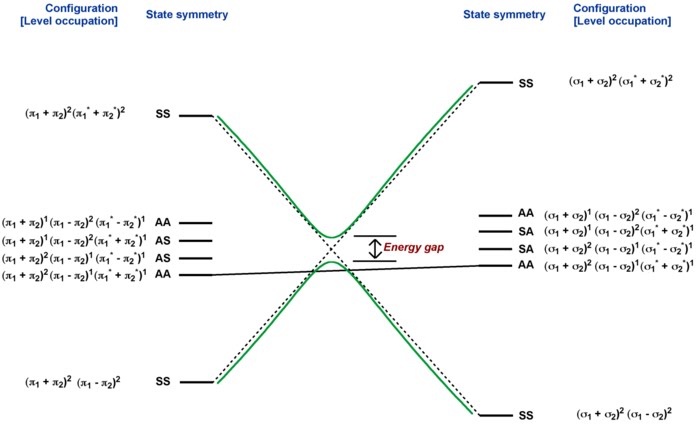
In this diagram, several other excited states are possible which are not relevant for the discussion. The correlated states should have same orbital occupancies in the reactant and the product. The correlated states should also have the same symmetry with respect to each mirror planes.

An important difference between the state correlation and orbital correlation is that in the state correlation states of the same symmetry do not cross. This is known as non-crossing rule. As the energies of the two states with same symmetry approach each other, they mix and diverge. Greater the mixing, higher is the energy gap. Thus the avoided crossing means the ground state of the ethylenes correlates with the ground state of cyclobutane. However, there is a very large symmetry imposed barrier for this reaction and at the first excited state, this barrier is elevated and the reaction becomes symmetry-allowed.

The state correlation diagram corresponds to the reaction co-ordinate and this symmetry imposed barrier could be additional to other energy barriers caused by sterics, etc. Interestingly, the first excited state surface comes very close to the thermal barrier and because of this situation, funnel forms and reaction becomes allowed in the first excited state. However, this does not mean that the photochemical reaction will always follow this concerted pathway. It is often found that an allowed pericyclic photochemical reaction chooses stepwise pathway.

An interesting situation arises when one considers the cycloaddition reaction of two propylene molecules. An extra methyl group on each of ethylene molecule has in an absolute sense reduced the symmetry of all the orbitals to the same level. However, one must restrain from concluding that the reaction has become symmetry allowed. The perturbation due to a mere substitution is very little and the reaction remains symmetry forbidden.

Orthogonal Approach of Two Ethylenes

We have so far seen the parallel approach for [π2s + π2s] cycloaddition is forbidden. What about the orthogonal approach? This can be called [π2s + π2a] reaction. Let us consider the symmetry element involved. Here one of the ethylenes is suprafacial component and the other is the antarafacial component. There is a two fold axis of symmetry (C2) passing through the bonds of two ethylenes perpendicular to the plane of this screen and right through the "green dot" in the figure on the right. This also bisects the bonds to be broken. The orthogonal approach will eventually flatten out and become much flatter cyclobutane. To consider the orthogonal approach we have exaggerated the "twistedness" of cyclobutane.

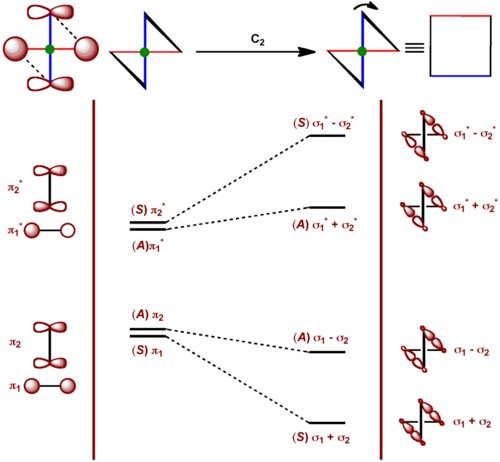
With respect to the C2 axis, the π bonds are well defined i.e., they are either symmetric (S) or anti-symmetric (A). Therefore there s no need to mix them. However, for the σ bonds as they are not independently well defined with respect to C2 axis, we have to mix them as shown in the figure.

We can now see that the ground states of the two ethylenes directly correlate with the ground state of cyclobutane. The reaction is symmetry allowed and if we consider the corresponding state correlation diagram, we will see that there is no symmetry imposed barrier.

The reaction outcome for the first excited state can also be rationalized from the state correlation diagram.

[4 + 2] cycloaddition

A very common example of [4 + 2] cycloaddition would be Diels Alder reaction between cyclobutadiene and ethylene. Here the element of symmetry chosen is the mirror plane bisecting cyclobutadiene and ethylene as shown in the top figure. The orbitals on cyclobutadiene and ethylene are well defined with respect to the plane of symmetry but the σ orbitals on the product cyclohexene are not. In this case, the σ bonds has to be mixed as shown in the left figure.

The orbital correlation diagram clearly shows there is no crossing of levels between bonding and antibonding levels. The ground states of the reactants are correlating with the ground state of cyclohexene. The reaction is symmetry allowed.

Under photochemical conditions, this situation changes. The corresponding state correlation diagram will show that there is large symmetry imposed barrier to make this reaction possible and therefore, the reaction is forbidden in the first excited state.

Selection Rules for Cycloaddition

We just saw that the total number of (4q + 2) suprafacial components and (4r) antarafacial components is even for [π2s + π2s]. Here the (4q + 2) suprafacial components are the two ethylenes and there are no (4r) antarafacial component which implies that the total number is 2 (an even number). According to the general rule, the reaction is forbidden. Using the same rule, [π2s + π2a] cycloaddition should be allowed because we now have one (4q + 2) component and no (4r) component which implies the total number of (4q + 2)s and (4r)a components is 1 (an odd number).

For a two component cycloaddition, the maximum number of modes of addition is 22 = 4 (for n components, it is 2n): (s,s), (s,a), (a,s), (a,a) where s = suprafacial and a = antarafacial.

(m + n)	Thermal	Thermal	Photochemical	Photochemical
	Allowed	Forbidden	Allowed	Forbidden
4q + 2	(s,s) and (a,a)	(s,a) and (a,s)	(s,a) and (a,s)	(s,s) and (a,a)
4q	(s,a) and (a,s)	(s,s) and (a,a)	(s,s) and (a,a)	(s,a) and (a,s)

Electrocyclic Reactions

Woodward Hoffmann general rules for the electrocyclic reactions are as follows:

The thermal electrocyclic reactions of a k π electron system will be disrotatory for k = 4q + 2, conrotatory for k = 4q (q = 0, 1, 2, ...). In the first excited state, these relationships are reversed.

Contributors

• Learning Chemistry