Molecular Shape

The three dimensional shape or configuration of a molecule is an important characteristic. This shape is dependent on the preferred spatial orientation of covalent bonds to atoms having two or more bonding partners. Three dimensional configurations are best viewed with the aid of models. In order to represent such configurations on a two-dimensional surface (paper, blackboard or screen), we often use perspective drawings in which the direction of a bond is specified by the line connecting the bonded atoms.

1. Introduction
2. Isomers
   1. Structural Formulas
   2. Distinguishing Carbon Atoms
3. Analysis of Molecular Formulas
4. Resonance
5. The basic principles of the resonance method may now be summarized.
6. Atomic and Molecular Orbitals
   1. Hybrid Orbitals
7. Molecular Orbitals
8. Contributors

Introduction

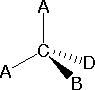
In most cases the focus of configuration is a carbon atom so the lines specifying bond directions will originate there. As defined in the diagram on the right, a simple straight line represents a bond lying approximately in the surface plane. The two bonds to substituents A in the structure on the left are of this kind. A wedge shaped bond is directed in front of this plane (thick end toward the viewer), as shown by the bond to substituent B; and a hatched bond is directed in back of the plane (away from the viewer), as shown by the bond to substituent D. Some texts and other sources may use a dashed bond in the same manner as we have defined the hatched bond, but this can be confusing because the dashed bond is often used to represent a partial bond (i.e. a covalent bond that is partially formed or partially broken).

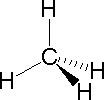
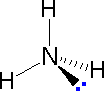
The following examples make use of this notation, and also illustrate the importance of including non-bonding valence shell electron pairs (colored blue) when viewing such configurations.

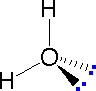Methane	Ammonia	Water

Bonding configurations are readily predicted by valence-shell electron-pair repulsion theory, commonly referred to as VSEPR in most introductory chemistry texts. This simple model is based on the fact that electrons repel each other, and that it is reasonable to expect that the bonds and non-bonding valence electron pairs associated with a given atom will prefer to be as far apart as possible. The bonding configurations of carbon are easy to remember, since there are only three categories.

Configuration	Bonding Partners	Bond Angles	Example
Tetrahedral	4	109.5º
Trigonal	3	120º
Linear	2	180º

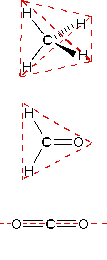
In the three examples shown above, the central atom (carbon) does not have any non-bonding valence electrons; consequently the configuration may be estimated from the number of bonding partners alone. For molecules of water and ammonia, however, the non-bonding electrons must be included in the calculation. In each case there are four regions of electron density associated with the valence shell so that a tetrahedral bond angle is expected. The measured bond angles of these compounds (H₂O 104.5º & NH₃ 107.3º) show that they are closer to being tetrahedral than trigonal or linear. Of course, it is the configuration of atoms (not electrons) that defines the the shape of a molecule, and in this sense ammonia is said to be pyramidal (not tetrahedral). The compound boron trifluoride, BF3, does not have non-bonding valence electrons and the configuration of its atoms is trigonal. Nice treatments of VSEPR theory have been provided by Oxford and Purdue. The best way to study the three-dimensional shapes of molecules is by using molecular models. Many kinds of model kits are available to students and professional chemists.

One way in which the shapes of molecules manifest themselves experimentally is through molecular dipole moments. A molecule which has one or more polar covalent bonds may have a dipole moment as a result of the accumulated bond dipoles. In the case of water, we know that the O-H covalent bond is polar, due to the different electronegativities of hydrogen and oxygen. Since there are two O-H bonds in water, their bond dipoles will interact and may result in a molecular dipole which can be measured. The following diagram shows four possible orientations of the O-H bonds.

The bond dipoles are colored magenta and the resulting molecular dipole is colored blue. In the linear configuration (bond angle 180º) the bond dipoles cancel, and the molecular dipole is zero. For other bond angles (120 to 90º) the molecular dipole would vary in size, being largest for the 90º configuration. In a similar manner the configurations of methane (CH₄) and carbon dioxide (CO₂) may be deduced from their zero molecular dipole moments. Since the bond dipoles have canceled, the configurations of these molecules must be tetrahedral (or square-planar) and linear respectively.

The case of methane provides insight to other arguments that have been used to confirm its tetrahedral configuration. For purposes of discussion we shall consider three other configurations for CH₄, square-planar, square-pyramidal and triangular-pyramidal.

Substitution of one hydrogen by a chlorine atom gives a CH₃Cl compound. Since the tetrahedral, square-planar and square-pyramidal configurations have structurally equivalent hydrogen atoms, they would each give a single substitution product. However, in the trigonal-pyramidal configuration one hydrogen (the apex) is structurally different from the other three (the pyramid base). Substitution in this case should give two different CH₃Cl compounds if all the hydrogens react. In the case of disubstitution, the tetrahedral configuration of methane would lead to a single CH₂Cl₂ product, but the other configurations would give two different CH₂Cl₂ compounds.

Isomers

Structural Formulas

It is necessary to draw structural formulas for organic compounds because in most cases a molecular formula does not uniquely represent a single compound. Different compounds having the same molecular formula are called isomers, and the prevalence of organic isomers reflects the extraordinary versatility of carbon in forming strong bonds to itself and to other elements. When the group of atoms that make up the molecules of different isomers are bonded together in fundamentally different ways, we refer to such compounds as constitutional isomers. There are seven constitutional isomers of C₄H₁₀O, and structural formulas for these are drawn in the following table. These formulas represent all known and possible C₄H₁₀O compounds, and display a common structural feature. There are no double or triple bonds and no rings in any of these structures.

Structural Formulas for C₄H₁₀O isomers

Kekulé Formula	Condensed Formula	Shorthand Formula

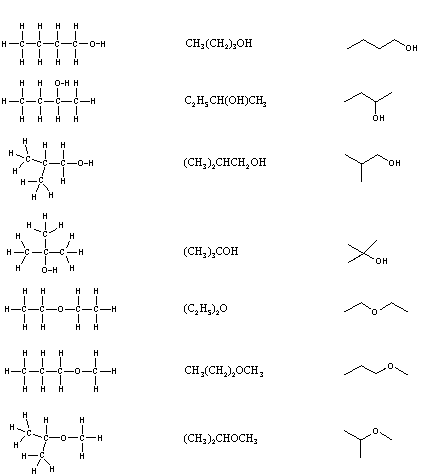Simplification of structural formulas may be achieved without any loss of the information they convey. In condensed structural formulas the bonds to each carbon are omitted, but each distinct structural unit (group) is written with subscript numbers designating multiple substituents, including the hydrogens. Shorthand (line) formulas omit the symbols for carbon and hydrogen entirely. Each straight line segment represents a bond, the ends and intersections of the lines are carbon atoms, and the correct number of hydrogens is calculated from the tetravalency of carbon. Non-bonding valence shell electrons are omitted in these formulas.

Developing the ability to visualize a three-dimensional structure from two-dimensional formulas requires practice, and in most cases the aid of molecular models. As noted earlier, many kinds of model kits are available to students and professional chemists, and the beginning student is encouraged to obtain one.

Constitutional isomers have the same molecular formula, but their physical and chemical properties may be very different. For an example Click Here.

Distinguishing Carbon Atoms

When discussing structural formulas, it is often useful to distinguish different groups of carbon atoms by their structural characteristics. A primary carbon (1º) is one that is bonded to no more than one other carbon atom. A secondary carbon (2º) is bonded to two other carbon atoms, and tertiary (3º) and quaternary (4º) carbon atoms are bonded respectively to three and four other carbons. The three C₅H₁₂ isomers shown below illustrate these terms.

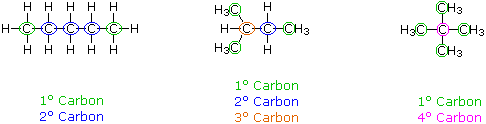
Structural differences may occur within these four groups, depending on the molecular constitution. In the formula on the right all four 1º-carbons are structurally equivalent (remember the tetrahedral configuration of tetravalent carbon); however the central formula has two equivalent 1º-carbons (bonded to the 3º carbon on the left end) and a single, structurally different 1º-carbon (bonded to the 2º-carbon) at the right end. Similarly, the left-most formula has two structurally equivalent 2º-carbons (next to the ends of the chain), and a structurally different 2º-carbon in the middle of the chain. A consideration of molecular symmetry helps to distinguish structurally equivalent from nonequivalent atoms and groups. The ability to distinguish structural differences of this kind is an essential part of mastering organic chemistry. It will come with practice and experience.

Our ability to draw structural formulas for molecules is remarkable. To see how this is done Click Here.

Analysis of Molecular Formulas

Although structural formulas are essential to the unique description of organic compounds, it is interesting and instructive to evaluate the information that may be obtained from a molecular formula alone. Three useful rules may be listed:

1. The number of hydrogen atoms that can be bonded to a given number of carbon atoms is limited by the valence of carbon. For compounds of carbon and hydrogen (hydrocarbons) the maximum number of hydrogen atoms that can be bonded to n carbons is 2n + 2 (n is an integer). In the case of methane, CH₄, n=1 & 2n + 2 = 4. The origin of this formula is evident by considering a hydrocarbon made up of a chain of carbon atoms. Here the middle carbons will each have two hydrogens and the two end carbons have three hydrogens each. Thus, a six-carbon chain (n = 6) may be written H-(CH₂)₆-H, and the total hydrogen count is (2 x 6) + 2 = 14. The presence of oxygen (valence = 2) does not change this relationship, so the previously described C₄H₁₀O isomers follow the rule, n=4 & 2n + 2 = 10. Halogen atoms (valence = 1) should be counted equivalent to hydrogen, as illustrated by C₃H₅Cl₃, n = 3 & 2n + 2 = 8 = (5 + 3). If nitrogen is present, each nitrogen atom (valence = 3) increases the maximum number of hydrogens by one.

Some Plausible Molecular Formulas	C7H16O3, C9H18, C15H28O3, C6H16N2
Some Impossible Molecular Formulas	C8H20O6, C23H50, C5H10Cl4, C4H12NO

2. For stable organic compounds the total number of odd-valenced atoms is even. Thus, when even-valenced atoms such as carbon and oxygen are bonded together in any number and in any manner, the number of remaining unoccupied bonding sites must be even. If these sites are occupied by univalent atoms such as H, F, Cl, etc. their total number will necessarily be even. Nitrogen is also an odd-valenced atom (3), and if it occupies a bonding site on carbon it adds two additional bonding sites, thus maintaining the even/odd parity.

Some Plausible Molecular Formulas	C4H4Cl2, C5H9OBr, C5H11NO2, C12H18N2FCl
Some Impossible Molecular Formulas	C5H9O2, C4H5ClBr, C6H11N2O, C10H18NCl2

3. The number of hydrogen atoms in stable compounds of carbon, hydrogen & oxygen reflects the number of double bonds and rings in their structural formulas. Consider a hydrocarbon with a molecular structure consisting of a simple chain of four carbon atoms, CH₃CH₂CH₂CH₃. The molecular formula is C₄H₁₀ (the maximum number of bonded hydrogens by the 2n + 2 rule). If the four carbon atoms form a ring, two hydrogens must be lost. Similarly, the introduction of a double bond entails the loss of two hydrogens, and a triple bond the loss of four hydrogens.

From the above discussion and examples it should be clear that the molecular formula of a hydrocarbon (C_nH_m) provides information about the number of rings and/or double bonds that must be present in its structural formula. By rule #2 must be an even number, so if m < (2n + 2) the difference is also an even number that reflects any rings and double bonds. A triple bond is counted as two double bonds.

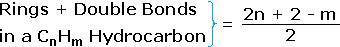
The presence of one or more nitrogen atoms or halogen substituents requires a modified analysis. The above formula may be extended to such compounds by a few simple principles:

• The presence of oxygen does not alter the relationship.
• All halogens present in the molecular formula must be replaced by hydrogen.
• Each nitrogen in the formula must be replaced by a CH moiety.

Resonance

Kekulé structural formulas are essential tools for understanding organic chemistry. However, the structures of some compounds and ions cannot be represented by a single formula. For example, sulfur dioxide (SO₂) and nitric acid (HNO₃) may each be described by two equivalent formulas (equations 1 & 2). For clarity the two ambiguous bonds to oxygen are given different colors in these formulas.

sulfur dioxide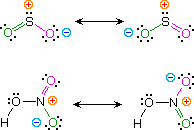
nitric acid

If only one formula for sulfur dioxide was correct and accurate, then the double bond to oxygen would be shorter and stronger than the single bond. Since experimental evidence indicates that this molecule is bent (bond angle 120º) and has equal length sulfur : oxygen bonds (1.432 Å), a single formula is inadequate, and the actual structure resembles an average of the two formulas. This averaging of electron distribution over two or more hypothetical contributing structures (canonical forms) to produce a hybrid electronic structure is called resonance. Likewise, the structure of nitric acid is best described as a resonance hybrid of two structures, the double headed arrow being the unique symbol for resonance.

The above examples represent one extreme in the application of resonance. Here, two structurally and energetically equivalent electronic structures for a stable compound can be written, but no single structure provides an accurate or even an adequate representation of the true molecule. In cases such as these, the electron delocalization described by resonance enhances the stability of the molecules, and compounds or ions composed of such molecules often show exceptional stability.

formaldehyde

The electronic structures of most covalent compounds do not suffer the inadequacy noted above. Thus, completely satisfactory Kekulé formulas may be drawn for water (H₂O), methane (CH₄) and acetylene C₂H₂). Nevertheless, the principles of resonance are very useful in rationalizing the chemical behavior of many such compounds. For example, the carbonyl group of formaldehyde (the carbon-oxygen double bond) reacts readily to give addition products. The course of these reactions can be explained by a small contribution of a dipolar resonance contributor, as shown in equation 3. Here, the first contributor (on the left) is clearly the best representation of this molecular unit, since there is no charge separation and both the carbon and oxygen atoms have achieved valence shell neon-like configurations by covalent electron sharing. If the double bond is broken heterolytically, formal charge pairs result, as shown in the other two structures. The preferred charge distribution will have the positive charge on the less electronegative atom (carbon) and the negative charge on the more electronegative atom (oxygen). Therefore the middle formula represents a more reasonable and stable structure than the one on the right. The application of resonance to this case requires a weighted averaging of these canonical structures. The double bonded structure is regarded as the major contributor, the middle structure a minor contributor and the right hand structure a non-contributor. Since the middle, charge-separated contributor has an electron deficient carbon atom, this explains the tendency of electron donors (nucleophiles) to bond at this site.

The basic principles of the resonance method may now be summarized.

For a given compound, a set of Lewis / Kekulé structures are written, keeping the relative positions of all the component atoms the same. These are the canonical forms to be considered, and all must have the same number of paired and unpaired electrons.
The following factors are important in evaluating the contribution each of these canonical structures makes to the actual molecule.

1. The number of covalent bonds in a structure. (The greater the bonding, the more important and stable the contributing structure.)
2. Formal charge separation. (Other factors aside, charge separation decreases the stability and importance of the contributing structure.)
3. Electronegativity of charge bearing atoms and charge density. (High charge density is destabilizing. Positive charge is best accommodated on atoms of low electronegativity, and negative charge on high electronegative atoms.)

The stability of a resonance hybrid is always greater than the stability of any canonical contributor. Consequently, if one canonical form has a much greater stability than all others, the hybrid will closely resemble it electronically and energetically. This is the case for the carbonyl group (eq.3). The left hand C=O structure has much greater total bonding than either charge-separated structure, so it describes this functional group rather well. On the other hand, if two or more canonical forms have identical low energy structures, the resonance hybrid will have exceptional stabilization and unique properties. This is the case for sulfur dioxide (eq.1) and nitric acid (eq.2).

carbon monoxide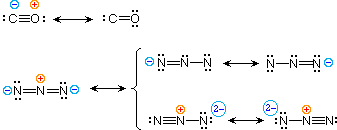
azide anion

To illustrate these principles we shall consider carbon monoxide (eq.4) and azide anion (eq.5). In each case the most stable canonical form is on the left. For carbon monoxide, the additional bonding is more important than charge separation. Furthermore, the double bonded structure has an electron deficient carbon atom (valence shell sextet). A similar destabilizing factor is present in the two azide canonical forms on the top row of the bracket (three bonds vs. four bonds in the left most structure). The bottom row pair of structures have four bonds, but are destabilized by the high charge density on a single nitrogen atom.

All the examples on this page demonstrate an important restriction that must be remembered when using resonance. No atoms change their positions within the common structural framework. Only electrons are moved.

Atomic and Molecular Orbitals

A more detailed model of covalent bonding requires a consideration of valence shell atomic orbitals. For second period elements such as carbon, nitrogen and oxygen, these orbitals have been designated 2_s, 2p_x, 2p_y & 2p_z. The spatial distribution of electrons occupying each of these orbitals is shown in the diagram below.

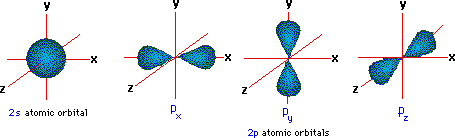
The valence shell electron configuration of carbon is 2_s², 2p_x¹, 2p_y¹ & 2p_z⁰. If this were the configuration used in covalent bonding, carbon would only be able to form two bonds. Very nice displays of orbitals may be found at the following sites: J. Gutow, Univ. Wisconsin Oshkosh, R. Spinney, Ohio State and M. Winter, Sheffield University

Hybrid Orbitals

In order to explain the structure of methane (CH₄), the 2s and three 2p orbitals must be converted to four equivalent hybrid atomic orbitals, each having 25% s and 75% p character, and designated sp³. These hybrid orbitals have a specific orientation, and the four are naturally oriented in a tetrahedral fashion.

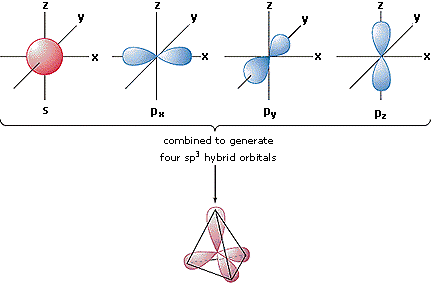
Molecular Orbitals

Just as the valence electrons of atoms occupy atomic orbitals (AO), the shared electron pairs of covalently bonded atoms may be thought of as occupying molecular orbitals (MO). It is convenient to approximate molecular orbitals by combining or mixing two or more atomic orbitals. In general, this mixing of n atomic orbitals always generates n molecular orbitals. The hydrogen molecule provides a simple example of MO formation. In the following diagram, two 1s atomic orbitals combine to give a sigma (σ) bonding (low energy) molecular orbital and a second higher energy MO referred to as an antibonding orbital. The bonding MO is occupied by two electrons of opposite spin, the result being a covalent bond.

The notation used for molecular orbitals parallels that used for atomic orbitals. Thus, s-orbitals have a spherical symmetry surrounding a single nucleus, whereas σ-orbitals have a cylindrical symmetry and encompass two (or more) nuclei. In the case of bonds between second period elements, p-orbitals or hybrid atomic orbitals having p-orbital character are used to form molecular orbitals. For example, the sigma molecular orbital that serves to bond two fluorine atoms together is generated by the overlap of p-orbitals (part A below), and two sp³ hybrid orbitals of carbon may combine to give a similar sigma orbital. When these bonding orbitals are occupied by a pair of electrons a covalent bond, the sigma bond results. Although we have ignored the remaining p-orbitals, their inclusion in a molecular orbital treatment does not lead to any additional bonding, as may be shown by activating the fluorine correlation diagram below.

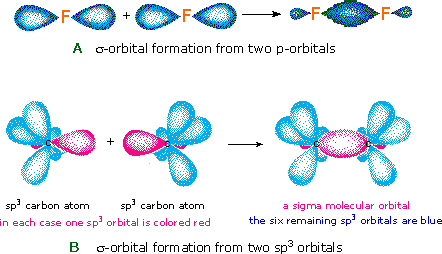
Another type of MO (the π orbital) may be formed from two p-orbitals by a lateral overlap, as shown in part A of the following diagram. Since bonds consisting of occupied π-orbitals (pi-bonds) are weaker than sigma bonds, pi-bonding between two atoms occurs only when a sigma bond has already been established. Thus, pi-bonding is generally found only as a component of double and triple covalent bonds. Since carbon atoms involved in double bonds have only three bonding partners, they require only three hybrid orbitals to contribute to three sigma bonds. A mixing of the 2s-orbital with two of the 2p orbitals gives three sp² hybrid orbitals, leaving one of the p-orbitals unused. Two sp² hybridized carbon atoms are then joined together by sigma and pi-bonds (a double bond), as shown in part B.

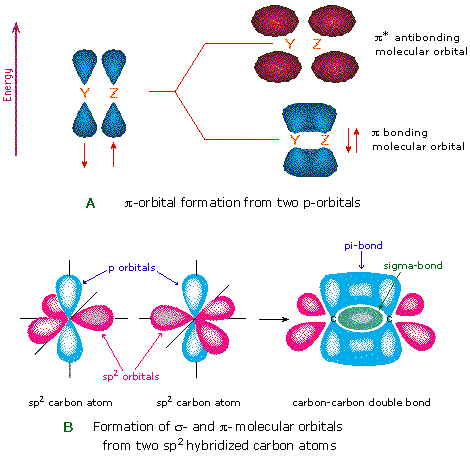
The manner in which atomic orbitals overlap to form molecular orbitals is commonly illustrated by a correlation diagram. Two examples of such diagrams for the simple diatomic elements F₂ and N₂ will be drawn above when the appropriate button is clicked. The 1s and 2s atomic orbitals do not provide any overall bonding, since orbital overlap is minimal, and the resulting sigma bonding and antibonding components would cancel. In both these cases three 2p atomic orbitals combine to form a sigma and two pi-molecular orbitals, each as a bonding and antibonding pair. The overall bonding order depends on the number of antibonding orbitals that are occupied.

The subtle change in the energy of the σ_2p bonding orbital, relative to the two degenerate π-bonding orbitals, is due to s-p hybridization that is unimportant to the present discussion. An impressive example of the advantages offered by the molecular orbital approach to bonding is found in the oxygen molecule. Click Here to see this application. The p-orbitals in this model are represented by red and blue colored spheres, which represent different phases, defined by the mathematical wave equations for such orbitals.

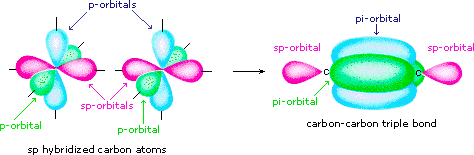
Finally, in the case of carbon atoms with only two bonding partners only two hybrid orbitals are needed for the sigma bonds, and these sp hybrid orbitals are directed 180º from each other. Two p-orbitals remain unused on each sp hybridized atom, and these overlap to give two pi-bonds following the formation of a sigma bond (a triple bond), as shown below.

Contributors

William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry