4.3: Rheology

Viscosity measurements are the realm of a field of science called rheology. Rheology is, literally, the study of flow. Another very simple definition, attributed to chemical engineer Chris Macosko at University of Minnesota, is the study of "what happens when you squish stuff". There's an element of force or pressure that comes into play here, too.

One of the common ways of assessing properties in rheology is to place a sample between two parallel plates and move one plate with respect to the other. One plate says still and the other one moves. What happens to the liquid between the plates? There ought to be some friction between the stationary plate and the liquid that will keep the liquid still. There also ought to be some friction between the moving plate and the liquid that will make the liquid move along at the same speed as that plate. So at one extreme, the liquid is moving along with the sliding plate and at the other extreme the liquid is perfectly still. If we imagine that the liquid in between these two extremes is divided into very thin layers, then each layer must be moving at a slightly different speed than the next.

In the diagram, the symbol, u, stands for the speed of the layer of liquid. The arrow beside the layer is meant to convey its relative speed: the top layer is moving the fastest, the next layer is a little slower, and so on; the bottom layer isn't moving at all. There is an important quantity, called the strain rate or shear rate (given as a symbol the Greek letter gamma, γ, with a dot on top) that describes how the speed of the liquid moving along the x-axis (left to right) changes, layer by layer, in the y-direction.

What does this picture have to do with viscosity? Well, in order to get that top plate to move, we have to apply some sort of force to it. In rheology the force is given per unit area (like pressure); this force per unit area is described as the stress (given as a symbol the Greek letter sigma, σ).

What if we wanted to slide the plate even faster? What would happen to the liquid? Well, the shear rate would go up. The top layer would be moving even faster, and the bottom layer would still be stationary. And what would we have to do to get that faster shear rate? We would have to push the top plate a little harder. The result is a graph that looks like this:

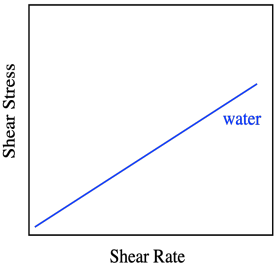
The graph says that shear stress and shear rate are directly related. The stress is called "shear stress" because of the direction of the force parallel to the liquid, causing shear strain. When we increase the shear rate, the shear stress also increases proportionally. So, if we did this experiment using water as the liquid between the plates, we would get a linear relationship between shear stress and shear rate. That's how Sir Isaac Newton described the behavior of liquids, so when we see that linear relationship between stress and strain, we describe the liquid as a Newtonian liquid.

What happens if we do the experiment with honey instead of water? What would happen, for example, if we exerted a certain stress to get a certain shear rate with the water, and we wanted to get the same shear rate using honey? Well, the honey is thicker than the water. It's not going to move as easily. We will have to apply a greater stress in order to achieve the same shear rate that we measured with water.

That would be true for every possible shear rate. If we were to graph shear stress vs. shear strain with honey, we would get a linear relationship, just like we did with water, but the value of shear stress would always be higher than for water. The slope of the line for honey would be greater than the slope of the line for water.

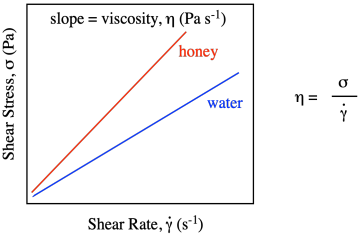
Viscosity is formally defined as the slope of that line. Honey, being thicker than water, requires higher and higher stresses to achieve the same strain rates that you would get using lower stresses with water. In the simple kitchen analog of the experiment, you have to push the spoon harder to stir the honey than you do if you are just stirring water.

Honey and water are Newtonian liquids. The relationship is simple: increase the shear stress and you increase the shear rate. Not all liquids behave that way. Polymer solutions don't, for example. They display a non-linear relationship, in which the shear stresses needed to get higher shear rates are just not as high as you would expect.

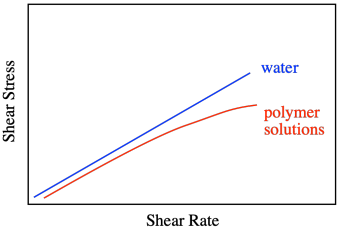
That behavior is described as shear thinning. What makes polymer solutions do that? Remember that, in solution, an individual polymer molecule tends to coil up into a ball. Normally, those balls are spherical. At high shear rates, they distort into ellipses. That reduces the amount of drag, making the solution a little less viscous than you would expect. The shear stress still increases with higher shear rates, but not as much as if it were a Newtonian fluid.

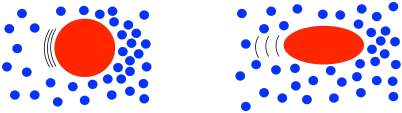
That's not all. Remember, polymers display chain entanglement, especially when they are very large. Chain entanglement increases the viscosity of the solution. These chains are mobile because the polymer is constantly undergoing conformational changes. As the solution gets sheared, some of the polymer chains may wiggle loose from their neighbors, but random conformational changes will always result in new entanglements right away.

But what happens at a very high rate of shear strain? The polymer chains still become untangled, but they don't have time to form new entanglements, because everything is whizzing by too quickly. Without those entanglements, viscosity doesn't increase as sharply as you would expect.

Some liquids behave just like water, but polymer solutions do not. That's a consequence of the enormously long chain structures of the polymers. It's worth pointing out that there are other things that don't behave in the "normal" way. Colloids often display shear thickening. You can see examples of this in videos of people running across wading pools filled with corn starch and water, a colloidal mixture in which the solid cornstarch particles are just suspended in the water, not dissolved. If you walk across the pool, you sink. If you run, you stay on top. That's shear thickening, and it has to do with how those solid particles move during shearing. When you walk, they just slide past each other, but when you run, they all collide, and come to a stop.

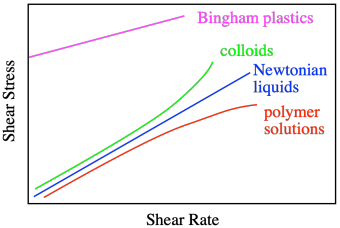
A Bingham plastic, on the other hand, actually appears to be a solid until you give it a good shove; then it flows like a liquid. Peanut butter behaves sort of like that.

Exercise 4.3.1

Honey is a Newtonian fluid, but molasses undergoes shear thinning. What might you deduce about the composition of molasses and honey?