3.4: Kinetics of Catalytic Polymerization

Last updated
Save as PDF

Page ID: 238868

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

KP4. Kinetics of Catalytic Polymerization

The Ziegler-Natta polymerization of alkenes is conducted under catalytic conditions. In most cases, the process involves heterogeneous catalysis, in which the reaction takes place on the surface of a solid. The kinetics of catalyzed reactions have some features that are different from other reactions and that are worth exploring.

The fact that the reaction is taking place on the surface of a solid is a key feature that must be stressed in the kinetics of heterogeneous catalysis. The treatment of rates therefore uses an approach developed by Irving Langmuir, a long-time scientist at General Electric who was awarded the Nobel Prize for the study of surfaces. One of the things that makes metal catalysts so useful is their ability to adsorb molecules on their surfaces (think of the precious metals used in catalytic hydrogenation, adsorbing alkenes and hydrogen; or the iron in the Haber-Bosch synthesis of ammonia, adsorbing dinitrogen and hydrogen, to cite two important examples). "Adsorption" refers to the adhesion of molecules to a surface. Langmuir thought of this adsorption process as a dynamic one, with molecules landing on and sticking to open spots on a surface even as other molecules lifted off to create vacancies.

Desorption, on the other hand, refers to the process of molecules leaving the surface.

In terms of kinetics, the rate of desorption of a molecule would depend on some rate constant, k_d, and the fraction of the surface covered by these molecules, θ (that's the Greek letter, theta). The greater the surface fraction covered by molecules, the greater the chance that you will encounter one desorbing.

Rate_d = k_dθ

On the other hand, the rate os adsorption of a molecule onto a surface will depend on some rate constant k_a, the concentration of the molecule to be adsorbed, and the fraction of the surface still available. That last part is 1 - θ, because the fraction covered plus the fraction uncovered would equal the whole. Note that Langmuir was interested in gas phase molecules adsorbing onto a surface, and so he expressed things in terms of pressure rather than concentration.

Rate_a = k_a (1 - θ) [M]

At equilibrium, these two rates will equal each other:

k_d θ = k_a [M] - k_a θ [M]

θ (k_d + k_a [M]) = k_a [M]

θ = k_a [M] / (k_d + k_a [M])

Now we have an expression for the fraction of the surface covered by the substrate. This term is called the "Langmuir isotherm" and it shows up in various surface and catalytic phenomena. It is usually expressed slightly differently, in terms of an equilibrium constant for adsorption:

The rate of a reaction catalyzed on that surface will depend on the catalyst concentration as well as a rate constant for enchainment, k_prop or simply k_p, and the amount of surface covered by monomer (unbound monomer will not undergo propagation). An additional factor, x*, takes into account the fact that only a fraction of the catalyst is active.

Superficially, the form of the rate law has something in common with the Michaelis-Menten equation, with which you may already be familiar. The Michaelis-Menten equation relates the rate of an enzyme-catalyzed reaction to enzyme concentration, the rate constant for the catalytic reaction, and rate constants for reversible substrate binding with the enzyme.

Maybe that resemblance shouldn't be too surprising. After all, both equations describe catalytic processes, in which either the surface or the binding site must accomodate the substrate so as to carry out a subsequent series of reactions. Both equations take the form of a saturation curve, indicating that the rate of reaction will level out if the surface or binding site becomes fully occupied.

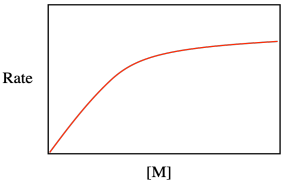
Problem KP4.1.

One way to evaluate multi-term relationships is to consider what happens under different conditions. What happens to the rate law for catalytic polymerization if monomer concentration is very low, so that 1 >> K_eq[M]?

Problem KP4.2.

What happens to the rate law for catalytic polymerization if monomer concentration is very high, so that K_eq[M] >> 1?