3.2: Kinetics of Step-Growth Polymerization
- Page ID
- 238865
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)KP2. Kinetics of Step-Growth Polymerization
It is important to understand how reactions proceed over time. This information can tell us how long it will take for a polymer to reach an optimum length. It can also provide insight into how the polymerization occurs, just as kinetics can provide insight into other reaction mechanisms.
Condensation polymers grow through a a step-growth process. The reaction generally involves substitution at a carboxyloid. For example, polyester formation often involves the substitution of an alcohol functional group at a carboxylic acid, making an ester. The drawing below illustrates that action using ethylene glycol and oxalic acid, to use common names prevalent in industry. Oxalic acid is not typically used in making polyesters, but it is drawn here as a very simple example structure.

If you know some basic kinetics, you know that we can express the rate of a reaction as the rate of change of product concentration per change in time. In this case, the product is the polymer, abbreviated P. Alternatively, we could express the rate of the reaction as the rate of change of monomer concentration per change in time. Just by looking at the equation of reaction, we expect that every time a polymer molecule is made, a monomer molecule is used up. In this case, we have a co-polymer, made of two different monomers, so that's why we could express the reaction rate as the rate of change of either monomer concentration. The negative sign in the rate suggests we are looking at the rate of disappearance of monomer; as polymer appears, monomer disappears.
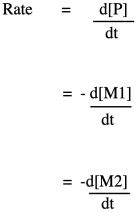
If you know something about organic reaction mechanisms, you may know that the very first step in an esterification is the donation of a lone pair from an alcohol oxygen on the diol to a carbonyl carbon on the dicarboxylic acid. (It could actually be the second step, but we'll get to that later.) That first step in the mechanism is an elementary reaction. All of the other steps you would draw in a mechanism are also elementary reactions. The nice thing about elementary reactions is that we always know the rate law of each one: it's a rate constant times the concentrations of all of the species leading into that step. In this case, this first step is also the rate-determining step, so the entire reaction is governed by the rate law of that first step. It requires both monomers, so we get a simple rate law.
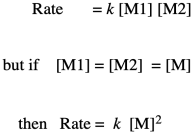
Note that, based on the stoichiometry (the ratio of monomers in the equation of reaction), we would probably run this polymerization with equal amounts of diol and dicarboxylic acid. Instead of worrying about M1 and M2 separately, we can call them both [M].
So, what we have here is a simple second-order rate law. This form of the rate law is called the differential rate law, because it is expressed in terms of the rate of change of one thing with the rate of change of the other. If that isn't exactly what you are interested in, and you just want to see what happens to concentrations over time, you may want to integrate this expression to obtain the integrated from of the rate law.
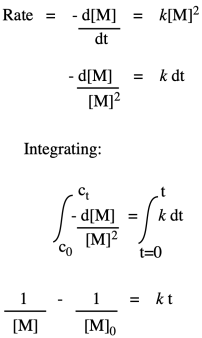
If we were to measure monomer concentration periodically during the polymerization and plot its inverse over time, we would obtain a straight line. The slope of the line would be the rate constant, and the intercept would reflect the inverse of the monomer concentration with which we had started the reaction.
At this point, we need to pause and talk about what we actually mean by monomer concentration. Because of a very specific feature of condensation polymerizations, it isn't really the concentration of ethylene glycol or oxalic acid. Take a look at this drawing of this step-growth process and we will talk about why that is.
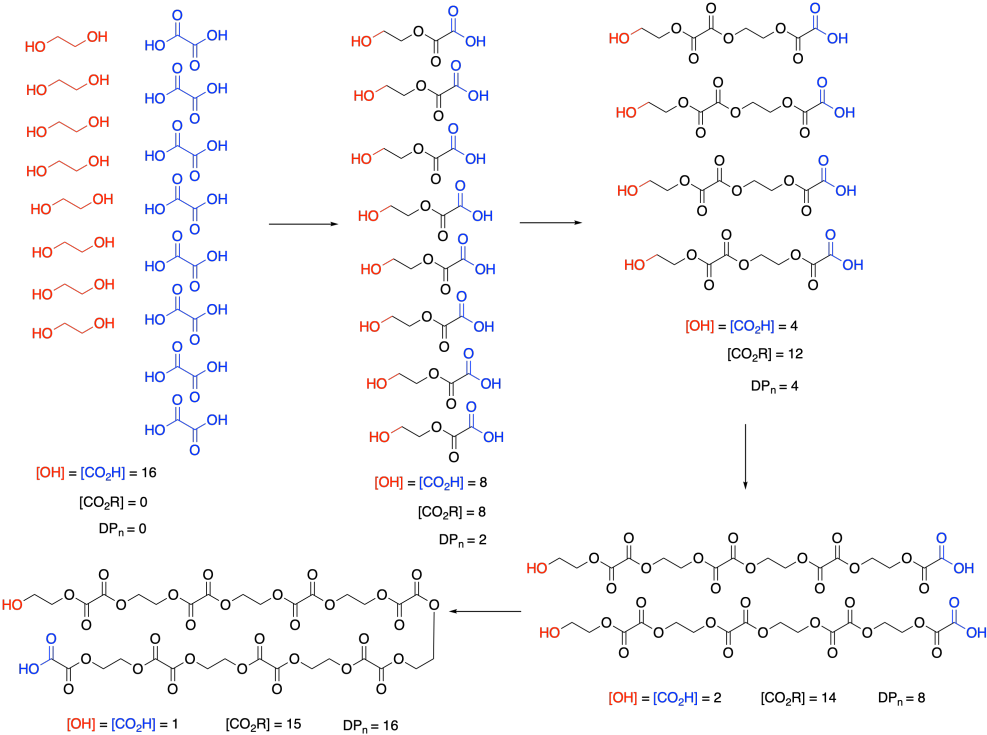
Remember that, in step-growth polymerization, the majority of molecules are probably reacting at roughly similar rates. Two monomers link together to form dimers, two dimers form tetramers, two tetramers form octamers, and so on. It won't go as perfectly as we see in this picture; there will inevitably be some stragglers that throw the averages off. But notice what this means: the monomers disappear right away. Nobody is really interested in how quickly the monomers turn into dimers. They want to know how the gowth of the polymer chain is progressing.
So, in the above expression, [M] doesn't refer to the concentrations of those two monomers at all. It refers to the concentration of the reactive functional groups in those monomers. After all, once the monomers are gone, the same esterification reaction keeps happening, and it's really the concentration of alcohol and carboxylic acid groups that matters, whether they are found on monomers, dimers, tertramers, or whatever. In these rate expressions, sometimes people will explicitly use [OH] and [CO2H] in the rate expression, underscoring that they are really following the disappearance of those functional groups.
And notice what's happening to those functional groups. Their concentration is smoothly dropping over time. Furthermore, ester concentration, representing the new functional group in the polymer, is growing in at the same rate. [OH] and [CO2H] drop by 8 (or in half) in the first step; [CO2R] increases by 8, and so on. SO the rate of consumption of reactant functional groups equals the rate of appearance of product functional groups.
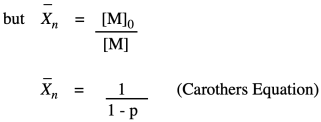
The other thing we are interested in here is the degree of polymerization: the number of monomers incorporated into the chain. The polymer is growing at a certain rate, but how long is it getting? Just looking at the simple scheme of polymer growth above, we see the average degree of polymerization increasing (written as DP or sometimes as Xn; a bar over the symbol signals that we are looking at an average). If you look carefully, you will see that the degree of polymerization is always the original monomer concentration divided by the remaining monomer concentration. That turns out to be a very important relationship.

Note that this relationship is just the inverse of the fraction of monomer remaining (or, really, the fraction of those monomer functional groups left over).
![]()
The opposite quantity is the fraction of monomer converted. That describes the functional groups already converted into esters. Because we are dealing with fractions, the fraction converted is just one minus the fraction remaining. If we do a little algebra, we get a variation on that piece of information.

Why did we do that last part? Because now we have arrived back at the expression for degree of polymerization. So, now we have an equivalent way of expressing degree of polymerization in terms of the fraction converted. This relationship is called the Carothers equation, in honor of Wallace Carothers, the DuPont chemist who invented nylon.
Problem KP2.1.
Predict the degree of polymerization if 75% of monomer end groups have been converted to polymer.
So, what does that relationship look like? Here's some data from Paul Flory, another DuPont chemist and Nobel laureate, obtained during the period between the World Wars when this kind of chemistry was just getting started (Flory, P. J. J. Am. Chem. Soc. 1937, 59, 466-470).
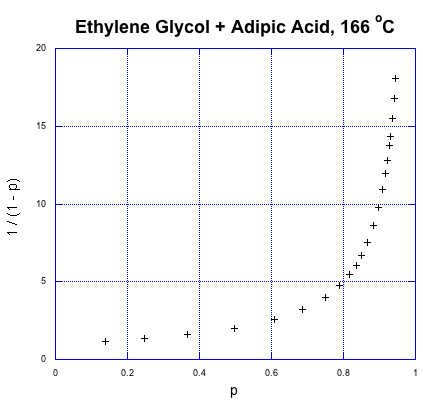
That's fraction converted on the x axis and the expression for degree of polymerization on the y axis. This is exponential growth. The degree of polymerization is starting to shoot upward dramatically. We already knew that from our introduction to step growth, but what stands out from the data is how a higher degree of polymerization, and high molecular weight, doesn't really occur until very late in the reaction. If we need high molecular weight condensation polymers, the chemistry better be pretty reliable; otherwise, if things go wrong, we'll be left with some short-chain goo instead of long-chain materials.
Now let's take these new relationships and look at them in the context of our second-order kinetics. We're starting with that same integrated rate law, but we have mulitplied everything on both sides of the equation by the starting monomer concentration. That's fair game in algebra, remember. The reason for doing that is to get a term that resembles our relationships that describe degree of polymerization.
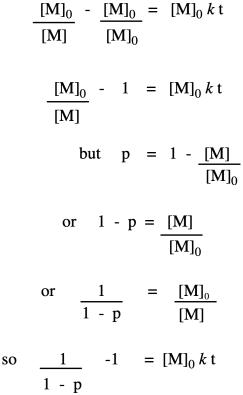
So far, we have taken the ratio we obtained in the first line and worked out its relationship to fraction converted, which we substituted in the last line. Now we bring in the Carothers equation to recall that this is really telling us how degree of polymerization changes over time. This relationship indicates the degree of polymerization should increase linearly over time.
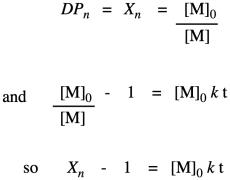
This relationship indicates the degree of polymerization should increase linearly over time. Once again, we're going to use Flory's data to illustrate the relationship, using the fraction conversion data. He could measure that data easily, and knew how it was related to degree of polymerization.
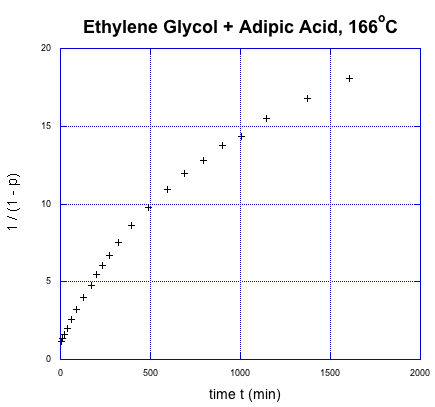
It was supposed to be linear. But don't worry; Flory knew what went wrong. You might know, too, if you remember a few things about substitution at carboxloids. The trouble is, we are dealing with a neutral nucleophile and a fairly unreactive electrophile. That reaction should be really slow. It isn't that slow, thoough, because it is self-catalyzed. One carboxylic acid monomer can activate another, making it a better electrophile.

That means the coupling of the alcohol with the carboxylic acid isn't the first elementary step of the reaction, but the second. Before the alcohol and carboxylic acid can come together, two carboxylic acids need to have collided already. That means we have a third order reaction. As it happens, the integrated form of a third order rate law isn't all that much more complicated, and we can do some similar algebra with it to see how the degree of polymerization would vary with time given this new information.
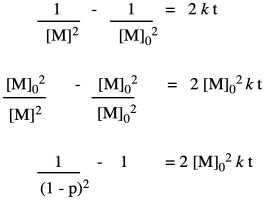
We can take Flory's data again and give it this new treatment.
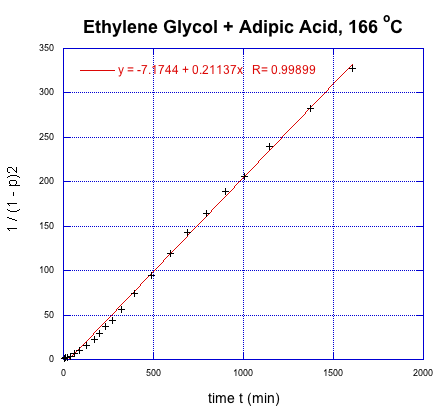
This time, we get a linear relationship. That correction illustrates one of the fundamental uses of kinetics, which is a tool that lets us probe how reactions happen. In this very specific case, kinetics showed that there was an extra (pre-rate determining) step in the reaction. In addition, we found that it is the square of the degree of polymerization that is increasing linearly with time.
Problem KP2.2.
Given an initial alcohol group concentration [M]0 = 17 M, determine the rate constant from Flory's data in L2mol-2s-1.
Flory also established a statistical basis for predicting molecular weights and molecular weight distributions in polymers. For example, once we have the degree of polymerization, it is a simple step to calculate the approximate molecular weight. That's just the degree of polymerization times the molecular weight of the monomer; in other words, the number of monomers in the chain times the weight of each one. (This approach neglects any small molecules such as water that are lost during the condensation reaction.)
Mn = DP x M0
Mn = M0 / (1 - p)
This is called the number average molecular weight. It's based on taking one average value for the chain length and converting that into the chain molecular weight. Of course, some chains may be much shorter (Flory actually shows, based on probability, that there will be a number of monomers left over) and as such they contribute less to the overall sample.
A second way to approach the average chain molecular weight is to assess the fraction of the total weight contributed by each chain length. The average chain molecular weight would then be given by:
Mw = Σ πxxM0
in which πx is the fraction of chains of length x.
What is the fraction of chains of length x? The approach starts with considering the probability that a chain will be x units long. As noted above, a chain x units long has x-1 ester linkages and 2 unreacted chain ends. We know the probability of a chain end being converted to a polymer linkage is p, and in a chain x units long that will have to happen x-1 times, for a probability px-1. We also know that the probability of a functional group being left unreacted is 1-p, and that has to happen twice here, for a probability (1-p)2. The probability of having a chain of length x is:
πx = x px-1(1-p)2
That means:
Mw = Σ x px-1(1-p)2 xM0
Mw = (1-p)2M0 Σ x2 px-1
The series on the right is reducible to:
Σ x2 px-1 = (1 + p) / (1 - p)3
So that:
Mw = (1-p)2M0(1 + p) / (1 - p)3
Mw = M0(1 + p) / (1 - p)
That provides a straightforward prediction of the weight-average molecular weight based on the fraction converted in condensation polymerization. Although Mn and Mw presented here are essentially theoretical predictions of molecular weight, these quantities can also be measured experimentally using different methods.
The ratio between these two quantities has always been used as an expression of the breadth of the molecular weight distribution, called the polydispersity index or simply the dispersity:
D = Mw/Mn
In the case of condensation polymerization,
D = [M0(1 + p) / (1 - p)]/[M0 / (1 - p)]
D = 1 + p
Because p is always a fraction, the result is that the dispersity of a condensation polymerization is statistically expected to be less than 2.0.
Problem KP2.3.
Given 99% conversion of monomers with average molecular weight 120 g/mol, calculate Mw, Mn and D.


