3.1: Thermodynamics of Polymerization
- Page ID
- 238864
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Polymerization is the process of taking individual monomers and enchaining them into a macromolecule. Thermodynamically, there are always two factors to consider in a reaction: enthalpic contributions and entropic contributions.
\[ΔG = ΔH - TΔS \nonumber\]
Entropic changes in chain polymerizations tend to be qualitatively similar in different cases. Because a large number of monomers are being enchained together in a macromolecule, the number of degrees of freedom is always decreasing, regardless of the specific polymerization process under consideration. Consequently, the entropy change associated with polymerization is always negative.
\[ΔS = k_B \ln \left(\dfrac{W_f}{W_i} \right) \nonumber\]
in which \(k_B\) is Boltzmann's constant and \(W\) is the number of microstates available in the final or initial state. If \(W_f < W_i\), then \(ΔS < 0\) because the natural log of a fraction is a negative number.
Free energy correlates positively with enthalpy and negatively with entropy. That means that a negative entropy change translates into a positive, and unfavorable, free energy change. Polymerization is always entropically disfavored, regardless of the circumstances. However, because entropy changes are generally rather small compared to enthalpy changes, polymerization proceeds despite this handicap. The entropy factor begins to dominate the equation only at higher temperatures, because the entropy contribution scales with temperature (in Kelvin) in the expression for free energy.
As a result, thermodynamically, chain polymerizations should be run under cooler conditions in order to maximize the degree of polymerization. Nevertheless, there are certain polymerizations (such as ring-opening polymerization of cyclic esters) that are frequently run at elevated temperatures because of a significant barrier to the reaction. Of course, in these cases there tends to be a maximum extent of polymerization before the process bottoms out in an equilibrium between polymer and monomer.
In general, this entropic problem in entropy gives rise to the term "ceiling temperature", which is the temperature above which polymerization of a particular monomer will not occur.
In condensation polymerizations, the entropy of reaction is more subtle. The formation of condensation side products, such as water or methanol, means that there are not overall changes in the number of molecules before and after polymerization. For example, n co-monomers are converted into 1 polymer chain and n-1 water molecules. There may still be entropy changes in the reaction, but the sign of the entropy change is not as easy to predict compared to chain polymerization.
Since the entropy for chain polymerizations is always positive, then all chain polymerizations must be exothermic, because otherwise they would never proceed. The reasons for these enthalpically-favored reactions varies from one case to another.
In olefin polymerization (alkene polymerization), the enthalpy of reaction has been measured in a wide range of cases; it is usually around -20 kcal/mol. This negative ΔH value can be partly attributed to the exchange of one C=C π bond for one C-C σ bond for every alkene monomer enchained. The strength of an average C=C double bond is approximately 147 kcal/mol, whereas the strength of an average C-C bond is about 83 kcal/mol. By difference, the strength of a C=C π bond is about 64 kcal/mol. Thus, it costs 64 kcal/mol to break the π bond but we drop 83 kcal/mol for each σ bond made, for a net decrease of around 20 kcal/mol.
| Bond | Bond Energy (kcal/mol) | Bond | Bond Energy (kcal/mol) | Bond | Bond Energy (kcal/mol) |
|---|---|---|---|---|---|
| C-C | 83 | C-N | 73 | C=C | 147 |
| C-O | 86 | C-Cl | 81 | C=O | 178 |
| N-H | 93 | Cl-H | 102 | O-H | 111 |
To be sure, there are other factors that contribute to the enthalpy change. C-H bond strengths change significantly with hybridization changes. Intramolecular steric interactions are drastically different in standard monomers compared to polymers. In alkene polymerization in particular, phase changes between gas phase or liquid phase starting material and solid product is appreciable, although still small compared to the bond strength issues. Nevertheless, at first glance we would expect a moderately exothermic reaction, and that's what has been measured experimentally.
Diels Alder polymerization depends on a [4+2] cycloaddition. Thermodynamic studies on the parent reaction indicate ΔH = -40 kcal/mol. Explain this observation in terms of bond strengths.
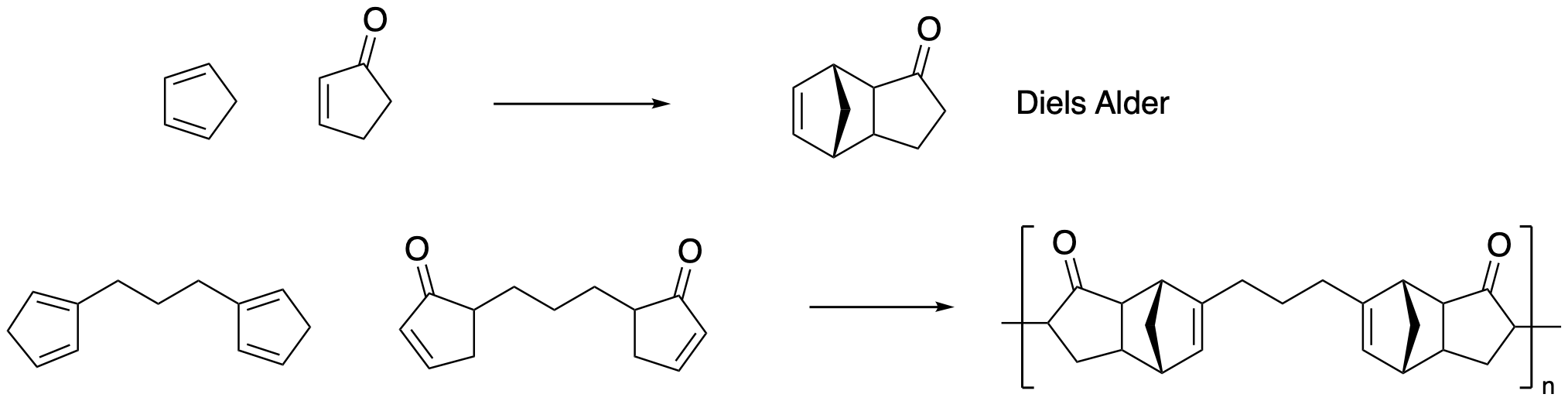
Taking a second example, the ring-opening polymerization of cyclic esters is considered to be exothermic because of ring strain. Values of ΔH are strongly dependent upon ring size, which is intimately connected with ring strain. For γ-butyrolactone, a five-membered ring containing a carbonyl, ΔH = -1 kcal/mol; that's not enough to compensate for a negative entropy of reaction, so that this monomer can only be polymerized at low temperatures. On the other hand, for δ-valerolactone, ΔH = -3 kcal/mol, whereas for ε-caprolactone, ΔH = -7 kcal/mol. These six- and seven-membered lactones are much more readily polymerized because of increasing ring strain.
The Ceiling temperature can be calculated from an assumption that \(ΔG = 0\), at which point polymerization is readily reversible. A kinetic approach to equilibrium gives the relation:
\[T_c = \dfrac{ΔH}{ΔS + R\log[M]} \nonumber\]
in which \(R\) is the ideal gas constant, 1.98 cal K-1 mol-1 (or 8.314 J K-1 mol-1)
Calculate the ceiling temperature for caprolactone polymerization if ΔH = -7 kcal mol-1 and ΔS = -8.6 cal K-1 mol-1. The concentration of neat caprolactone is 8.7 M. (Data from: Olsen, P.; Odelius, K.; Albertsson, A.-C. Biomacromolecules 2016, 17, 699-719.)
Given a less pronounced entropic bias against condensation polymerization, endothermicity becomes less crucial. Indeed, some condensation polymerizations are effected through simple trans-esterifications, which ought to be close to thermoneutral. As pointed out in the condensation section, these reactions are frequently driven to completion by removal of the condensation side product, small molecules such as methanol or water.
Some polyamides are made industrially from the corresponding difunctional amines and acid chlorides, releasing \(\ce{HCl}\). Calculate the enthalpy change for this reaction


