3.4E: Quantitating Crystallization
- Page ID
- 95759
In this section, real solubility data for compounds is used to quantitatively describe the purification of impure solids that contain either a "soluble impurity" or an impurity with similar solubility to the compound of interest.
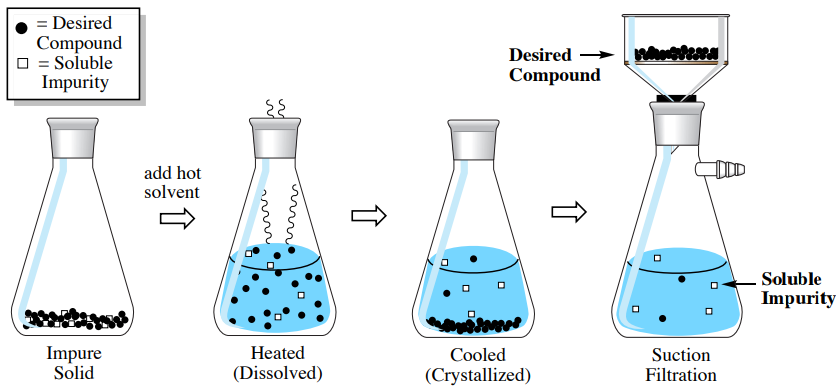
With a "Soluble Impurity"
The simplest crystallization in terms of purification is when an impurity is very soluble in the cold solvent while the compound of interest is not (see procedural sequence in Figure 3.27). In this situation, the impurity is trapped in the crystal matrix of the impure solid, and needs only be liberated by dissolution. After adding hot solvent to dissolve the impure solid then cooling, the soluble impurity remains dissolved in the mother liquor while the compound of interest crystallizes and can be collected by suction filtration.
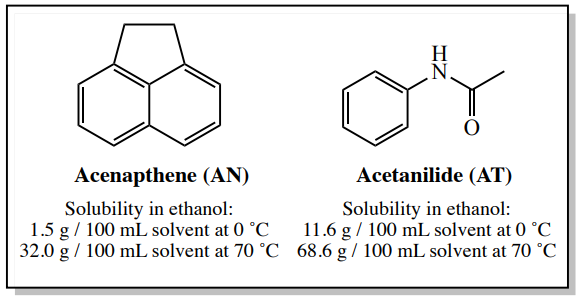
An example of this type of system is a sample containing \(4.00 \: \text{g}\) acenapthene and \(0.50 \: \text{g}\) acetanilide. According to Perrin's Purification of Organic Compounds,\(^9\) acenapthene can be purified by crystallization using ethanol, and even though this sample contains a considerable quantity of acetanilide impurity (\(13 \: \text{mol}\%\)), the calculations in this section will show that this process should work well.
The solubility values of acenapthene and acetanilide in ethanol are shown in Figure 3.28.
\(4.00 \: \text{g}\) of pure acenapthene (AN) should completely dissolve in \(12.5 \: \text{mL}\) (see calculation below) of nearly boiling ethanol (the boiling point of ethanol is \(78^\text{o} \text{C}\)).\(^{11}\)
\[4.00 \: \text{g Acenapthene (AN)} \times \frac{100 \: \text{mL hot ethanol}}{32.0 \: \text{g AN}} = \textbf{12.5 mL hot ethanol} \: \left( 70^\text{o} \text{C} \right) \: \text{to dissolve}\]
Since acetanilide (AT) is more soluble than acenapthene at this temperature (see Figure 3.28), it should also completely dissolve in \(12.5 \: \text{mL}\) of hot ethanol.
If the hot ethanolic solution containing these two components is then cooled in an ice bath, acenapthene should crystallize as it has low solubility in cold ethanol. The calculation below shows how much acenapthene would remain dissolved in the cold ethanol \(\left( 0.19 \: \text{g} \right)\). Any quantity of acenapthene present greater than \(0.19 \: \text{g}\) would form a solid, in this case \(3.81 \: \text{g}\) \(\left( 4.00 \: \text{g} - 0.19 \: \text{g} \right)\).
\[12.5 \: \text{mL cold ethanol} \times \frac{1.5 \: \text{g acenapthene (AN)}}{100 \: \text{mL cold ethanol}} = \textbf{0.19 g AN} \: \text{remains dissolved in} \: 0^\text{o} \text{C} \: \text{ethanol}\]
The acetanilide impurity, however, should not crystallize. The calculation below shows that \(1.45 \: \text{g}\) of acetanilide can dissolve in the cold ethanol, and since only \(0.50 \: \text{g}\) was originally present, the entire portion would remain dissolved.
\[12.5 \: \text{mL cold ethanol} \times \frac{11.6 \: \text{g AT}}{100 \: \text{mL cold ethanol}} = \textbf{1.45 g AT} \: \text{can dissolve in} \: 0^\text{o} \text{C} \: \text{ethanol}\]
This process is summarized in Figure 3.29. As only the acenapthene crystallizes, it could be collected through filtration and separated from the acetanilide impurity in the mother liquor.
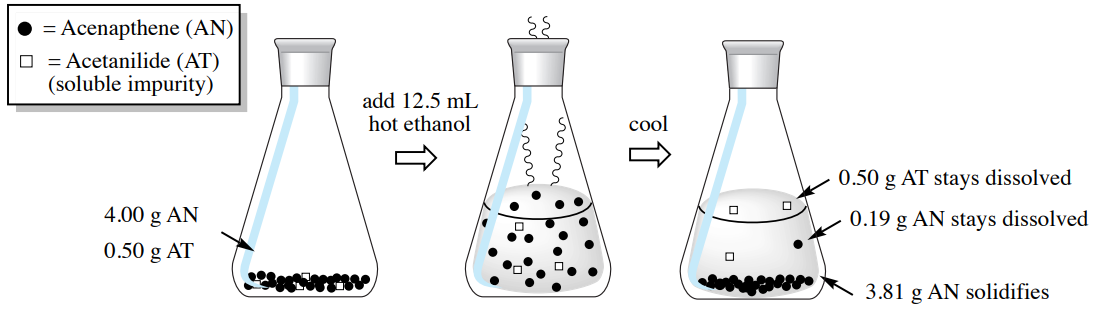
Purification of this mixture works well in theory because the acetanilide is so much more soluble (approximately ten times as much) in the cold ethanol than the acenapthene, and so can be removed. In practice if the crystallization is done too quickly, there is still the possibility of acetanilide being incorporated into the developing solid.
With an Impurity of Similar Solubility
If an impure solid contains an impurity that has similar solubility properties as the desired compound, it is still possible to purify the mixture through crystallization if the impurity is present in a small amount. An example is a sample containing \(4.00 \: \text{g}\) acenapthene and \(0.30 \: \text{g}\) phenanthrene (phenanthrene is \(6 \: \text{mol}\%\) of the sample). The solubility of these compounds in ethanol is shown in Figure 3.30.
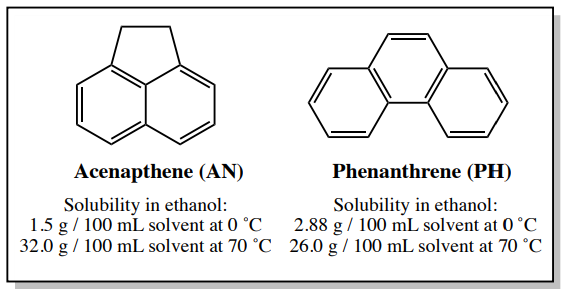
\(4.00 \: \text{g}\) of pure acenapthene (AN) should completely dissolve in \(12.5 \: \text{mL}\) (see calculation below) of nearly boiling ethanol (the boiling point of ethanol is \(78^\text{o} \text{C}\). \(0.30 \: \text{g}\) of pure phenanthrene (PH) would dissolve in \(1.2 \: \text{mL}\) of hot ethanol (see calculation below), and so would also dissolve in \(12.5 \: \text{mL}\) were used.
\[4.00 \: \text{g Acenapthene (AN)} \times \frac{100 \: \text{mL hot ethanol}}{32.0 \: \text{g AN}} = \textbf{12.5 mL hot ethanol} \: \left( 70^\text{o} \text{C} \right) \: \text{to dissolve AN}\]
\[0.30 \: \text{g Phenanthrene (PH)} \times \frac{100 \: \text{mL hot ethanol}}{26.0 \: \text{g PH}} = \textbf{1.2 mL hot ethanol} \: \left( 70^\text{o} \text{C} \right) \: \text{to dissolve PH}\]
If this hot solution is then cooled in an ice bath, the calculations below show the quantity of each compound that would remain dissolved in the cold ethanol.
\[12.5 \: \text{mL cold ethanol} \times \frac{1.5 \: \text{g acenapthene (AN)}}{100 \: \text{mL cold ethanol}} = \textbf{0.19 g AN} \: \text{remains dissolved in} \: 0^\text{o} \text{C} \: \text{ethanol}\]
\[12.5 \: \text{mL cold ethanol} \times \frac{2.88 \: \text{g phenanthrene (PH)}}{100 \: \text{mL cold ethanol}} = \textbf{0.360 g PH} \: \text{remains dissolved in} \: 0^\text{o} \text{C} \: \text{ethanol}\]
Since greater than this quantity of acenapthene is present, most of it will crystallize \(\left( 3.81 \: \text{g} \right)\). However, since only \(0.30 \: \text{g}\) of phenanthrene is present, the entire portion should remain in the mother liquor. The two components can then be separated through filtration.
In essence, impurities that have a similar solubility to the compound of interest can be removed like soluble impurities as long as they are present in small enough quantities. It is a general guide that solids containing less than \(5 \: \text{mol}\%\) of impurity can be purified in this manner. The crystallization process essentially "sacrifices" a portion of each component to the mother liquor in order to produce a pure crystal.
\(^9\)D.D. Perrin, W.L.F. Armarego, Purification of Organic Chemicals, Pergamon Press, 3\(^\text{rd}\) edition, 1988.
\(^{10}\)Adapted from data found in: A. Seidell, Solubilities of Inorganic and Organic Substances, D. Van Nostrand Company, 1907.
\(^{11}\)It is very possible that the acenapthene/acetanilide mixture might require a slightly different quantity of hot ethanol to dissolve than pure samples, but the calculations in this section provide a rough estimate of the solvent volumes needed.
\(^{12}\)Adapted from data found in: A. Seidell, Solubilities of Inorganic and Organic Substances, D. Van Nostrand Company, 1907.


