9.1: Some Important Concepts in Stereochemistry
- Page ID
- 215735
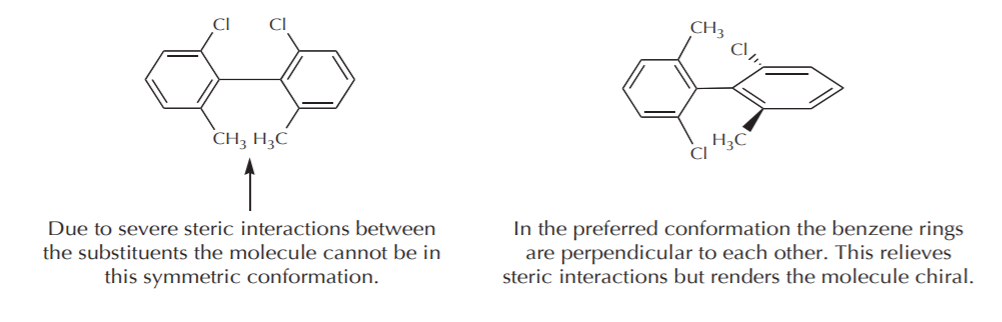
1. RELATIONSHIP BETWEEN SYMMETRY AND CHIRALITY
Asymmetric objects are chiral
Symmetric objects are achiral
2. RELATIONSHIP BETWEEN OBJECTS AND THEIR MIRROR IMAGES
Symmetric objects are superposable with their mirror images. They are one and the same. Asymmetric objects are nonsuperposable with their mirror images. They are different objects. In the case of molecules, chiral molecules and their mirror images are different molecules. Chiral molecules and their mirror images are a kind of stereoisomers called enantiomers.
3. DEFINITIONS
Stereoisomers - Compounds that have the same molecular formula and the same connectivity, but different arrangement of the atoms in 3-dimensional space. Stereoisomers cannot be converted into each other without breaking bonds.
Enantiomers - Nonsuperposable mirror images, or chiral molecules which are mirror images.
Chiral, or asymmetric carbon - A tetrahedral carbon atom bearing four different substituents.
Chirality centers, or stereocenters - Asymmetrically substituted atoms in a molecular structure. The most common type encountered in this course will be the chiral carbon described above.
Diastereomers - Stereoisomers which are not enantiomers (or mirror images).
Meso compounds, or meso forms - Symmetric, or achiral molecules that contain stereocenters. Meso compounds and their mirror images are not stereoisomers, since they are identical.
Optical activity - The ability of chiral substances to rotate the plane of polarized light by a specific angle.
Dextrorotatory - Ability of chiral substances to rotate the plane of polarized light to the right.
Levorotatory - Ability of chiral substances to rotate the plane of polarized light to the left.
Specific rotation - The measured angle of rotation of polarized light by a pure chiral sample under specified standard conditions (refer to textbook for a description of these).
Racemic mixture, racemic modification, or racemate - A mixture consisting of equal amounts of enantiomers. A racemic mixture exhibits no optical activity because the activities of the individual enantiomers are equal and opposite in value, therby canceling each other out.
Optical purity - The difference in percent between two enantiomers present in a mixture in unequal amounts. For example, if a mixture contains 75% of one enantiomer and 25% of the other, the optical purity is 75-25 = 50%.
Absolute configuration - A description of the precise 3-dimensional topography of the molecule.
Relative configuration - A description of the 3-dimensional topography of the molecule relative to an arbitrary standard. Absolute and relative configurations may or may not coincide
4. RELATIONSHIPS BETWEEN CHIRAL CENTERS AND CHIRAL MOLECULES - The term chiral center refers to an atom in the molecular structure. The term chiral molecule refers to the entire molecule.
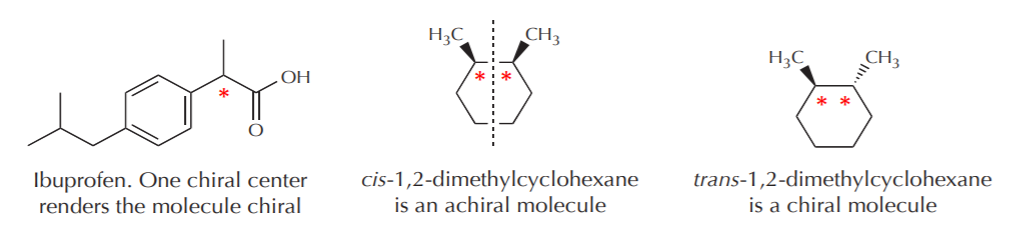
The presence of one chiral center renders the entire molecule chiral. The presence of two or more chiral centers may or may not result in the molecule being chiral. In the examples given below the chiral centers are indicated with an asterisk. The vertical broken line represents a plane of symmetry.
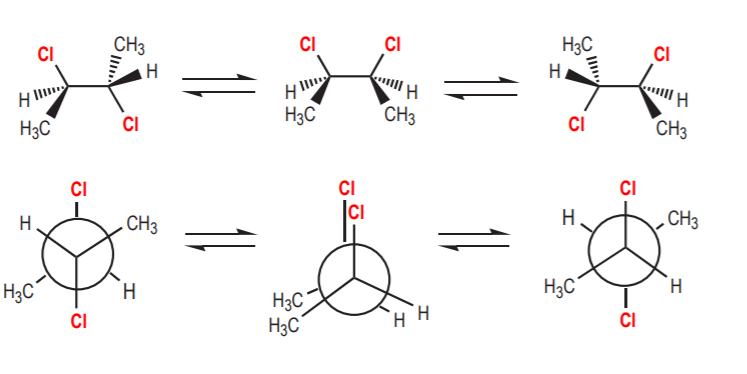
5. RELATIONSHIPS BETWEEN CONFORMATIONS AND CHIRALITY - The primary criterion to determine molecular chirality is the absence of any symmetry elements. However, some achiral molecules have chiral conformations. For example the chair conformations of 1,2-disubstituted cyclohexanes are chiral, yet the molecule as a whole is considered achiral. On the whole, we can apply the following criteria.
a) If the contributing conformations average out to an achiral conformation, then the molecule is considered achiral. Such molecules do not show optical activity. In the case of 1,2-disubstituted cyclohexanes the two most stable conformations are chiral. If we could freeze and isolate one of them, it would exhibit optical activity. But because they are mirror images in equilibrium, their optical activities cancel out and the sample is optically inactive. A similar example is illustrated by the conformations of (2R,3S)-1,2-dichlorobutane, which again is achiral, even though some of its conformations are chiral.

(2R,3S)-2,3-dichlorobutane
b) If a chiral conformation prevails over the others, then the molecule is considered chiral and it will show optical activity. The most common situations of this type involve molecules which are locked up into a chiral conformation due to steric interactions that impede free rotation around sigma bonds. In the example shown below, the two benzene rings cannot be coplanar because the steric interactions between the methyl and chlorine groups are too severe. The molecule is locked up in a conformation that has no symmetry, therefore it is chiral. Also notice that the molecule does not have any chiral centers. Its chirality is strictly due to a conformational effect.