3.4: Configurational stereoisomerism
- Page ID
- 527173
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)What is a configurational isomer?
Isomers are molecules or species that have the same molecular formula but different arrangements of atoms in their structure. If the different arrangement of atoms is due to a different sequence of atoms, these are constitutional isomers. If the sequence of atoms is the same, but their orientation in space is different, they are stereoisomers. If the different orientation of atoms in stereoisomers is a result of free rotation around single bonds, they are conformational isomers. For example, anti and gauche-forms of butane, shown on the left margin, are conformational isomers that interconvert by rotating parts of the molecule around single bonds relative to other parts. On the other hand, if different orientation of stereoisomers is a permanent geometry that requires making and re-making some bonds for their interconversion, they are configurational isomers. For example, cis- and trans-but-2-ene, shown on the right margin, are configurational isomers.
A molecule's permanent geometry, which results from the spatial arrangement of its bonds, is called its configuration.
An atom within a molecule bearing groups such that interchanging any two of them leads to a stereoisomer of the original molecule is referred to as a stereogenic center.
For example, both double-bonded carbons \(\ce{C=C}\) in but-2-ene, shown in the figure on the right margin, are stereogenic centers, interchanging \(\ce{-H}\) with \(\ce{-CH3}\) on any one of them converts cis- to trans isomer and vice versa.
Types of configurational isomers
Every object, including molecular structure, has its reflection when it is placed against a mirror, called its mirror image. Suppose the object and its mirror image are real. In that case, they are either identical, i.e., they superpose on each other thoroughly after rotating the entire object or molecule around some axes, or they are non-superposable mirror images. Stereoisomers are either non-superimposable mirror images of each other, known as enantiomers, or they are not mirror images of each other, referred to as diastereomers. This difference between identical structures, enantiomers, and diastereomers is illustrated in Figure \(\PageIndex{1}\).
If the stereoisomers are non-superposable mirror images of each other, they are enantiomers; otherwise, they are diastereomers.
Chirality
Chirality is a property related to a superposable relationship between an object and another object that would be like its mirror image. Mirrors reflect light and produce an inverted, or imaginary, picture of the object seen behind the mirror. For example, the water surface of Mirror Lake reflects the beautiful scenery of Mount Hood, as shown in the figure below (Copyright: Oregon's Mt. Hood Territory, Public domain, via Wikimedia Commons)
The geometric property of a rigid object, including molecules, that prevents it from being superposable on its mirror image is referred to as chirality. An object, including a molecule, that is not superposable on its mirror image is referred to as chiral. An object or a molecule that is superposable on its mirror image is referred to as achiral.
Figure \(\PageIndex{2}\) shows some examples of chiral objects. Chirality is usually associated with life. For example, human eyes, ears, hands, and feet are chiral objects. Chiral molecules are also usually biochemicals. For example, amino acids that constitute proteins, DNA molecules, carbohydrates, etc., are generally chiral molecules.
Left and right hands,
clockwise and counterclockwise springs,
left- and right-handed shells of sea snails, and
left and right shoes.
Chiral objects do not have a plane of symmetry and do not have a point of symmetry. Achiral objects have a plane of symmetry and/or a point of symmetry.
A plane of symmetry is a flat surface that divides the object into two halves, such that one half is a mirror image of the other.
For example, a cup of coffee, shown on the right margin, is an achiral object with a plane of symmetry, shown as a red line frame overlaid on the picture.
A point of symmetry is a point in the middle of an object such that if any feature of the object is reflected, an identical feature will found on the opposite side of the point at the same distance.
For example, the point in the center of the plate, as shown in the left margin, through which red lines are crossing, is its point of symmetry. A sphere has a point of symmetry at its center and also has unlimited symmetry planes. Figure \(\PageIndex{3}\) shows some examples of achiral objects.
A baseball, 
a pencil, 
a shovel, 
a fork, a plate, a knife, a spoon, and
a sphere.Chirality at the molecular level
Like objects, molecules are either achiral when their mirror image superposes on them or chiral when their mirror image does not superpose on them. For example, molecules #1, #2, #3, #4, and #5 in Figure \(\PageIndex{1}\) are achiral, having superposable mirror images, while molecule#6 is chiral as its mirror image is non-superposable on it.
Often, achiral molecules have one or more planes of symmetry that divide them into equal halves, as illustrated in Figure \(\PageIndex{4}\). The figure on the right margin illustrates formaldehyde \(\ce{H2C=O}\) that is a planer molecule having two-fold axis of symmetry \(C_2\) and \(\sigma_{v}\) and \(\sigma_{v'}\) are two planes of symmetry: one is in the plane of the molecule, cutting every atom in two halves and the other of dotted liens is perpendicular to the plane of the molecule, cutting it in two halves along \(\ce{C=O}\) bond (Copyright: Public domain).
1) Achiral
2) Achiral
3) Achiral
4) Achiral
5) Achiral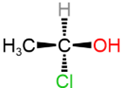
6) Chiral
The presence of a plane of symmetry is sufficient to define a molecule as achiral; its absence usually means the molecule is chiral, but not necessarily always. There are a few exceptions where a molecule has no plane of symmetry, but it is still achiral due to the presence of a point of symmetry. For example, the molecule shown in the left margin, ((3R,6S)-1,3,4,6-tetramethylpiperazine-2,5-dione), does not have a plane of symmetry; however, it is achiral because it possesses a point of symmetry.
Chirality center
An atom holding a set of ligands (groups) in a spatial arrangement that is not superposable on its mirror image is referred to as a chirality center. A carbon that is a chirality center is also called an asymmetric carbon atom.
For example, \(\ce{N^{+}}\) in the figure on the left margin and \(\ce{C}\) in the figure on the right margin are chirality centers. The (\ce{C}\) in the figure on the right margin is also an asymmetric carbon atom.
Identifying chirality centers
Often, the presence of an asymmetric \(\ce{C}\) is the cause of chirality of the molecule. \(\ce{C}\) chirality centers in a molecule can be identified by the following rules.
- An \(sp\ce{C}\) or \(sp^2 \ce{C}\) is not a chirality center. For example, central \(\ce{C}\) in example#1 and #2 in Figure \(\PageIndex{4}\) are not chirality centers.
- An \(sp^3 \ce{C}\) with two or more same substituents is not a chirality center. For example, central \(\ce{C}\) in example#3, #4, and #5 in Figure \(\PageIndex{4}\) having two or more \(\ce{H's}\) are not chirality centers.
- An \(sp^3 \ce{C}\) with four different substituents is a chirality center. For example, central \(\ce{C}\) in example#6 in in Figure \(\PageIndex{4}\) is a chirality center.
When substituents contain more than one atom, first compare the atoms directly bonded to the atom under consideration, then the atoms two bonds away, then the atoms three bonds away, until the first point of difference is reached. For example, the first structure in Figure \(\PageIndex{5}\) has \(\ce{H}\), \(\ce{O}\), \(\ce{C}\), and \(\ce{C}\) at one bond away from the \(\ce{C}\) highlighted yellow. The last two substituents have \(\ce{C}\), \(\ce{H}\), and \(\ce{H}\), i.e., the same two bonds away. First difference is at three bonds away \(\ce{C}\), \(\ce{H}\), \(\ce{H}\) versus \(\ce{C}\), \(\ce{C}\), \(\ce{H}\), as highlighted red. So the four substitutions are different, making the \(\ce{C}\) highlighted yellow a chirality center. If all atoms are compared this way and no difference is found, the two substituents are the same, and the atom under consideration is not a chirality center.
One chirality center: yellow.
No chirality center.
Two chirality centers: yellow and red.
Eight chirality centers are labeled by an asterisk.If the atom under consideration is part of a cyclic chain, two substituents are the parts of the chain on the two sides of the atom. As usual, compare the atoms directly bonded to the atom under consideration, then two bonds away, then three bonds away, and so on, until the first point of difference is found, or the group of atoms common to both sides is reached, meaning the two sides of the cyclic structure are the same substituent. For example, \(\ce{C}\) highlighted yellow in the second structure in Figure \(\PageIndex{5}\) as \(\ce{-Cl}\), \(\ce{-H}\) and two \(\ce{C's}\) of the cyclic structure at one bond away. The atoms two bonds away are \(\ce{C}\), \(\ce{H}\), \(\ce{H}\), the same one on both sides, and the atoms three bonds away are common to both sides. Therefore, the \(\ce{C}\) highlighted yellow in this structure is not a chirality center. The \(\ce{C}\) highlighted yellow in the third structure in Figure \(\PageIndex{5}\) is chiral, having four different substituents. The first difference in the two sides of the cyclic structure is at two bonds away, i.e., \(\ce{C}\), \(\ce{H}\), \(\ce{H}\) versus \(\ce{C}\), \(\ce{C}\), \(\ce{H}\), as shown in the figure. The \(\ce{C}\) highlighted red in this structure is the second chirality center, for which the first difference in the two sides of the cyclic structure is at three bonds away, i.e., \(\ce{C}\), \(\ce{H}\), \(\ce{H}\) versus \(\ce{Cl}\), \(\ce{C}\), \(\ce{H}\).
Biochemicals often have more than one chirality center. They are usually labeled with an asterisk if needed. For example, cholesterol, the fourth structure in Figure \(\PageIndex{5}\), has eight chirality centers labeled with an asterisk. Note that two of the \(\ce{H's}\) on \(\ce{C's}\) are shown in this skeletal structure as they were needed to show the correct configuration of the \(\ce{C's}\). The rest of the \(\ce{H's}\) on \(\ce{C's}\) are implicit, as usual.
Representing the configuration of a chirality center
A sp3-hybridized atom is tetrahedral, i.e., four \(\sigma\)-bonds as two V's of 109.5 internal angle joined perpendicular to each other at vortexes, e.g., methane \(\ce{CH4}\) modeled as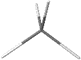 
. Tetrahedral geometry is a 3D geometry typically represented by perspective drawings or Fisher projections, which are described in the following sections.
Perspective drawing
Since the tetrahedral geometry is two V's perpendicular to each other, one V is placed in the plane of the screen (or page) and represented by solid lines. The other V is represented by a solid wedge, indicating the bond emerging from the screen towards the viewer, and a hashed wedge, representing the bond extending beyond the screen away from the viewer. When the central atom is a chirality center, two configurations of enantiomers are possible, as illustrated in the figure on the right margin for two enantiomers of 2-chlorobutane. The view angle is from the direction of the top-left corner. The V in the plane of the screen appears larger, and the other appears smaller. Typically, the solid wedge is positioned closer to the viewer than the hashed wedge.
If the configuration of two or more connected \(\ce{C's}\) needs to be shown, the V's in the plane of the screen are usually drawn pointing downwards or upwards, making a zig-zag line. For example, four stereoisomers of 3-chlorobutan-2-ol, which have two chirality centers, are shown in Figure \(\PageIndex{6}\). Semi-condensed formulas show all atoms, but skeletal formulas do not show \(\ce{C's}\) and \(\ce{H's}\), except when it is necessary to show the configuration of the chirality center, as illustrated in In the case of skeletal formulas, \(\ce{C's}\) and \(\ce{H's}\) are not shown. However, the configuration is still readable correctly from the bonds shown, as illustrated in Figure \(\PageIndex{6}\).
Fisher projections
Fisher projections represent the configuration as a 2D projection of the molecule, with four bonds arranged in the shape of a cross. The following steps and Figure \(\PageIndex{7}\) (left) illustrate how to draw a Fisher projection from a perspective drawing.
- Look at the chirality center such that the bonds extending towards the viewer are placed horizontally and the bonds extending away from the viewer are drawn vertically.
- Replace solid and hashed wedges with straight lines, assuming the horizontal lines are bonds forward and the vertical lines are bonds backward.
The steps are applied to an example of alanine enantiomers shown in Figure \(\PageIndex{7}\) (right)
Visualization of the process.
Examples: Alanine enantiomers
When there is more than one chirality center, the following steps convert the skeletal drawing into the Fischer projection.
- The \(\ce{C}\)-backbone is oriented from horizontal to vertical by a 90\(^o\) rotation of the entire molecule. The most oxidized carbon is usually placed at or near the top.
- Part of the molecule is rotated 180\(^o\) around \(\ce{C-C}\) single bond between two chirality centers, resulting in a semi-cyclic conformation.
- If there are more than two chirality centers, this step is repeated for the third chirality center, then for the fourth, and so on.
- The chirality centers are viewed from the edge-on so that the bonds of the \(\ce{C}\)-backbone are pointing away from the viewer and the bonds to the two substituents are horizontal, pointing towards the viewer. This step is repeated for each chirality center, as illustrated in Figure \(\PageIndex{8}\).
