Learning Objective
- recognize the relationships between constitutional (structural) isomers, conformational isomers, and geometric isomers
Isomers
Isomers always have the same chemical formula. When the chemical formulae are different, then the compounds are completely different. Important information can be gained from the chemical formulas when comparing compounds.
Structural (constitutional) isomers have the same molecular formula but a different bonding arrangement among the atoms. Stereoisomers have identical molecular formulas and arrangements of atoms. They differ from each other only in the spatial orientation of groups in the molecule. For organic chemistry, there are several types of stereoisomers: enantiomers, diasteriomers, geometric isomers, and conformers. These stereoisomers will be introduced and explained throughout several chapters.
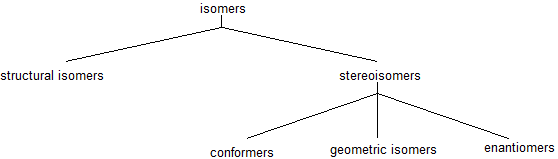
Structural (Constitutional) Isomers
Because carbon forms four bonds, there can be multiple ways to form molecules that follow the octet rule. Even with only four carbon atoms, there are two possible structures for the carbon backbone. The carbon atoms can be bonded to make a four carbon chain (butane) or there can be a one carbon branch from a three carbon chain (2-methylpropane). Butane and 2-methylpropane are structural isomers because they both have the chemical formula C4H10.

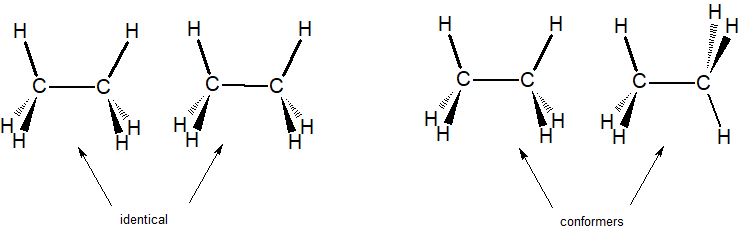
Identical vs Conformer
The rotation about single bonds creates dynamic molecules. When drawing and discussing molecules, it is important to be aware that our drawing are static while the molecule themselves are rotating. Although there are seven sigma bonds in the ethane molecule, rotation about the six carbon-hydrogen bonds does not result in any change in the shape of the molecule because the hydrogen atoms are essentially spherical. Rotation about the carbon-carbon bond, however, results in many different possible molecular conformations. Conformers are the simplest example of stereoisomerism.

Identical compounds are the same compound shown with ALL atoms in the same spatial orientation.
Conformers are the same compound shown with different rotations about single bonds.
In the example below, we can compare two identical structures for ethane with two conformers of ethane.
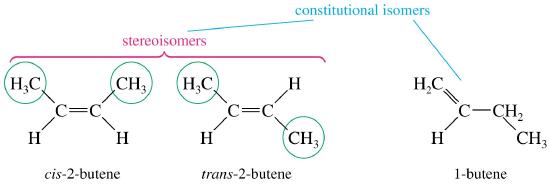
Geometric Isomers - an example of stereoisomerism
The rigidity of the pi bonds in double bonds can create geometric isomerism. Without rotation, there are two different orientations possible across the carbon-carbon double bond (C=C). The rigidity of the double bond creates a line of reference for spatial orientation. The prefixes cis and trans are used to distinguish between geometric isomers. The cis-stereoisomer has both non-hydrogen atoms on the same side of the double bond. Whereas, the trans-stereoisomer has the non-hydrogen atoms across the double bond. In the same way, we cross the ocean an a trans-Atlantic journey. This small difference may seem insignificant, but geometric isomers are different chemical compounds with different physical properties as shown in the example below.

For now, it is important to distinguish between structural differences and spatial differences when comparing compounds. In the future, we will look more closely at isomerism.
Example
Let's look ate the bond-line structures below and determine the relationships between the following pairs of compounds: identical, conformers, structural isomers, geometric isomers, or completely different compounds.
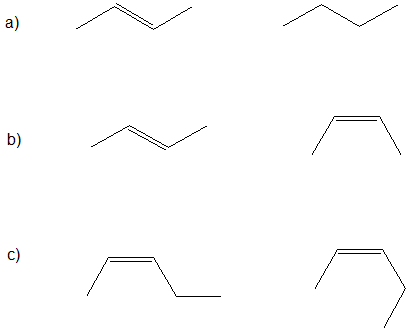
The first important step (that is often skipped) is to determine the chemical formula of each compound. If the chemical formulas are different, then the compounds are completely different and there is NO isomeric relationship. If the chemical formulas are the same, then we identify the difference between to the compounds to determine their relatioship. If there are structural differences in the bonding patterns, then the compounds are constitutional (structural isomers). If the compounds have the same structural connections, but the spatial orientations are different, then the compounds are stereoisomers. For now, the possible stereoisomers are conformers showing the same compound with different carbon-carbon single bond rotations or geometric isomers of compounds with different orientations at the carbon-carbon double bonds.
Applying the logic above to our example, we determine the following.
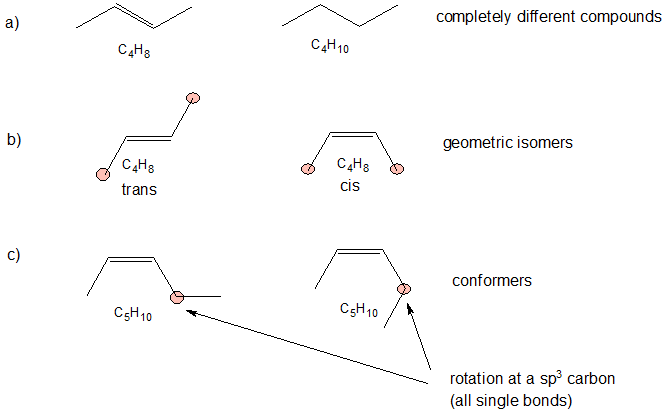
Exercise
1. What is the relationship between the following pairs of compounds: identical, conformers, structural isomers, geometric isomers, or completely different compounds?
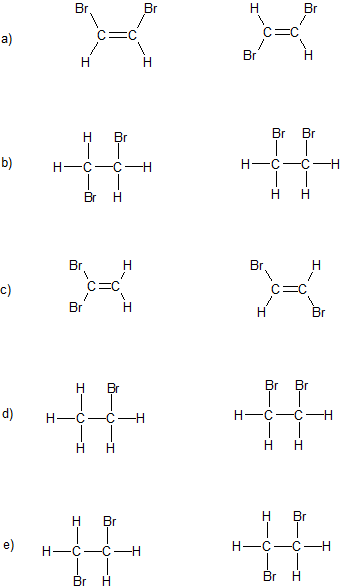
- Answer
-
1.
a) geometric isomers
b) conformers
c) structural isomers
d) completely different compounds
e) identical










