17.5: Aromaticity and Huckel's Rule
- Page ID
- 45557
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In 1931, German chemist and physicist Erich Hückel proposed a theory to help determine if a planar ring molecule would have aromatic properties. His rule states that if a cyclic, planar molecule has 4n+2 \(π\) electrons, it is considered aromatic. This rule would come to be known as Hückel's Rule.
Huckel's Rule: Aromatic, Antiaromatic, and Nonaromatic
Huckel's Rule is a set of algorithms that combine the number of \(\pi\) electrons (\(N\)) and the physical structure of the ring system to determine whether the molecule is aromatic, antiaromatic, or nonaromatic.
The number of \(\pi\) electrons in an aromatic system can be determined by the following algorithm:
\[N = 4n +2\]
where \(n\) is an integer.
The number of \(\pi\) electrons in an antiaromatic system can be determined by the following algorithm:
\[N = 4n\]
where \(n\) is an integer.
If a compound does not have a continuous ring of conjugated p orbitals in a planar conformation, then it is nonaromatic.
Huckel's Rule is a useful first step in evaluating the potential for a ringed molecule to be aromatic. The planar requirement of the ring may require further investigation.
Four Criteria for Aromaticity
When deciding if a compound is aromatic, go through the following checklist. If the compound does not meet all the following criteria, it is likely not aromatic.
- The molecule is cyclic (a ring of atoms)
- The molecule is planar (all atoms in the molecule lie in the same plane)
- The molecule is fully conjugated (p orbitals at every atom in the ring)
- The molecule has 4n+2 \(π\) electrons (n=0 or any positive integer)
Why 4n+2 \(\pi\) Electrons?
According to Hückel's Molecular Orbital Theory, a compound is particularly stable if all of its bonding molecular orbitals are filled with paired electrons. This is true of aromatic compounds, meaning they are quite stable. With aromatic compounds, 2 electrons fill the lowest energy molecular orbital, and 4 electrons fill each subsequent energy level (the number of subsequent energy levels is denoted by n), leaving all bonding orbitals filled and no anti-bonding orbitals occupied. This gives a total of 4n+2 \(\pi\) electrons. You can see how this works with the molecular orbital diagram for the aromatic compound, benzene, below. Benzene has 6 \(\pi\) electrons. Its first 2 \(\pi\) electrons fill the lowest energy orbital, and it has 4 \(\pi\) electrons remaining. These 4 fill in the orbitals of the succeeding energy level. Notice how all of its bonding orbitals are filled, but none of the anti-bonding orbitals have any electrons.
.jpg?revision=1&size=bestfit&width=317&height=292)
To apply the 4n+2 rule, first count the number of \(\pi\) electrons in the molecule. Then, set this number equal to \(4n+2\) and solve for \(n\). If is 0 or any positive integer (1, 2, 3,...), the rule has been met. For example, benzene has six \(\pi\) electrons:
\[\begin{align*} 4n + 2 &= 6 \\ 4n &= 4 \\ n &= 1 \end{align*}\]
For benzene, we find that \(n=1\), which is a positive integer, so the rule is met.
How Can You Tell Which Electrons are \(\pi\) Electrons?
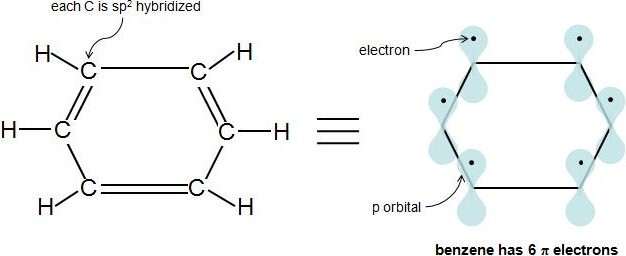
Perhaps the toughest part of Hückel's Rule is figuring out which electrons in the compound are actually \(\pi\) electrons. Once this is figured out, the rule is quite straightforward. \(\pi\) electrons lie in p orbitals and \(sp^2\) hybridized atoms have 1 p orbital each. So if every carbon atom in the cyclic compound is \(sp^2\) hybridized, this means the molecule is fully conjugated (has 1 p orbital at each atom), and the electrons in these p orbitals are the \(\pi\) electrons. A simple way to know if an atom is \(sp^2\) hybridized is to see if it has 3 attached atoms and no lone pairs of electrons. This video provides a very nice tutorial on how to determine an atom's hybridization. In a cyclic hydrocarbon compound with alternating single and double bonds, each carbon is attached to 1 hydrogen and 2 other carbons. Therefore, each carbon is \(sp^2\) hybridized and has a p orbital. Let's look at our previous example, benzene:
Each double bond (π bond) always contributes 2 \(\pi\) electrons. Benzene has 3 double bonds, so it has 6 \(\pi\) electrons.
Aromatic Ions
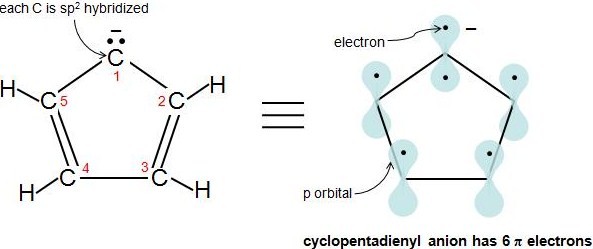
Hückel's Rule also applies to ions. As long as a compound has 4n+2 \(\pi\) electrons, it does not matter if the molecule is neutral or has a charge. For example, cyclopentadienyl anion is an aromatic ion. How do we know that it is fully conjugated? That is, how do we know that each atom in this molecule has 1 p orbital? Let's look at the following figure. Carbons 2-5 are sp2 hybridized because they have 3 attached atoms and have no lone electron pairs. What about carbon 1? Another simple rule to determine if an atom is sp2 hybridized is if an atom has 1 or more lone pairs and is attached to an sp2 hybridized atom, then that atom is sp2 hybridized also. This video explains the rule very clearly. Therefore, carbon 1 has a p orbital. Cyclopentadienyl anion has 6 \(\pi\) electrons and fulfills the 4n+2 rule.
Heterocyclic Aromatic Compounds
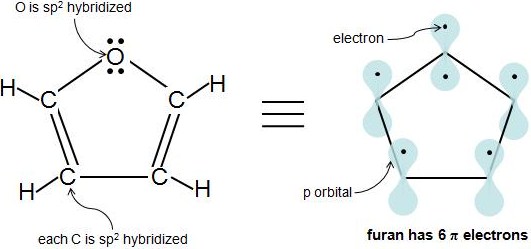
So far, you have encountered many carbon homocyclic rings, but compounds with elements other than carbon in the ring can also be aromatic, as long as they fulfill the criteria for aromaticity. These molecules are called heterocyclic compounds because they contain 1 or more different atoms other than carbon in the ring. A common example is furan, which contains an oxygen atom. We know that all carbons in furan are sp2 hybridized. But is the oxygen atom sp2 hybridized? The oxygen has at least 1 lone electron pair and is attached to an sp2 hybridized atom, so it is sp2 hybridized as well. Notice how oxygen has 2 lone pairs of electrons. How many of those electrons are \(\pi\) electrons? An sp2 hybridized atom only has 1 p orbital, which can only hold 2 electrons, so we know that 1 electron pair is in the p orbital, while the other pair is in an sp2 orbital. So, only 1 of oxygen's 2 lone electron pairs are \(\pi\) electrons. Furan has 6 \(\pi\) electrons and fulfills the 4n+2 rule.
A Common Misconception
A very common misconception is that hybridization can be used to predict the geometry, or that hybridization somehow involves an energy cost associated with 'promoting' electrons into the hybrid orbitals. This is entirely wrong. Hybridization is always determined by geometry. You can only assign hybridization states to an atom if you already know its geometry, based on some experimental or theoretical evidence. The geometry of the oxygen in furan is trigonal planar and therefore the hybridization must be \(sp^2\).
The specific rule is that if you have an \(sp^2\) conjugated system, the lone pair will be involved if it makes the system more stable. In this case, conferring Hückel \(4n+2\) aromaticity. For furan with two lone pairs on the oxygen atom, if we count electrons from the carbon atoms, we have 4 (one per carbon). So adding two electrons from one of the lone pairs will give 6 = 4(1)+2, so Hückel rule is applicable and furan is aromatic.
Exercise
3. Using the criteria for aromaticity, determine if the following molecules are aromatic:
- Answer
-
3.
Cpd 1: Aromatic - only 1 of S's lone pairs counts as \(\pi\) electrons, so there are 6 \(\pi\) electrons, n=1 Not aromatic - not fully conjugated, top C is sp3 hybridized
Cpd 2: Not aromatic - top C is sp2 hybridized, but there are 4 \(\pi\) electrons, n=1/2
Cpd 3: Aromatic - N is using its 1 p orbital for the electrons in the double bond, so its lone pair of electrons are not \(\pi\) electrons, there are 6 \(\pi\) electrons, n=1
Cpd 4: Aromatic - there are 6 \(\pi\) electrons, n=1
Cpd 5: Aromatic - there are 6 \(\pi\) electrons, n=1 because the N assumes sp2 hybridization.
Cpd 6: Not aromatic - all atoms are sp2 hybridized, but only 1 of S's lone pairs counts as \(\pi\) electrons, so there 8 \(\pi\) electrons, n=1.5
Cpd 7: Not aromatic - there are 4 \(\pi\) electrons, n=1/2
Cpd 8: Aromatic - only 1 of N's lone pairs counts as \(\pi\) electrons, so there are 6 \(\pi\) electrons, n=1
Cpd 9: Not aromatic - not fully conjugated, top C is sp3 hybridized
Cpd 10: Aromatic - O is using its 1 p orbital for the elections in the double bond, so its lone pair of electrons are not \(\pi\) electrons, there are 6 \(\pi\) electrons, n=1
References
- Vollhardt, Peter, and Neil E. Schore. Organic Chemistry: Structure and Function. 5th ed. New York: W. H. Freeman & Company, 2007.
- Berson, Jerome. Chemical Creativity: Ideas from the Work of Woodward, Hückel, Meerwein, and Others. New York: Wiley-VCH, 1999.
- Badger, G.M. Aromatic Character and Aromaticity. London, England: Cambridge University Press, 1969.
- Lewis, David and David Peters. Facts and Theories of Aromaticity. London, England: Macmillan Press, 1975.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
- bon and Geoff Hutchison from Chemistry StackExchange


.jpg?revision=1)
.jpg?revision=1)
.jpg?revision=1)
.jpg?revision=1&size=bestfit&width=440&height=181)