14.1: Conjugation

Allylic Carbocation

Conjugation occurs when p orbital on three or more adjacent atoms can overlap Conjugation tends to stabilize molecules

Allylic carbocations are a common conjugated system.

The positive charge of a carbocation is contained in a P orbital of a sp² hybridized carbon. This allows for overlap with double bonds. The positive charge is more stable because it is spread over 2 carbons.

Molecular Orbitals of an Allylic Carbocation

The stability of the carbocation of propene is due to a conjugated π electron system. A "double bond" doesn't really exist. Instead, it is a group of 3 adjacent, overlapping, non-hybridized p orbitals we call a conjugated π electron system. You can clearly see the interactions between all three of the p orbitals from the three carbons resulting in a really stable cation. It all comes down to where the location of the electron-deficient carbon is.

Molecular orbital descriptions can explain allylic stability in yet another way using 2-propenyl. Fig.6

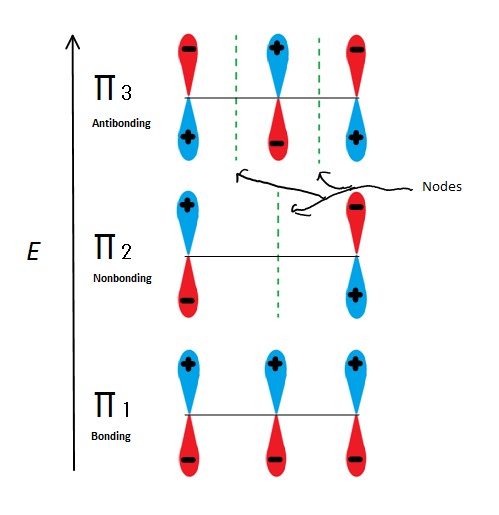
Fig.6 Shows the 3 possible Molecular orbitals of 2-propenyl

If we just take the π molecular orbital and not any of the s, we get three of them. π₁ is bonding with no nodes, π₂ is nonbonding (In other words, the same energy as a regular p-orbital) with a node, and π₃ is antibonding with 2 nodes (none of the orbitals are interacting). The first two electrons will go into the π₁ molecular orbital, regardless of whether it is a cation, radical, or anion. If it is a radical or anion, the next electron goes into the π₂ molecular orbital. The last anion electron goes into the nonbonding orbital also. So no matter what kind of carbon center exists, no electron will ever go into the antibonding orbital.

The Bonding orbitals are the lowest energy orbitals and are favorable, which is why they are filled first. Even though the nonbonding orbitals can be filled, the overall energy of the system is still lower and more stable due to the filled bonding molecular orbitals.

This figure also shows that π₂ is the only molecular orbital where the electrion differs, and it is also where a single node passes through the middle. Because of this, the charges of the molecule are mainly on the two terminal carbons and not the middle carbon.

This molecular orbital description can also illustrate the stability of allylic carbon centers in figure 7.

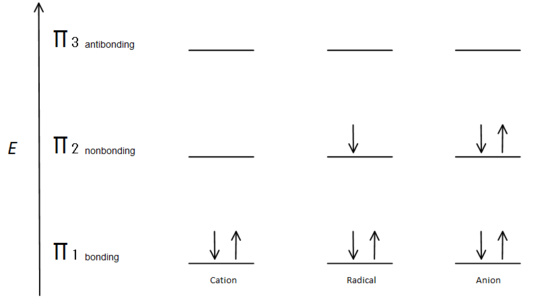
Fig.7 diagram showing how the electrons fill based on the Aufbau principle.

The π bonding orbital is lower in energy than the nonbonding p orbital. Since every carbon center shown has two electrons in the lower energy, bonding π orbitals, the energy of each system is lowered overall (and thus more stable), regardless of cation, radical, or anion.

1,3-Dienes

Conjugated double bonds are separated by a single bond. 1,3-dienes are an excellent example of a conjugated system. Each carbon in 1,3 dienes are sp² hybridized and therefore have one p orbital. The four p orbitals in 1,3-butadiene overlap to form a conjugated system.

Conjugated vs. Nonconjugated Dienes

Conjugated dienes are two double bonds separated by a single bond

Nonconjugated (Isolated) Dienes are two double bonds are separated by more than one single bond.

When using electrostatic potential maps, it is observed that the pi electron density overlap is closer together and delocalized in conjugated dienes, while in non conjugated dienes the pi electron density is located differently across the molecule. Since having more electron density delocalized makes the molecule more stable conjugated dienes are more stable than non conjugated

For example in 1,3-butadiene the carbons with the single bond are sp2 hybridized unlike in nonconjugated dienes where the carbons with single bonds are sp3 hybridized. This difference in hybridization shows that the conjugated dienes have more 's' character and draw in more of the pi electrons, thus making the single bond stronger and shorter than an ordinary alkane C-C bond (1.54Å).

Stability of Conjugated Dienes

Conjugated dienes are more stable than non conjugated dienes (both isolated and cumulated) due to factors such as delocalization of charge through resonance and hybridization energy. This can also explain why allylic radicals are much more stable than secondary or even tertiary carbocations. This is all due to the positioning of the pi orbitals and ability for overlap to occur to strengthen the single bond between the two double bonds.

The resonance structure shown below gives a good understanding of how the charge is delocalized across the four carbons in this conjugated diene. This delocalization of charges stablizes the conjugated diene:

Along with resonance, hybridization energy effect the stability of the compound. For example in 1,3-butadiene the carbons with the single bond are sp2 hybridized unlike in nonconjugated dienes where the carbons with single bonds are sp3 hybridized. This difference in hybridization shows that the conjugated dienes have more 's' character and draw in more of the pi electrons, thus making the single bond stronger and shorter than an ordinary alkane C-C bond (1.54Å).

Molecular Orbitals of 1,3 Dienes

A molecular orbital model for 1,3-butadiene is shown below. Note that the lobes of the four p-orbital components in each pi-orbital are colored differently and carry a plus or minus sign. This distinction refers to different phases, defined by the mathematical wave equations for such orbitals. Regions in which adjacent orbital lobes undergo a phase change are called nodes. Orbital electron density is zero in such regions. Thus a single p-orbital has a node at the nucleus, and all the pi-orbitals shown here have a nodal plane that is defined by the atoms of the diene. This is the only nodal surface in the lowest energy pi-orbital, π₁. Higher energy pi-orbitals have an increasing number of nodes.

'

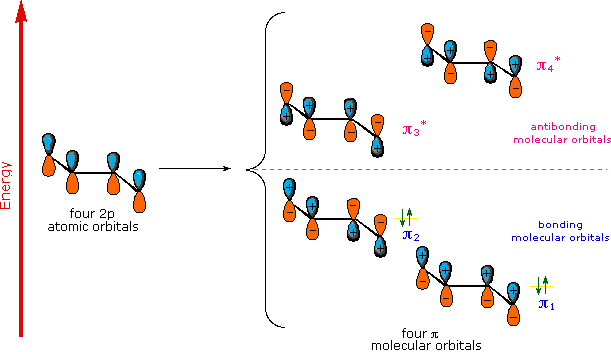Contributors

• William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

• Prof. Steven Farmer (Sonoma State University)

• Jim Clark (Chemguide.co.uk)

• Jeffrey Hu