5.11: Isomers—A Summary

Conformational Isomers

The C–C single bonds in ethane, propane, and other alkanes are formed by the overlap of an sp³ hybrid orbital on one carbon atom with an sp³ hybrid orbital on another carbon atom, forming a σ bond. Each sp³ hybrid orbital is cylindrically symmetrical (all cross-sections are circles), resulting in a carbon–carbon single bond that is also cylindrically symmetrical about the C–C axis. Because rotation about the carbon–carbon single bond can occur without changing the overlap of the sp³ hybrid orbitals, there is no significant electronic energy barrier to rotation. Consequently, many different arrangements of the atoms are possible, each corresponding to different degrees of rotation. Differences in three-dimensional structure resulting from rotation about a σ bond are called differences in conformation, and each different arrangement is called a conformational isomer (or conformer).

Structural Isomers

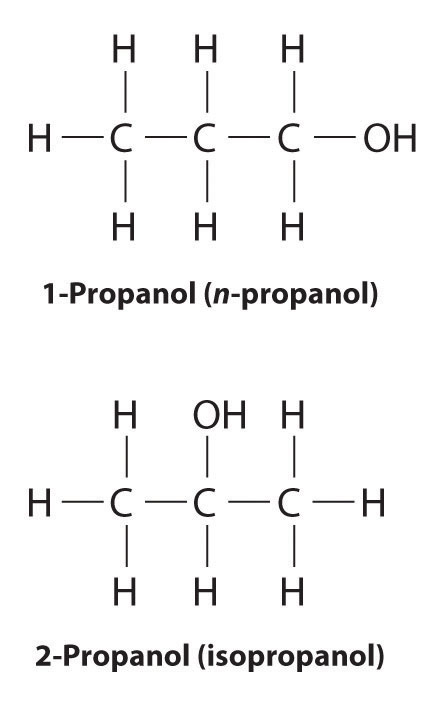
Unlike conformational isomers, which do not differ in connectivity, structural isomers differ in connectivity, as illustrated here for 1-propanol and 2-propanol. Although these two alcohols have the same molecular formula (C₃H₈O), the position of the –OH group differs, which leads to differences in their physical and chemical properties.

In the conversion of one structural isomer to another, at least one bond must be broken and reformed at a different position in the molecule. Consider, for example, the following five structures represented by the formula C₅H₁₂:

Of these structures, (a) and (d) represent the same compound, as do (b) and (c). No bonds have been broken and reformed; the molecules are simply rotated about a 180° vertical axis. Only three—n-pentane (a) and (d), 2-methylbutane (b) and (c), and 2,2-dimethylpropane (e)—are structural isomers. Because no bonds are broken in going from (a) to (d) or from (b) to (c), these alternative representations are not structural isomers. The three structural isomers—either (a) or (d), either (b) or (c), and (e)—have distinct physical and chemical properties.

Stereoisomers

Molecules with the same connectivity but different arrangements of the atoms in space are called stereoisomers. There are two types of stereoisomers: geometric and optical. Geometric isomers differ in the relative position(s) of substituents in a rigid molecule. Simple rotation about a C–C σ bond in an alkene, for example, cannot occur because of the presence of the π bond. The substituents are therefore rigidly locked into a particular spatial arrangement (part (a) in Figure 2.16. Thus a carbon–carbon multiple bond, or in some cases a ring, prevents one geometric isomer from being readily converted to the other. The members of an isomeric pair are identified as either cis or trans, and interconversion between the two forms requires breaking and reforming one or more bonds. Because their structural difference causes them to have different physical and chemical properties, cis and trans isomers are actually two distinct chemical compounds.

Note

Stereoisomers have the same connectivity but different arrangements of atoms in space.

Optical isomers are molecules whose structures are mirror images but cannot be superimposed on one another in any orientation. Optical isomers have identical physical properties, although their chemical properties may differ in asymmetric environments. Molecules that are nonsuperimposable mirror images of each other are said to be chiral (pronounced “ky-ral,” from the Greek cheir, meaning “hand”). Examples of some familiar chiral objects are your hands, feet, and ears. As shown in part (a) in Figure 5.11.1., your left and right hands are nonsuperimposable mirror images. (Try putting your right shoe on your left foot—it just doesn’t work.) An achiral object is one that can be superimposed on its mirror image, as shown by the superimposed flasks in part (b) in Figure 5.11.1..

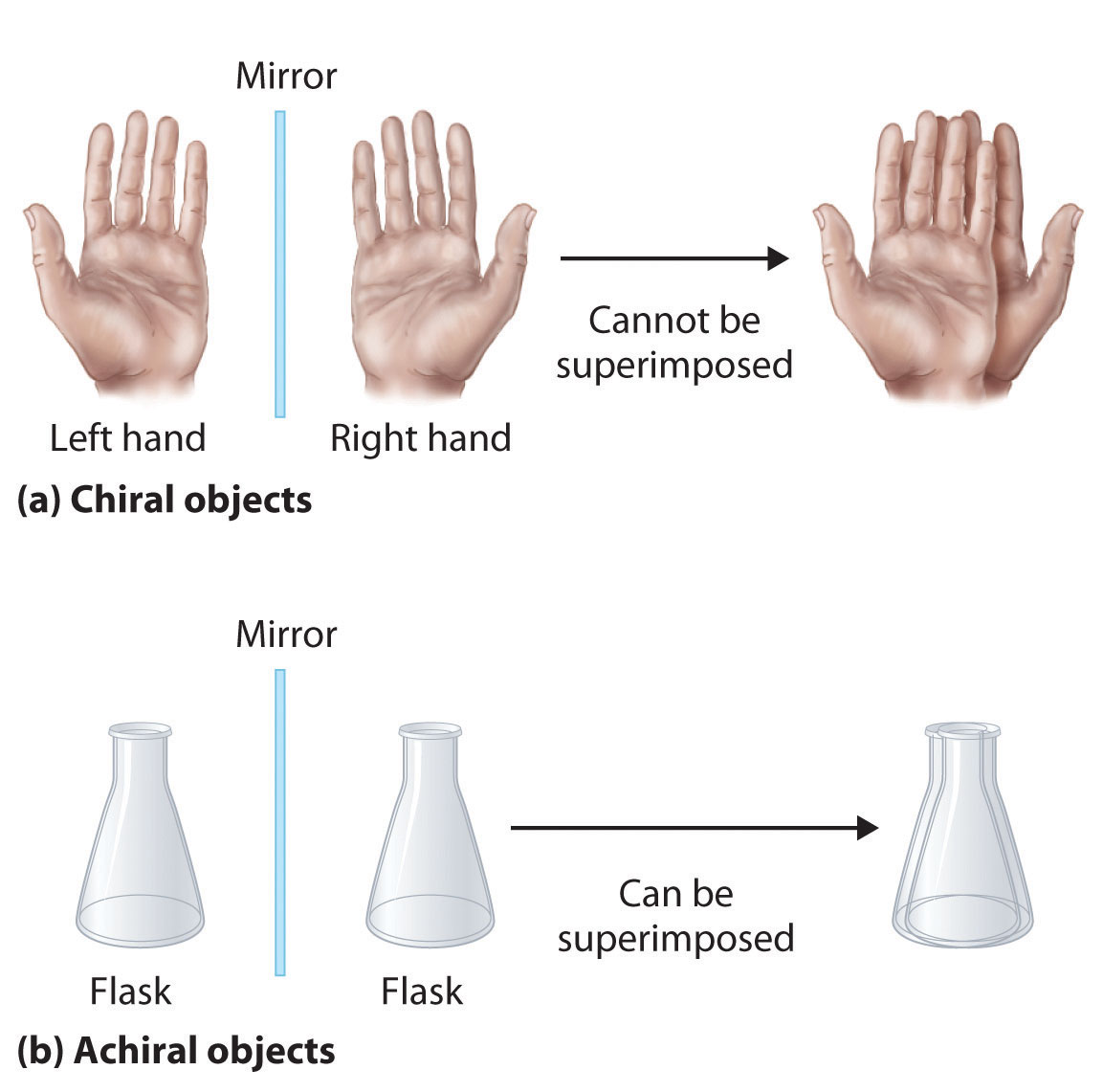
Figure 5.11.1: Chiral and Achiral Objects. (a) Objects that are nonsuperimposable mirror images of each other are chiral, such as the left and the right hand. (b) The unmarked flask is achiral because it can be superimposed on its mirror image.

Most chiral organic molecules have at least one carbon atom that is bonded to four different groups, as occurs in the bromochlorofluoromethane molecule shown in part (a) in Figure 5.11.2. This carbon, often designated by an asterisk in structural drawings, is called a chiral center or asymmetric carbon atom. If the bromine atom is replaced by another chlorine (part (b) in Figure 5.11.2), the molecule and its mirror image can now be superimposed by simple rotation. Thus the carbon is no longer a chiral center. Asymmetric carbon atoms are found in many naturally occurring molecules, such as lactic acid, which is present in milk and muscles, and nicotine, a component of tobacco. A molecule and its nonsuperimposable mirror image are called enantiomers (from the Greek enantiou, meaning “opposite”).

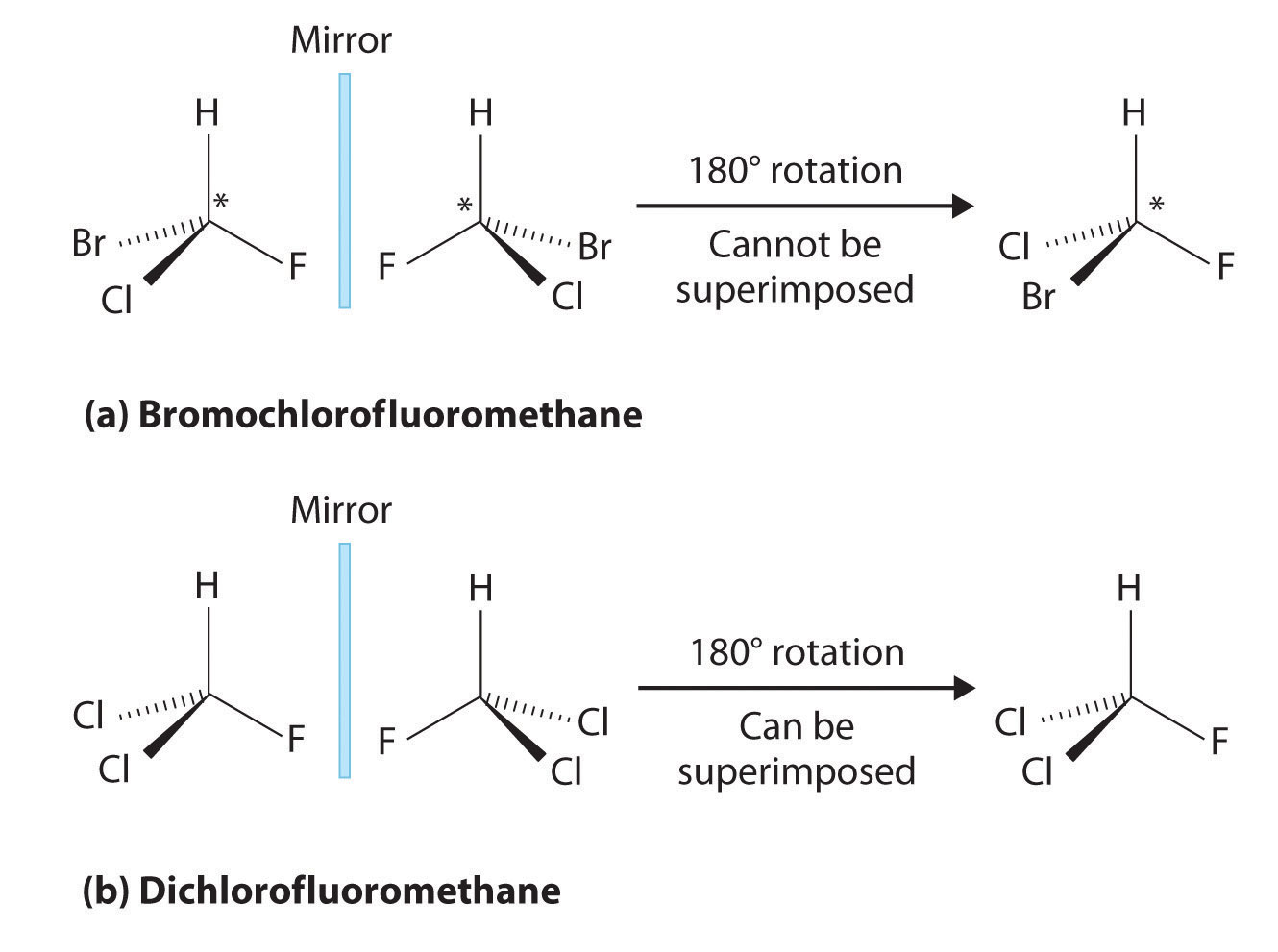
Figure 5.11.2: Comparison of Chiral and Achiral Molecules. (a) Bromochlorofluoromethane is a chiral molecule whose stereocenter is designated with an asterisk. Rotation of its mirror image does not generate the original structure. To superimpose the mirror images, bonds must be broken and reformed. (b) In contrast, dichlorofluoromethane and its mirror image can be rotated so they are superimposable.

Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

• Dan Chong