30.5: Sigmatropic Rearrangements
- Page ID
- 14227
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
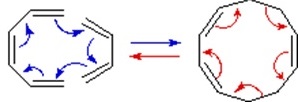
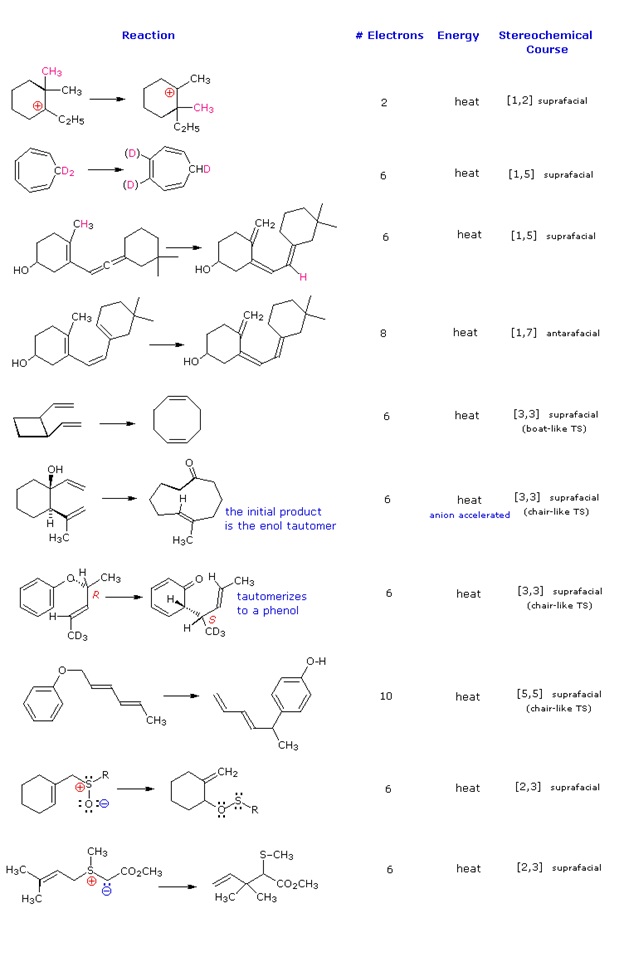
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Molecular rearrangements in which a σ-bonded atom or group, flanked by one or more π-electron systems, shifts to a new location with a corresponding reorganization of the π-bonds are called sigmatropic reactions. The total number of σ-bonds and π-bonds remain unchanged. These rearrangements are described by two numbers set in brackets, which refer to the relative distance (in atoms) each end of the σ-bond has moved, as illustrated by the first equation in the diagram below. The most common atom to undergo sigmatropic shifts is hydrogen or one of its isotopes. The second equation in the diagram shows a facile [1,5] hydrogen shift which converts a relatively unstable allene system into a conjugated triene. Note that this rearrangement, which involves the relocation of three pairs of bonding electrons, may be described by three curved arrows.
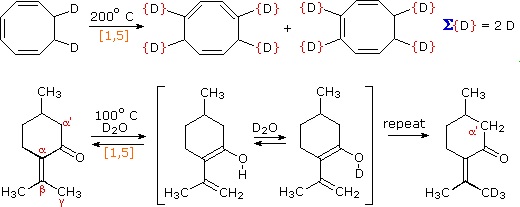
These reactions are particularly informative in that [1,3] hydrogen shifts are not observed. The reactant in the first equation is a deuterium labeled 1,3,5-cyclooctatriene. On heating, this compound equilibrates with its 1,3,6-triene isomer, and the two deuterium atoms are scrambled among the four locations noted. If [1,3] or [1,7] hydrogen shifts were taking place, the deuterium atoms would be distributed equally among all eight carbon atoms. On prolonged heating, or at higher temperatures these cyclooctatrienes undergo electrocyclic ring opening to 1,3,5,7-octatetraene and reclosure to vinyl-1,3-cyclohexadienes.
The second example shows another [1,5] hydrogen shift, from the proximal methyl group to the carbonyl oxygen atom. The resulting dienol rapidly exchanges OH for OD before the [1,5] shift reverses. In this manner the reactive methyl is soon converted to CD3. Since hydrogens alpha to a carbonyl group are known to undergo acid or base catalyzed exchange by way of enol intermediates, we might expect the α'-CH2 group to exchange as well. However, if care is taken to remove potential acid or base catalysts, the thermal [1,3] shift necessary for the exchange is found to be very slow.
Cope and Claisen rearrangements
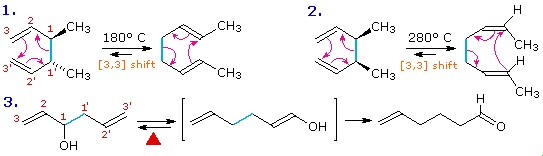
The [3,3] sigmatropic rearrangement of 1,5-dienes or allyl vinyl ethers, known respectively as the Cope and Claisen rearrangements, are among the most commonly used sigmatropic reactions. Three examples of the Cope rearrangement are shown in the following diagram. Reactions 1 and 2 (top row) demonstrate the stereospecificity of this reaction. The light blue σ-bond joins two allyl groups, oriented so their ends are near each other. Since each allyl segment is the locus of a [1,3] shift, the overall reaction is classified as a [3,3] rearrangement. The three pink colored curved arrows describe the redistribution of three bonding electron pairs in the course of this reversible rearrangement. The diene reactant in the third reaction is drawn in an extended conformation. This molecule must assume a coiled conformation (as above) before the [3,3] rearrangement can take place. The product of this rearrangement is an enol which immediately tautomerizes to its keto form. Such variants are termed the oxy-Cope rearrangement, and are useful because the reverse rearrangement is blocked by rapid ketonization. If the hydroxyl substituent is converted to an alkoxide salt, the activation energy of the rearrangement is lowered significantly.
The degenerate or self-replicating Cope rearrangement has been a fascinating subject of research. For examples .
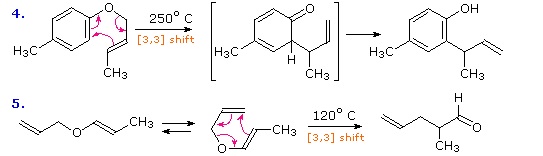
Two examples of the Claisen Rearrangement may be seen by clicking on the above diagram. Reaction 4 is the classic rearrangement of an allyl phenyl ether to an ortho-allyl phenol. The methyl substituent on the allyl moiety serves to demonstrate the bonding shift at that site. The initial cyclohexadienone product immediately tautomerizes to a phenol, regaining the stability of the aromatic ring. Reaction 5 is an aliphatic analog in which a vinyl group replaces the aromatic ring. In both cases three pairs of bonding electrons undergo a reorganization.
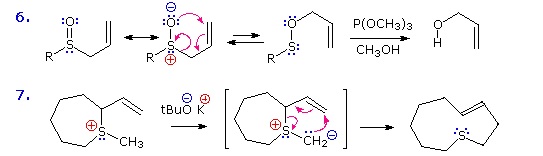
By clicking on the above diagram a second time two examples of [2,3] sigmatropic rearrangements will be displayed. The allylic sulfoxide in reaction 6 rearranges reversibly to a less stable sulfenate ester. The weak S-O bond may be reductively cleaved by trimethyl phosphite to an allylic alcohol and a thiol (not shown). Reaction 7 shows a similar rearrangement of a sulfur ylide to a cyclic sulfide. The [2,3]-Wittig rearrangement is yet another example.
Contributors
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

